Mikrohullámok mint állóhullámok, a fény közelítő sebessége

„Ha a húrnak egyik oldalán ennek bizonyos hányszoros része keresztrezgésekbe kerül, akkor onnan egy hullámsor kiindul, mely a másik végen visszaverődvén az egyenesen jövő hullámsorral találkozik, s álló rezgéseket hoz létre; a húr ekkor részekre oszlik, melynek mindegyike egyenlő az említett hányszoros résszel, s rezgési csomók által választatnak el egymástól. A rezgési csomókat papírnyiretek által, vagy hosszú porhanyó kötélen láthatóvá tehetjük.”

(Subic Simon: Természettan, Pest, 1862.)

 
Ha a mikrohullámú sütő forgótányérját eltávolítjuk, és a sütőteret csokitáblákkal kibéleljük, majd a sütőt rövid ideig elindítjuk, azt tapasztaljuk, hogy a csokoládé meghatározott helyeken megolvad. A jelenség magyarázata, hogy a sütőben mikrohullámú elektromágneses állóhullám jött létre, s ennek duzzadó helyeinél megolvadt a csokoládé.   

Ismertesse, hogyan hozhatunk létre állóhullámokat egy rugalmas gumikötélen, melynek (csak) az egyik végét rögzítettük!

Milyen feltételek teljesülése esetén hoznak létre a kötélen terjedő haladó hullámok állóhullámot?

Készítsen ábrát, melyen bemutatja az állóhullám nevezetes pontjait és a hullámhosszát!

Hasonlítsa össze az állóhullámot az azt létrehozó haladó hullámmal!

Milyen fizikai mennyiségek azonosak a két esetben?

Írja le az állóhullám haladó hullámtól eltérő sajátságait, amplitúdó- és fázisviszonyait!

Ismertessen két további, a hétköznapi életben előforduló példát az állóhullámokra!

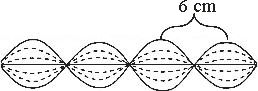
A sütő által létrehozott mikrohullám frekvenciája $2,45\ \mathrm{GHz}$, a csokoládétáblán a közvetlen szomszédos megolvadt részek távolsága $6\ \mathrm{cm}$. Becsülje meg ezeknek az adatoknak a segítségével a fény (mikrohullám) terjedési sebességét!

Miért érdemes forgótányért alkalmazni a mikrohullámú sütőkben?

A feladat eleje zavaros: 

"Ismertesse, hogyan hozhatunk létre állóhullámokat egy rugalmas gumikötélen, melynek (csak) az egyik végét rögzítettük!"

Egyrészt mit értünk az alatt, hogy csak az egyik vége van rögzítve?

• vagy azt, hogy a másikat rángatjuk (fel-le), ahogy azt a fizika órákon bemutatni szokás
• vagy azt, hogy a rugalmas kötés másik vége szabad (ezt magasból lelógatott gumiszállal lehetne bemutatni, bár ezt nemigen szokás)

Akármelyikre is gondoltak a feladat kitűzői, a javítási útmutató önellentmondásos, ugyanis a kötél hossza és a kialakuló állóhullám hullámhossza közötti összefüggésként megadott két képlet:

\[l=k\cdot \frac{\lambda}{2}\]

\[l=(2k+1)\cdot \frac{\lambda}{4}\]

közül az első a "mindkét vég rögzített" esetre vonatkozik, a második viszont az "egyik végén rögzített, a másik végén szabad" esetre.

Az állóhullám létrehozásának ismertetése:

1 pont

Például a kötél másik végét rezgésbe hozzuk, s megfelelő frekvenciájú rezgés esetén a kötélen kialakul az állóhullám.

Az állóhullám haladó hullámokból való keletkezésének ismertetése:

3 pont

Azonos hullámhosszú és frekvenciájú hullámok találkozásakor, általában visszaverődés révén jön létre állóhullám. Az állóhullám kialakulásának feltétele egy rugalmas kötélen, hogy a hullámhossz és a kötél hossza megfelelő arányban álljanak egymással.    
\[l=k\cdot \frac{\lambda}{2}\]

vagy

\[l=(2k+1)\cdot \frac{\lambda}{4}\]

A hullámhossz-duzzadóhely és -csomópont bemutatása ábrán:

3 pont

Az állóhullám haladó hullámmal azonos jellemzőinek bemutatása:

2 pont

Az állóhullámot keltő haladó hullámok frekvenciája és hullámhossza azonos az állóhulláméval.

Az eltérő sajátosságok bemutatása:

4 pont

Az állóhullám két szomszédos csomópontja között a hullámtér pontjai azonos fázisban, eltérő amplitúdóval rezegnek. Egy belső csomópont két oldalán ellentétes fázisú rezgés jön létre. A haladó hullámban a hullámtér pontjai folyamatosan változó fáziskülönbségű, azonos amplitúdójú rezgést végeznek.

További példák ismertetése állóhullámra:

2 pont

Hangszerek, membránok, rezonancia jelenségek stb.

A fény sebességének becslése:

2 pont

\[c=\lambda\cdot f\]

\[c=12\ \mathrm{cm}\cdot 2,45\ \mathrm{GHz}\]

\[c=294\ 000\ \mathrm{\displaystyle\frac{km}{s}}\]

  

A forgótányér alkalmazásának magyarázata:

1 pont

Az állóhullám duzzadóhelyein melegszik a legjobban az étel. A tányér forgása révén az étel mindig más része fordul a duzzadóhelyek „alá”.

Összesen: 18 pont