Az alábbi csigasor úgynevezett Arkhimédeszi csigasor. Az elrendezés lényege, hogy ilyen módon minden egyes mozgó csiga ismételten felezi a rajta lévő terhelést. A csigákkal egy \(\mathrm{12\ kg}\)-os testet szeretnénk megemelni.
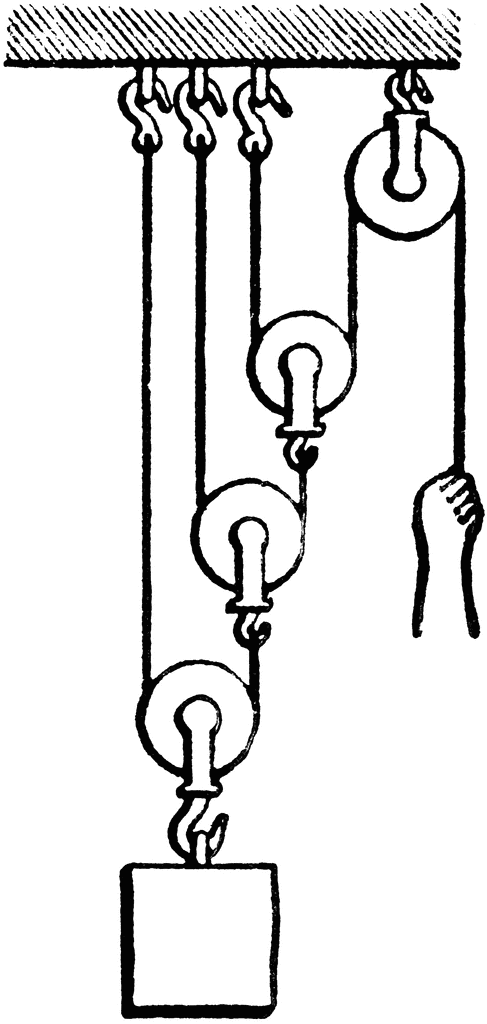
a) Mekkora erő szükséges ehhez, ha a csigák tömege elhanyagolható?
\(15\ \mathrm{N}\)
A bevezetőben leírtaknak megfelelően minden egyes csiga felezi a szükséges erőt, vagyis
\[F=\frac{m\cdot g}{2\cdot 2\cdot 2}\]
\[F=\frac{12\ \mathrm{kg}\cdot 10\ \mathrm{\displaystyle \frac{m}{\ s^2}}}{2\cdot 2\cdot 2}\]
\[F=\frac{120}{8}\]
\[F=15\ \mathrm{N}\]
b) Mekkora erő szükséges ehhez, ha a csigák tömege \(2\ \mathrm{kg}\)?
\(32,5\ \mathrm{N}\)
Az első csiga és a test tömege együtt
\[12\ \mathrm{kg+2\ kg=14\ kg}\]
ezért a második csigát
\[\frac{14\ \mathrm{kg}}{2}=7\ \mathrm{kg}\]
terheli.
Hozzávéve ehhez a második csiga tömegét, a harmadik csigán
\[\frac{7\ \mathrm{kg}+2\ \mathrm{kg}}{2}=\frac{9\ \mathrm{kg}}{2}=4,5\ \mathrm{kg}\]
terhelés jelenik meg.
Az utolsó csiga \(2\ \mathrm{kg}\)-ját is hozzáadva, akkor nekünk
\[F=\frac{(4,5\ \mathrm{kg}+2\ \mathrm{kg})\cdot g}{2}\]
\[F=\frac{6,5\cdot 10}{2}\]
\[F=32,5\ \mathrm{N}\]
erőt kell kifejtenünk.
Ugyancsak helyes gondolatmenet, hogy a teher megtartásához (súlytalan csigák esetén) szükséges, az a) kérdésben kiszámolt \(15\ \mathrm{N}\) erőn felül a három, egyenként
\[m\cdot g=2\ \mathrm{kg}\cdot 10\ \mathrm{\frac{m}{\ s^2}}=20\ \mathrm{N}\]
súlyú mozgócsigát rendre
\[\frac{20\ \mathrm{N}}{8}=2,5 \mathrm{N}\]
\[\frac{20\ \mathrm{N}}{4}=5 \mathrm{N}\]
\[\frac{20\ \mathrm{N}}{2}=10 \mathrm{N}\]
erőkkel tarthatjuk meg, ezeket mind összeadva ismét \(32,5\ \mathrm{N}\) jön ki.
c) Mekkora munkavégzéssel járnak a súlytalan csigás illetve a \(2\ \mathrm{kg}\)-os csigás esetek, ha a terhet \(5\ \mathrm{m}\) magasba emeljük?
\(W=600\ \mathrm{J}\)
Az egyszerű gépekkel nem spórolunk munkát, tehát
\[W=m\cdot g\cdot h\]
\[W=12\ \mathrm{kg}\cdot 10\ \mathrm{\frac{m}{\ s^2}}\cdot 5\ \mathrm{m}\]
\[W=600\ \mathrm{J}\]
d) Mekkora munkavégzéssel járna, ha a terhet \(5\ \mathrm{m}\) magasba emeljük, és a csigák mind \(2\ \mathrm{kg}\)-osak?
\(W=1300\ \mathrm{J}\)
Legegyszerűbb megoldás, ha a b) kérdésben már kiszámolt, általunk kifejtett \(F\) húzóerőre és a kezünk elmozdulására írjuk fel az
\[W=F\cdot s\]
munkát. Ekkor a kezünk \(s\) elmozdulása nem azonos a teher elmozdulásával, hiszen mivel az erő minden mozgócsigánál feleződik, ezért az elmozdulásminden mozgócsigánál duplázódik, így a három mozgócsiga miatt az elmozdulás:
\[s=5\ \mathrm{m}\cdot 2^3\]
\[s=5\ \mathrm{m}\cdot 8\]
\[s=40\ \mathrm{m}\]
lesz, amit a \(W=F\cdot s\) egyenletbe írva:
\[W=32,5\cdot 40\ \mathrm{m}\]
\[W=1300\ \mathrm{J}\]
Az is helyes gondolatmenet, hogy az első csigát, és a terhet \(5\ \mathrm{m}\), a második csigát \(10\ \mathrm{m}\), míg a harmadik csigát \(20\ \mathrm{m}\) magasba emeljük, és az ezekhez szükséges munkavégzéseket adjuk össze.