TARTALOM
I. A hőtan fejlődésének áttekintése
- A hőelmélet őskora. Spekulatív hőelméletek
- Az első tudományos hőelmélet: a hőanyagelmélet
- Rumford, a modern hőelmélet úttörője
- A mechanikai hőelmélet kezdetei. Az energia megmaradásának elve
- Az entrópiafogalom megszületése
II. Az entrópia és az entrópiatétel szerepe a hőelméletben
- Kiegyenlítődési folyamatok
- Az entrópia hőelméleti értelmezése
- A kiegyenlítődési folyamatok és az entrópia változása
- A Carnot‑féle körfolyamat. A II. fajú perpetuum mobile lehetetlensége
- Clausius az entrópiatételről
- Az egyensúly különböző típusai. Az önreguláció szerepe a hőelméletben
- A hőelmélet fötételei
III. Az entrópia statisztikus jelentése
- Az anyag molekuláris szerkezetének hőelmélet jelentősége
- A statisztikus hőelmélet alapproblémái
- Entrópia és állapotvalószínűség
- Hőelmélet és információelmélet
- Az "információ" mennyiségi jellemzésének lehetőségei
- Néhány érdekes probléma
- Statisztikus ingadozások
IV. Clausius "hőhalál"‑tételének kritikája
- A Clausius‑féle "hőhalál"-tétel
- A "hőhalál"‑tétel érvényesülésének feltételei
- A világegyetem térbeli kiterjedésének problémája
- A "hőhalál" az energia- és impulzustétel szempontjából
- Az entrópiatétel érvényességének korlátai a fenomenologikus elméletben
- A hőelmélet statisztikus jellegéből adódó szempontok
- Az anyagi világ végtelenségének egy újabb lehetősége. Összefoglaló következtetések
BEVEZETÉS
A fizikának sok olyan fogalma és alapvető megállapítása van, amelynek megismeréséhez mindennapi gyakorlati tevékenységünk is elvezet. Az ilyen fajta problémákról nyilvánvalóan könnyebb írni. Jelen könyvecske tárgya olyan fogalom és a fizikának néhány olyan megállapítása, mely nem közvetlenül támaszkodik a mindennapi tapasztalatokra. Ha tehát ezt a kérdéskört is közel akarjuk hozni az olvasóhoz, meg kell találnunk azokat az áttételeket, amelyek közvetítésével a mindennapi ismeretekből kiindulva biztonsággal jutunk a tudomány elvontabb területére. Tudjuk, hogy az ilyen kirándulások a tudomány világába - még a legjobb idegenvezetővel is - több-kevesebb nehézséggel, zökkenővel járnak és csak akkor vagyunk hajlandóak megtenni az utat, ha az érdekesnek ígérkezik. Úgy hisszük, ez utóbbi feltétel - már csak az entrópiafogalom kiterjedt és érdekes alkalmazási területei miatt is - bizonyosan fennáll.
Az entrópiafogalom és az ún. entrópiatétel, mellyel a későbbiekben megismerkedünk, a hőelméletben központi szerepet játszik. Ha emellett még azt is figyelembe vesszük, hogy ma már a hőtan messze túlnőtt eredeti szűk keretein, mindjárt világosabban látjuk problémánk jelentőségét. A hőtan az energiaátalakulások törvényszerűségeivel foglalkozó tudomány és mint ilyen az energiagazdálkodási problémák tudományos alapjául szolgál. Hogy az energiagazdálkodás kérdése a társadalmi fejlődés szempontjából mily alapvető jelentőségű, azt már nem is kell külön magyaráznunk. Energiagazdálkodása azonban nemcsak az emberi társadalomnak, hanem sajátos vonatkozásban a világegyetemnek is van. Bár a világmindenségben elfoglalt helyünk és sorsunk nem oly közvetlenül jelentkező probléma, mint az előbbi, világnézeti szempontból mégis nagy jelentősége van. Ily módon az entrópiatétel sok, világnézeti szempontból érdeklődésre számot tartó vonatkozást rejt magában. Gondoljunk például a világegyetem ún. "hőhalálát" kijelentő idealista következtetésre, melynek állítólagos alapját éppen az entrópiatétel szolgáltatja. Ezzel azonban még korántsem soroltunk fel minden olyan területet, ahol az entrópiafogalom szerepet játszik. Az utóbbi években a művelődésre vágyó nagyközönség is érdeklődéssel fordul az információelmélet és ezen belül a kibernetika eredményei felé. Nos, az entrópiának ebben a tudományban is alapvető szerepe van.
Tehát, akár az energiagazdálkodás tudományos alapjai, vagy az információelmélet fogalomalkotásai és megállapításai, akár világegyetembeli sorsunk világnézeti vonatkozású kérdései után érdeklődünk, érdemleges választ csupán az entrópiafogalom és az entrópiatétel ismerete alapján kaphatunk. Enélkül éppúgy nem tudunk tájékozódni a jelzett területeken, mint a társadalmunkba becsöppent olyan egyén, aki nem ismeri például a pénz fogalmát és funkcióit.
Fentiekből szükségszerűen következik a tárgyalandó kérdések megválasztása. Először meg kell ismerkednünk a hőelmélet alapvető megállapításaival. Didaktikai szempontok azt diktálják, hogy a történeti fejlődés sorrendjét és állomásait kövessük, ugyanis ily módon tudjuk biztosítani a mindennapi élet ismereteiből kiindulva az elvontabb területekre vezető legkönnyebben járható utat. Megfelelő hőtani ismeretek birtokában már könnyebben megérthetjük az entrópiafogalom jelentését és a természet törvényeiben játszott szerepét. Mivel a hőtani jelenségekben igen nagy szerepe van az anyag molekuláris szerkezetének, a molekulák sokaságán uralkodó valószínűségi törvényekkel, az entrópia mélyebb, valószínűségszámítási értelmezésével is megismerkedünk. Ezen keresztül jutunk el aztán az információelméleti entrópiafogalomhoz. Végül külön foglalkozunk az entrópiatétel világnézeti vonatkozásaival.
E könyv megírásával elsősorban a modern fizika világnézeti kérdései után érdeklődő szélesebb nagyközönség számára kívántunk összefoglaló tájékozódást nyújtani. A fizika és a természettudományok más területein dolgozó szakemberekre való tekintettel azonban néhány kérdésnél (így elsősorban az entrópiafogalom statisztikus értelmezésének ismertetése során) nem zárkóztunk el az alaposabb, nagyobb - bár elemi - matematikai apparátus felhasználásával járó tárgyalástól. Ez azonban ne aggassza a matematikai alkalmazásban járatlan vagy attól már elszokott olvasót: az alkalmazott matematikai apparátus sehol sem lépi túl a középiskolában tanultakat; másrészt e részeket feltűnően apró betűkkel szedtük:$\large{^\ast }$ gondolatmenetünk tökéletesen érthető lesz akkor is, ha valaki ezen apróbetűs részeket első olvasásra - vagy akár véglegesen is - mellőzi.
I. A HŐTAN FEJLŐDÉSÉNEK ÁTTEKINTÉSE
1. A hőelmélet őskora. Spekulatív hőelméletek
Őskori leletek azt bizonyítják, hogy már több százezer éve él ember a földön. A mi szempontunkból az az érdekes, hogy a leletek mellett rendszerint ott van az ún. "tűzpad", az ősember tűzhelye. (Ilyen tűzhelyet Magyarországon is találtak néhány évvel ezelőtt a Bükk‑hegységben, a Szilvásvárad melletti Istállóskő nevű barlangban.) E leletek alapján egyértelműen megállapítható, hogy a tűz ismerete és felhasználása több százezer éves múltra tekinthet vissza. Nyilvánvaló, hogy kezdetben az ember még nem értett gerjesztéséhez, csupán a természetben már meglevő tüzet tudta tovább fenntartani és céljainak megfelelően felhasználni. Hogyan keletkezett az ember által használt első láng, nem tudjuk pontosan. Valószínűleg villámcsapás, vagy más természeti jelenség (tűzhányó, földgáz meggyulladása stb.) idézhette elő. A tűz valóban félelmetes természeti jelenség, így nem csodálkozhatunk azon, hogy a primitív ember isteni eredetűnek tartotta, s a jelenleg is élő primitív népek vallásában szintén igen nagy szerepet játszik.
Az emberi társadalom fejlődésével a tűznek egyre nagyobb szerepe lett a mindennapi életben. Így egyre fontosabbá vált, hogy az ember saját maga is tudjon tüzet gerjeszteni. E probléma megoldásához is a tapasztalás nyújtott segítséget. Felismerték, hogy a dörzsölés mindig az összedörzsölt tárgyak felmelegedésével jár, azaz rájöttek arra, hogy a mozgás, amennyiben súrlódással lefékezik, hővé alakítható át. Igen nagyjelentőségű volt ez a felismerés, amely szintén még a történelem előtti időkből származik. Engels szerint "A mechanikai mozgás hővé alakításának gyakorlati felfedezése olyan ősrégi, hogy ettől lehetne számítani az emberiség történetének kezdetét. Bármilyen felfedezések is előzhették meg a szerszámok és az állatszelidítés terén, a dörzsöléssel nyert tűz volt az a találmány, amellyel az emberek első ízben kényszerítettek szolgálatukba egy élettelen természeti erőt. S hogy ennek az óríási haladásnak szinte mérhetetlen hordereje mennyire bevésődött érzésvilágunkba, mutatja még a mai népi babona is. (...) Jóval azután, hogy a tűzgyújtás más módjait ismerték, a legtöbb népnél minden szent tüzet dörzsöléssel kellett létrehozni. De a legtöbb európai országban mind a mai napig él még az a népi babona, hogy csodatevő erejű tüzet (...) csak dörzsöléssel szabad gyújtani. Úgyhogy a hálás emlékezés az embernek a természeten aratott első nagy győzelmére egészen napjainkig tovább él még - bár félig öntudatlanul - a népi babonában, a világ legműveltebb népei pogány‑mitológiai emlékeinek maradványaiban."$^1$
Sokezer év óta ismerte már az ember a mozgás hővé való átalakításának lehetőségét, de a folyamat megfordítását nem tudta (sőt hozzátehetjük, hogy nem is nagyon igyekezett) megvalósítani. Pedig a józan ész is azt diktálja; hogy nemcsak a mozgás alakítható hővé, hanem a hő is visszaalakítható mozgássá. Kb. kétezer éve ismeretes a fordított folyamat is. Hérón szerkesztette az első "gépet", mely hőnek mozgássá való átalakítására alkalmas: számos, a hő mozgatóerejét felhasználó eszközt készített, ezek az eszközök azonban nem voltak egyebek játéknál, gyakorlati célokra nem használták fel őket és tudományos jelentőségüket nem ismerték fel. Az a tény, hogy a hő mozgássá alakítható, két szempontból is igen fontos. Egyrészt gyakorlatilag hasznosítható, másrészt közelebb visz annak a kérdésnek megoldásához is, hogy mi a hő. A két kérdés szorosan összefügg egymással. A hő természetének ismerete megkönnyíti a gyakorlati alkalmazást, a gyakorlati alkalmazások viszont elősegítik az elmélet fejlődését. Azt szokták mondani, hogy Hérón találmánya megelőzte saját korát. Ez azt jelenti, hogy abban az időben a hő mozgatóerejének felhasználása nem volt társadalmi szükséglet és, ha felismerték is, csupán érdekesség maradt; nem vált gyakorlattá, nem hatott ösztönzőleg a tudományos elméletek továbbfejlesztésére. Csak a kapitalizmus kialakulásakor kezd problémává válni az energia megszerzése. Az első kapitalista üzemek energiaszükségletét emberi munkával már nehéz, vagy egyáltalán nem lehet fedezni. Ez a tény a XVIII. században kezdi hatását éreztetni és csak ekkor kezdenek tudatosan rátérni arra az útra, amely a gőzgép feltalálásához vezetett.
Az ókort és a középkort nem foglalkoztatta az energiagazdálkodás problémája. Amire szükségük volt az akkori kizsákmányoló osztályoknak, azt bőségesen megkapták a rabszolgák és jobbágyok tömegei által szolgáltatott emberi munkavégző képességben. Igaz, hogy egyéb vonatkozásban bizonyos hőjelenségeket gyakorlatilag egyre nagyobb mértékben használtak fel, azonban az ehhez szükséges ismeretek nem nagyobbak annál, amennyit minden józanul gondolkodó és szemlélődő ember maga megfigyelhet. Mire használják ebben az időben a hőt? Az ókorban már fejlett volt a kohászat, ennek tudományos alapja pedig az a már akkor is közismert tény, hogy a hő hatására a testek halmazállapota megváltozik és hő hatására vegyi átalakulások jönnek létre. Ismerték és felhasználták a testek hőokozta tágulásának jelenségét, valamint a fagyást, olvadást, forrást. Ezt a kort tehát az jellemzi, hogy a közismert hőjelenségek bőségesen elegendőek a termelés igényeinek kielégítésére. A gyakorlat nem vet fel problémákat s ezek rendszerint csupán a spekulatív okoskodásban merülnek fel; így viszont nincs sok közük a valósághoz. Másrészt hozzátehetjük, hogy a középkorban az Egyház tekintélye amúgy sem segítette elő, sőt rendszerint gátolta az egzakt természettudományok kifejlődését és haladását. Nyilvánvaló, hogy a valóságtól elszakadt elmélet nem válhatik tudománnyá, nem fejlődhetik. Az a különleges helyzet állt elő ilyenformán, hogy a józanul gondolkodó és szemlélődő embernek sokkal alaposabbak voltak a hőre vonatkozó ismeretei, mint a tudósoknak. Különös helyzet, de mégsem csodálkozhatunk rajta, ha meggondoljuk, hogy a hétköznapi embernek ezekben a kérdésekben sokkal szorosabb volt a kapcsolata a gyakorlattal, mint a tudósoknak. A fizika története bőséges illusztrációval szolgál az itt elmondottakhoz.
2. Az első tudományos hőelmélet: a hőanyagelmélet
Az ó- és középkor természetről alkotott felfogásában döntő szerepet játszott az ún. négy elem tana. Eszerint a világ négy elemből, négyféle alkotórészből áll: levegőből, vízből, földből és tűzből. A hőjelenségeket is a négy elem egymásrahatásából igyekeztek megmagyarázni. Ez a felfogás egyáltalán nem törődött a hétköznapi megfigyelés által megállapított törvényszerűségekkel, magyarázatai rendkívül bonyolultak és gyakorlatilag használhatatlanok voltak.
A négy elem tanán felépülő elmélet egy darabig, bár hasznot sem hajtott, különösebb kárt sem okozott a tudomány fejlődésében. Később azonban egyre inkább kiütköztek hiányosságai: erősen gátolta a hőelmélet tudományos megalapozását. Az újkor elején fellendülő ipar és a gyakorlati élet minden vonatkozásban komolyabb igényeket kezdett támasztani a hőelmélettel szemben. Szükségessé vált a hőmérséklet mérése, továbbá azoknak a mennyiségi törvényeknek a pontos feltárása, amelyek a hő okozta állapotváltozásokra vonatkoznak. Ki kell emelni pl. azt a kérdést, hogy a különböző anyagok milyen eltéréseket mutatnak, ha ugyanakkora hőhatásnak teszik ki őket. Közismert tény, hogy különböző anyagok ugyanakkora hőhatásra különbözőkép melegszenek fel. Pl. ha $1\ \mathrm{liter}$ $(1\ \mathrm{kg)}$ $20\ \mathrm{{}^\circ Celsius}$ hőmérsékletű vízbe $80\ \mathrm{{}^\circ Celsius}$ hőmérsékletű $1\ \mathrm{kg}$‑nyi alumíniumot, ill. ugyanilyen hőmérsékletű és tömegű ezüstöt teszünk, a víz melegedni kezd, ugyanakkor a benne levő alumínium ill. ezüst lehűl. Elérnek egy közös hőmérsékletet, amely $20\ \mathrm{{}^\circ Celsius}$ és $80\ \mathrm{^\circ Celsius}$ között van. Alumínium esetében a közös hőmérséklet nagyobb: kb. $30\ \mathrm{{}^\circ Celsius}$, ezüst esetében már csak kb. $23\ \mathrm{{}^\circ Celsius}$, tehát jóval kevesebb. Ezt a tulajdonságot a köznapi nyelv úgy fejezi ki, hogy az alumínium jobban tárolja a meleget, mint az ezüst. Tudományos nyelven azt mondjuk: az alumínium fajhője (hőkapacitása, hőbefogadóképessége) nagyobb, mint az ezüsté. Az itt közölt tapasztalatok elemzése alapján a továbbiakban már könnyen eljuthatunk a hőanyagelmélet lényegének és jelentőségének megértéséhez.
A hőmérő felfedezése is jelentősen hozzájárult a további fejlődéshez. Az első hőmérőt Galilei szerkesztette (1590 táján), amely ugyan még sok szempontból tökéletlen volt, de alapjául szolgált a további fejlődésnek. A hőmérőre ekkor már igen nagy szüksége volt a társadalomnak. Santorio professzor (1561‑1636) már az orvosi gyakorlatban is használja. Továbbá, mivel az anyagok ipari megmunkálásában a hőnek már előzőleg is igen fontos szerepe volt, a nagyobb igények nagyobb pontosságot követeltek ezen a téren is. Most már nem volt megfelelő az ember sokszor megtévesztő, szubjektív hőbecslése, a hőmérséklet pontosabb mérésére volt szükség. Megemlítjük azonban, hogy még az 1800‑as évek elején, tehát jóval az első hőmérő megjelenése után sem volt tisztázva a hőmérséklet és a hőmennyiség fogalma közti különbség. "Meleg"‑ről beszéltek, amely mindkét fogalmat magában foglalta. (A hétköznapi életben gyakran ma sem tesznek különbséget közöttük.) Az itt fennálló elméleti zavar tisztázása kétségkívül a hőanyagelmélet érdeme: látni fogjuk, hogy ez az elmélet világosan megmagyarázza e két fogalom közti különbséget.
A hőanyagelmélet volt az első, amely tudományosan rendszerezte a hő természetére vonatkozó ismereteket és a jelenségek közti összefüggésekre is igyekezett rámutatni. Ebben az elméletben nincsenek üres és fölösleges spekulációk: a mindennapi tapasztalatra támaszkodik. Később látni fogjuk, hogy a "mindennapi tapasztalat" naivitása okozza egyúttal az elmélet egyik fő hiányosságát is: túlságosan ragaszkodik a hétköznapi szemlélethez, nem veszi kellő kísérleti kritika alá elgondolásait.
Mit mond ki a hőanyagelmélet? Azt állítja, hogy a közönséges, kézzelfogható és tapintható anyagon kívül van egy ún. hőanyag is, amely a közönséges anyaggal szemben, súlytalan. E felfogás szerint a hőanyag minden anyagi testben eleve benne van, továbbá: minél több hőanyag van egy testben, annál nagyobb a hőmérséklete. Ha két különböző hőmérsékletű test érintkezik egymással, akkor a hőanyag a nagyobb hőmérsékletű testből a kisebb hőmérsékletű testbe áramlik át. Ennek következtében a hőanyagot veszítő test hőmérséklete csökken, a hőanyagot felvevő test hőmérséklete nő. A folyamat addig tart, amíg a két test közös hőmérsékletű nem lesz. A dolog megértését nagymértékben megkönnyíti a közlekedőedényekkel való összehasonlítás. A tapasztalat azt mutatja, hogy az egymással kapcsolatban levő edények mindegyikében ugyanolyan magasságú a folyadékoszlop. Ha valamelyik edénybe vizet öntünk, ettől még nem lesz ebben az edényben magasabb folyadékszint: a beöntött víz egy része átfolyik a többi edénybe és az egyensúly csak akkor áll be, ha mindegyikben ugyanazon szinten áll a folyadék. Tehát, ha két vízzel telt edény kapcsolatban van egymással, a szintkülönbség kiegyenlítődni igyekszik, és a folyamat mindaddig tart, míg a vízállás egyenlő szintre nem jut mindkét edényben. Láttuk, hogy hasonló a helyzet a különböző hőmérsékletű testeknél is. A hőanyag megfelelője közlekedőedényeknél a folyadék, a hőmérséklet megfelelője a folyadékoszlop magassága. A hasonlóság még ezen túlmenőleg is fennáll. Adott folyadékmennyiség mellett a közös szintmagasság az edények alapterületétől ill. keresztmetszetétől is függ. Ha nagy az alapterület, ugyanaz a folyadékmennyiség nyilvánvalóan alacsonyabb szintemelkedést fog eredményezni, mint kis edénykeresztmetszet esetén. A közlekedőedények esetében a keresztmetszettel arányos térfogat (vagy másképpen befogadóképesség) megfelelője megtalálható a testek hővel szembeni viselkedésénél is. Egyik test több hőanyagot képes felvenni mint a másik, ahhoz, hogy a hőanyag mindkét testben ugyanazt a hőmérsékleti szintet érje el. Igy pl. az alumíniumnak kereken négyszer akkora a hőbefogadóképessége, mint az ezüstnek. Az előbbiek szerint ez azt jelenti, hogy a hőanyag szempontjából ugyanolyan tömegű alumínium és ezüst közül az alumínium négyszer akkora térfogatú edénynek számít, mint az ezüst. A víz hőbefogadóképessége pedig az alumíniuménak is ötszöröse, tehát az ezüstének húszszorosa.
Mivel a közlekedőedények folyadékszintjének és a különböző hőmérsékletű testek hőmérsékletének kiegyenlítődése hasonló módon megy végbe, a kétféle folyamat hasonló felépítésű törvényszerűségnek engedelmeskedik. Ennek bemutatására tekintsünk két egymással összeköttetésben álló, de pillanatnyilag még csappal elválasztott henger alakú edényt, melyek alapterülete $a_1$ és $a_2$, a bennük levő folyadék szintjének magassága pedig $h_1$ és $h_2$. A két edényben levő folyadékmennyiség össztérfogata nyilván:
$$V=a_1h_1+a_2h_2$$
A csap megnyitása és a kiegyenlítődés után a folyadékszint közös lesz, tehát a térfogat:
$$V'=a_1h+a_2h$$
ahol $h$ a közös szintmagasság. Mivel a kiegyenlítődés folyamata közben a folyadék mennyisége, s így a térfogata sem változik meg, $V=V'$ azaz
$$a_1h_1+a_2h_2=(a_1+a_2)h$$
tehát
$$h=\frac{a_1h_1+a_2h_2}{a_1+a_2}$$
Ugyanilyen alakú formula adja meg a hőmérsékletkiegyenlítődés után beálló közös hőmérsékletet. Ekkor $h_1$, $h_2$ és $h$ hőmérsékleti értékek, $a_1$ és $a_2$ pedig hőkapacitások.
Fenti kép vezette Richmann szentpétervári fizikust a XVIII. században a következő kalorimetriai probléma megoldására: Milyen közös hőmérsékletet vesz fel az eredetileg $m_1$ és $m_2$ tömegű, valamint $t_1$ és $t_2$ hőmérsékletű két vízmennyiség keveréke? Nyilvánvaló, hogy a közös hőmérséklet:
$$t=\frac{m_1t_1+m_2t_2}{m_1+m_2}$$
ugyanis a keveredő komponensek azonos anyagúak lévén, hőkapacitásuk tömegükkel arányos.
A hőanyagelmélet tudatos kifejtése a XVIII. század második felére esik. A "hőkapacitás" és "fajhő" elnevezések ebből a korból származnak. Érdekes, hogy a "hőmérséklet" és "hőmennyiség" fogalma csak a XVIII. század legvégén különböztetődik meg élesen egymástól. Érthető, hogy az elmélet tudatos kifejtése egyúttal a bukás kezdetét is jelenti. Ugyanis az ellentmondások ekkor mutatkoznak meg legvilágosabban. így pl. a "rejtett" (latens) hő fogalma teljesen érthetetlen a hőanyagelmélet szempontjából. "Latens hő"-nek hívjuk azt a hőmennyiséget, amely nem idéz elő hőmérsékletváltozást. Például az olvadó jég lehűti ugyan a vele érintkező testet, de hőmérséklete csak akkor kezd emelkedni midőn olvadása már befejeződött. Tehát az egyik test lehűl, hőanyagot ad le, ezt a jég felveszi, de nem hőmérséklete emelésére, hanem valamiképp saját halmazállapotának megváltoztatására fordítja.
Kezdetben azonban a negatívumoknak kisebb fontosságot tulajdonítottak, abban a reményben, hogy az elmélet megfelelő módosításával ezek kiküszöbölhetők lesznek. Lavoisier pl., aki a flogisztonelméletet$^2$ megdöntötte, a hőanyagelmélettől nem tudott elszakadni.
Az a körülmény, hogy a különböző hőmérsékletű testek hőmérsékletkülönbsége kiegyenlítődni igyekszik, és a kiegyenlítődés a közlekedőedénybeli szintkiegyenlítődéshez hasonló módon történik, kezdetben a hőanyagelmélet jogosságát látszott igazolni. Az elmélet alapján végzett számítások, mint láttuk, megerősítik ezt a felfogást. Mai szemmel nézve azt mondhatjuk, hogy a hőanyagelméletben van valami igazság, de mégsem egészen helyes, mert sok jelenséget nem tud a valóságnak megfelelően megmagyarázni. Hogy a hőanyagelmélet mennyire beleevődött még a mai fejlettebb tudományos felfogásba is, tudományos nyelvünk is bizonyítja. Azt mondjuk, hogy a "meleg" a nagyobb hőmérsékletű hely felől a hidegebb felé "áramlik". A "meleg" szó itt végeredményben hőanyagot jelent, amit az "áramlás" kifejezés is bizonyít. A hőkapacitás (hőbefogadóképesség) szintén szerepel a mai tudományos elméletben, holott a szó eredete és szó szerinti jelentése szintén a hőanyagfelfogásra utal. Ha a tudományban nem okoz zavart ez a szóhasználat, mi is nyugodtan használhatjuk. A köznapi nyelvben egyébként, más vonatkozásban is, sok szó és szóösszetétel szerepel, amelyek valamilyen régi, a közvetlen szemléleten és a "józan ész" felfogásán alapuló elmélet maradványai. Pl. napkeltéről és napnyugtáról beszélünk, holott tudjuk, hogy nem a Nap kel fel, illetőleg nyugszik le, hanem a Föld fordul el a Naphoz képest.
A hőanyagelméletnek utolsó nagy eredménye a hővezetésnek Fourier‑től származó elmélete. Fourier idevágó munkája már a XIX. század elejére esik és bár ekkor már nyomós ellenérvek voltak ismeretesek a hőanyagelmélettel szemben, munkájában ezeket figyelmen kívül hagyja. (Fourier a hőmennyiséget szubsztanciális valóságnak tartja.)
Egyébként ebben az időben már csak igen mesterkélt magyarázatok árán tudják a hőanyagelméletet menteni, de legtöbben mégis kitartanak mellette. Maga Carnot is, aki egyébként a modern hőelmélet egyik előfutára volt, szintén a hőanyagelmélet alapján állt. Nézete szerint a hőnek munkanyerésre való felhasználása hasonló folyamat eredménye, mint a vízesések energiájának kihasználása. Ahogyan a víznek magasabb szintről alacsonyabb szintre való esése során munkát nyerünk, ugyanúgy a hőanyag magasabb hőmérsékleti szintről alacsonyabb hőmérsékleti szintre való jutásából származik a nyert munka.
Valóban, igen csábító és - meglepően - igen gyümölcsöző a hasonlat, segítségével pl. ki tudjuk számítani az ideálisan működő gőzgép hatásfokát. A vízesés azáltal szolgáltat munkavégzésre felhasználható mozgási energiát, hogy bizonyos időszakaszonként $m$ tömegű víz $h_1$ magasságból $h_2$ magasságú szintre esik le. Az eredeti helyzeti energia tehát ($g$‑vel jelölve a gravitációs gyorsulást):
$$mgh_1$$
a maradék helyzeti energia pedig
$$mgh_2$$
Munkára a kettő különbsége használódik fel:
$$mgh_1-mgh_2=mg(h_1-h_2)$$
aminek az eredeti energiához való viszonya (ezt hatásfoknak is nevezhetjük):
$$\frac{mg(h_1-h_2)}{mgh_1}=\frac{h_1-h_2}{h_1}$$
Víz helyett most már a hőanyagnak $T_1$ hőmérsékletű "szint"‑ről $T_2$ hőmérsékletű "szint"‑re való esését vizsgálva a fentiek analógiájára a hőnek
$$Q_1=cT_1$$
kezdeti és
$$Q_2=cT_2$$
végállapotbeli energiát kell tulajdonítanunk ($c$ a hőkapacitás). Munkavégzésre a kettő különbsége használható fel
$$W=cT_1-cT_2$$
aminek a felvett energiához való viszonya
$$\frac{W}{\ Q_1}=\frac{c(T_1-T_2)}{CT_1}=\frac{T_1-T_2}{T_1}$$
Rendkívül érdekes, hogy az indoklás naiv volta ellenére az eredmény teljesen helytálló, amiről a továbbiakban meg is fogunk győződni.
Carnot szóhasználata világosan elárulja, hogy szerzője a hőanyagelmélet alapján áll. A tűz (feu), a hő (chaleur), a hőmennyiség (calorique) fogalmát élesen megkülönbözteti egymástól és a "tűz mozgató erejé"‑ről (Puissance motorice de feu) beszél. Carnot szerint a mozgató erő kifejtése közben a hőanyag - mint imponderabilium - mennyisége változatlan marad. (Miként a vízesésben lezúduló víz mennyisége sem változik meg a munkavégzés következtében.)
Carnot e tévedését Clapeyron még 1843‑ban is fenntartja. Tudvalevőleg Clapeyron eredményei nagyrészt nem egyebek, mint Carnot megállapításainak matematikai formában történt megfogalmazásai. Carnot maga semmilyen matemetikai apparátust nem használt és tételeit sem matematikai formában fogalmazta meg.
3. Rumford, a modern hőelmélet úttörője
Nyilvánvaló, hogy az elméleti elgondolások egymással és a tapasztalással való helyes és eredményes összeegyeztetését olyan tudós indíthatta el, akinek a tőkével szoros kapcsolatai voltak és aki már ezért is mentes volt a különböző előítéletektől. Ez a tudós Rumford volt, aki logikusan átgondolt kísérletsorozataival a legdöntőbb csapásokat mérte a hőanyagelméletre. Az új elmélet rendszerét ugyan ő sem tudta megalkotni, de a hiányosságokra világosan rámutatott. Ezek ismeretére pedig feltétlenül szükség volt a további fejlődéshez. Rumfordot kutatásaiban nem a "tiszta tudományos igazság" iránti rajongás vezette. Nagyon is gyakorlati ember volt. Élete nem egyéb: egyetlen nagy üzleti vállalkozás szolgálata.
Rumford - eredeti családi nevén Thompson - 1753-ban született az Amerikai Egyesült Államokban. Szülei gazdag angol gyarmatosok voltak. Apját korán elvesztette, anyja pedig nem törődött vele, úgyhogy idegenek nevelték fel. A családi kör meghitt melegének hiányáért egyetlen "kárpótlása" a nagyapjától örökölt vagyon volt. Nevelőszülei ugyanis az örökségből kitűnő nevelésben részesítették a jóeszű gyermeket. Tíz éves korától csillagászatot és matematikát tanult a falubeli paptól. Alig tizenhárom éves korában megvált otthonától és kereskedősegédnek szegődött egy Salem nevű városkába. De közben ott is szakadatlanul tanult. Tudatában volt képességeinek és erős becsvágy fűtötte. A tudománnyal is azért foglalkozott, hogy könnyebben boldoguljon az életben. Tizenhat éves korára olyan képzettségre tett szert, hogy otthagyta a kereskedelmi pályát és visszament szülőfalujába, ahol magániskolát nyitott. És közben tanult, tanult és mindent megfigyelt, amit érdekesnek és hasznosnak tartott. Későbbi visszaemlékezéseiben erről az időszakról ezt írta: "... a környezetemben előforduló jelenségeket, ha a hővel és hatásaival csak a legtávolabbi összefüggésben voltak is, a legnagyobb gonddal vizsgáltam meg. Ennek köszönhetem azoknak a kísérleteknek eszméit, amelyeket e tárgyra vonatkozóan végeztem".
Rumford további életpályája igen kalandos volt. Először belépett az amerikai hadseregbe. Később az angol hadseregbe ment át, azután Németországba került és rövidesen bajor hadügyminiszter lett. Ebben a minőségben hatalmas hadiüzemeket létesített a hadsereg számára. Állami megbízásból azzal is foglalkozott, hogyan lehet nagy tömegek számára a leggazdaságosabban főzni, fűteni, világítani. Mindezen gyakorlati munkák kiválóan alkalmasak voltak tudományos elgondolásainak kidolgozására és továbbfejlesztésére. Említettük már, hogy ebben az időben egyre többen akadtak olyan tudósok, akik a mechanikai hőelmélet (l. később) kezdetleges formájának hívei voltak. Rumford ezek nyomdokain haladt és a hőanyagelmélet tarthatatlanságának kimutatását tűzte ki főcéljául.
Rumford elgondolása az volt, hogy amennyiben csakugyan van hőanyag, úgy az a környezetétől elszigetelt testből csak korlátolt mennyiségben vonható ki. Ismeretes, hogy az ágyú elsütésekor visszalökődik. A visszalökés annál nagyobb, minél nagyobb sebességgel hagyja el az ágyúgolyó a löveget. Rumford mérési eljárást igyekezett kidolgozni a visszalökés nagyságából a kilőtt golyó sebességének meghatározására. Itt arra az érdekes tapasztalatra, jutott, hogy a csupán puskaporral töltött ágyú a lövés következtében sokkal jobban felmelegszik, mint amikor golyó is van a csőben; ha több lövedéket töltött be, a felmelegedés még kisebb lett. Ez a kísérlet tehát azt mutatja, hogy az ágyúgolyó mozgása felemészti a puskapor robbanása által keletkező hőt, a hő mozgássá alakul és a hőanyag, ha volna ilyen, az említett esetben elveszne.
Másik fontos észlelését az ágyúcsövek fúrásával kapcsolatban tette (1798). Feltűnt neki, hogy fúrás közben milyen erősen felmelegszik a cső, és a keletkező fémforgács. Honnan származhatik az itt keletkező meleg? Ha van hőanyag és az okozza a melegséget, akkor itt csakis valamilyen rejtett hő felszabadulásáról lehet szó, azonban sem a cső, sem a fémforgács, sem a fúrógép, sem pedig a környező levegő nem mutatott semmilyen elváltozást. Fajhője sem változott egyiknek sem. (A fajhő kisebbedése nyilván hőmérsékletemelkedéssel jár. A közlekedőedényekkel való analógia szerint a kisebb alapterületű edényben, mely kisebb hőbefogadóképességű anyagnak felel meg, ugyanaz a folyadékmennyiség magasabb szintet ér el.) Végül azt is tapasztalta, hogy az állítólagos rejtett hőanyagkészlet sohasem apad ki, dörzsöléssel korlátlan mennyiségben tud hőt termelni, anélkül, hogy az összedörzsölt anyagok bármilyen szerkezeti elváltozást is mutatnának. Ha a meleg valóban a hőanyagtól származna, a hőanyagnak egyszer el kellene fogynia az összedörzsölt tárgyakból, ilyen fogyásnak azonban nyomát sem találta. Rumford ilyen módon arra az eredményre jutott, hogy a hőállapotot nem valamilyen hőanyag, hanem az anyag belső mozgása idézi elő. Dörzsölésnél azért nő a hőmérséklet, mert az összedörzsölt tárgyak látható mozgási energiája állandóan átalakul a testek belső (molekuláris) mozgási energiájává.
Az eredmények és a levont következtetések nagy feltűnést keltettek és mások is igyekeztek hasonló temészetű ellenőrző kísérleteket végezni. Davy, a híres kémikus, két összedörzsölt jégdarabon végzett méréseket és megfigyelései teljes mértékben igazolták Rumfordot. Sokan mégis ragaszkodtak a hőanyagelmélethez és iparkodtak Rumford és Davy kísérleteit (1839) a hőanyagelmélet alapján magyarázni. Vállalkozásuk azonban nem járhatott sikerrel, s a hőanyagelmélet lassan‑lassan hitelét veszítette.
4. A mechanikai hőelmélet kezdetei. Az energia megmaradásának elve
Az új elmélet nem váratlanul jelent meg. A hőanyagelmélet még javában tartotta magát, sőt még ki sem alakult, amikor egy‑egy kutató már a további fejlődés alapjait kezdte lerakni. Azonban ahogyan Hérón találmányai a meleg mozgató erejére vonatkozólag korukat meghaladó találmányok voltak, ezek az új elgondolások is meghaladták saját korukat. Erre az esetre megint csak az áll, hogy egyrészt a fejletlen kísérleti technika nem tette lehetővé az elmélet pontos mennyiségi ellenőrzését, másrészt: a társadalmi igények sem voltak még meg az ilyen haladottabb elméletekre. Fordítva: a fejletlen elmélet akadályozta a gyakorlati problémák helyes megoldását.
Az elmélet továbbfejlődésének tapasztalati alapja most az a már ismert jelenség volt, hogy a mechanikai mozgás hővé és fordítva, a hő mechanikai mozgássá alakítható. A hőanyagelmélet ezeket a tényeket nem vette mélyebb vizsgálat alá. Az 1700‑as évekkel azonban eljött az ideje azon jelenségek gyakorlati vizsgálatának is, amelyek a hő és a mozgás kapcsolatának elméleti jelentőségére is ráirányították a figyelmet.
Ez idők legnevezetesebb felfedezésének a gőzgép feltalálását kell tekintenünk. Nemcsak azért, mert ez egyúttal a "gépesítés" fejlődésének kezdetét is jelentette, hanem azért is, mert az elmélet továbbfejlődése szempontjából igen lényeges volt, hogy a hő is átalakítható mechanikai mozgássá. A gőzgép feltalálása természetesen nem egyetlen kutató munkájának eredménye. Fokozatosan jutottak el a gyakorlati alkalmazásáig.
Huyghens pl. olyan gépet tervezett, amelynél a mozgató‑erőt puskapor robbantásával akarta előidézni. Elgondolása szerint a puskapor‑gázok hengerben járó dugattyút mozgattak volna. Papin ezt úgy módosította, hogy puskapor helyett vízgőzt használt. A gőzgépnek ez a formája még igen tökéletlen volt. Polzunov orosz és később Watt angol kutató végezték el azokat a módosításokat, amelyekkel lényegében eljutottak a gőzgép mai formájához. Bár Polzunov előbb tette felfedezését, a tudományos világ az utóbbi időkig Wattot tartotta a gőzgép felfedezőjének. Ennek oka jórészt az, hogy Watt egy élelmes kereskedőben komoly pártfogóra talált. A gépet pénzverő, bányavíz szivattyú, majd gőzmalom hajtására használták fel. Az ipari felhasználás újabb lehetőségei vetődvén fel, Watt anyagi segítséget kapott kutatásainak folytatására, találmányának tökéletesítésére.
Az új technikai eredmények, kísérleti felfedezések és az új elméleti elgondolások a hő és a mozgás viszonyáról látszólag csak zűrzavart okoztak az elmélet fejlődésében. Két felfogás ütközött össze. Egyiknek erőssége a hagyomány volt, a másiké a jövő fejlődésébe vetett bizalom. Nagyon nehezen születtek meg azok a bizonyítékok, amelyek alapján már el lehetett dönteni, hogy a jövő fejlődés útja a hő és a mozgás kapcsolatának feltárásában áll. A továbbiakban ezt az elméletet mechanikai hőelméletnek fogjuk nevezni, mivel elgondolása szerint a hőjelenségeket az anyag atomjainak (molekuláinak) mechanikai mozgása idézi elő.
A hőjelenségeknek a mozgással való kapcsolatát különböző elméletekben többféle formában felvetették, mielőtt a mai molekuláris hőelmélet kialakult. Ezek az elméletek mintegy átmenetet képeznek a hőanyagelmélet és a mechanikai hőelmélet közt. Gassendi (1592‑1655) szerint a hőanyag atomos szerkezetű és a hőjelenségeket nem a hőatomok puszta jelenléte, hanem azok mozgása idézi elő. Kant szerint a hő nem egyéb éterrezgésnél. A francia forradalom idejéből ismert Marat Gassendiéhez hasonló nézetet vallott: a tűz atomos szerkezetű, az atomok mozgása kelti a tűz- és hőjelenségeket. Különleges érdemnek tekintsük‑e azokat az elgondolásokat, amelyek a mai molekuláris hőelmélettel mutatnak rokonságot? Nyilván indokolatlan volna, hiszen ezek éppen olyan spekulatív elméletek voltak, mint az előbb említettek. Kétségtelen előnye és érdeme azonban valamennyinek, hogy a hő és a mozgás egymásba való átalakulását egy általánosabb és a jelenségek bizonyos területén már kísérletileg igazolt törvény: a mozgás elpusztíthatatlanságának törvénye alá vonták.
A mechanikai hőelmélet egyik megalapozójának Rumfordot kell tekintenünk, akinek munkásságával már előbb foglalkoztunk. Ugyanis ő volt az, aki céltudatosan végrehajtott kísérleteivel tudományosan megmutatta a hőanyagelmélet tarthatatlan voltát. Az ő rendszerében már a hő és mozgás kapcsolatba állítása nem puszta spekuláció, hanem a kísérleti eredményekből tényszerűen folyó következmény.
Nagy előrehaladást jelentett továbbá annak a kérdésnek a megvizsgálása, hogy a hő mozgatóereje véges‑e vagy végtelen, és ha véges, akkor mekkora. Ezzel a kérdéssel Carnot (1824) foglalkozott és megállapította, hogy valahányszor a hő melegebb helyről hidegebbre áramlik, mindig munkát végez. Azt is megállapította, hogy az átfolyó hő, a nyert mechanikai munka, valamint a hőmérsékletesés egymással egyértelmű kapcsolatban állnak, azonban a kapcsolatot kvantitatíve nem tudta általánosan leírni. Carnot közel járt a hőelmélet második főtételének felfedezéséhez, de ebben megakadályozta őt, hogy akkor még az első főtétel sem volt ismeretes. Enélkül (ti. az energia‑tétel nélkül) pedig a második főtételt nem lehetett világosan felismerni.
Carnot ezeket az eredményeket 28 éves korában közölte és 36 éves volt, amikor meghalt. Hátramaradt iratai azt bizonyítják, hogy később a hőanyagelmélettel szakított, felfogása jelentősen fejlődött, azonban korai halála nem engedte, hogy vizsgálatait befejezze.
Carnot munkájának megjelenése után tíz, halála után két évvel jelenik meg Clapeyron dolgozata (1834), amely Carnot eredményeit matematikai formába önti, anélkül, hogy ezekhez fizikai szempontból bánni lényegeset hozzátenne.
Carnot és Clapeyron munkáit tanulmányozva a mai olvasó rendkívül erősen érzi azt a hiányt és bizonytalanságot, amely az energiatétel nemismeréséből származik. Ezekben a munkákban burkoltan már benne van az entrópia‑fogalom, de az abszolút hőmérséklet és entrópiaskála felismerése az energiatétel felhasználása nélkül lehetetlen. Az ideális gáz entrópiáját Poisson tulajdonképpen már 1823‑ban ismerte, midőn az adiabataegyenletet:
$$p\cdot V^{\kappa }=\mathrm{állandó}\ \ \ \ (\kappa =\mathrm{konstans})$$
meghatározta.$^3$ (Maga az "adiabatikus" elnevezés nem Poissontól, hanem Rankine‑től szarmazik.) Mégis, Poisson nagyon messze volt attól, hogy az entrópiafogalmat ebben a speciális esetben is felismerje. Ez ismételten azt a hiányt mutatja, ami a hőelméletben az energiatételt illetően uralkodott.
Az energiatétel kialakulásának körülményeivel itt nem foglalkozhatunk részletesen, mivel a probléma jelentősen túlvezet a hőelmélet keretein. Ezúttal a fenti példák kapcsán csupán arra kívánunk rámutatni, hogy az energiatétel felfedezése a fizika és különösen a hőelmélet fejlődésében már tisztán elméleti szempontból is szükségszerű volt. A kutatók minduntalan olyan nehézségekbe ütköztek vizsgálataik kapcsán, melyek megoldására irányuló törekvésük az energia megmaradásának elve felé irányította figyelmüket. Másrészről viszont az is igaz, hogy magát az elméletet a gyakorlati szükségletek sarkalták a további fejlődésre. Az 1840‑es években már teljesen tarthatatlan volt az az állapot, hogy a nagy gyakorlati jelentőségre szert tett gőzgépek úgyszólván minden elméletet - gyakorlatilag hasznosítható elméletre gondolok - nélkülöznek.
A fennálló sürgető igény következménye, hogy egyszerre több helyen és egymástól függetlenül oldották meg a problémát. Ezzel kapcsolatban elegendő Mayer, Joule és Helmholtz nevére utalni. Szükségszerűen felvetődik a kérdés, mi az a tényező, ami ezt a rendkívül világos és áttekinthető, tehát könnyen megérthető tételt mégis olyan nehezen elérhetővé tette. Azt hiszem nem tévedek, ha ezért a fizikában uralkodó ideológiai zűrzavart teszem felelőssé. Zavarólag hatott egyrészt a mechanisztikus materialista felfogás, melynek materialista volta abban állott, hogy egy‑egy újabb jelenséget mindig egy‑egy újabb imponderabiliummal hozott kapcsolatba (hőanyag, elektromos és mágneses fluidum stb.). A zavar másik forrását az erőfogalom idealista értelmezésében kell látnunk. Galilei és Newton munkáiban, a mechanikát illetően világos az erő fogalmának jelentése: az erő az impulzusátadással járó kölcsönhatás mértéke. Az erő nem mozgatóerő, a mozgás önmagát is fenntartja; a mozgási állapot megváltoztatásához van szükség erőhatásra. Galilei és Newton tudományos eredményei tehát semmi alapot nem adnak arra, hogy az erőt függetlenítsék az anyagtól. Az erő és az anyag szétválasztása egy későbbi egészségtelen, a valóságtól elszakadt spekuláció szüleménye. (Ami az erőtereket illeti, ezek mindig valamilyen konkrét anyagi rendszerrel kapcsolatban lépnek fel, sőt a modern fizika felfogása szerint maga az erőtér is anyagi realitás.) Életerő, hőerő, vegyierő stb. olyan fogalmak és olyan értelemmel bírnak ebben az időben, hogy magáról a mozgó anyagról helytelen irányba elterelik a figyelmet. Tehát abban sem túlozunk, ha azt állítjuk, hogy az energia megmaradása elvének felfedezése ill. a felfedezés előkészítése nem tisztán fizikai, hanem filozófiai kutatás is volt. Végül nehézséget okozott az a körülmény, hogy az impulzustétel és az energiatétel két különböző megnyilvánulási formája lévén az anyag általános mozgástörvényének, minduntalan összekeveredett és ez a keveredés ellentmondásokra vezetett. Az impulzustételt ekkor már régen ismerték, az energia megmaradásának egyes eseteit pedig, melyek a kutatásban felszínre kerültek, erőmegmaradási elvként, mintegy az impulzustételbe igyekeztek beolvasztani. Tanulságul és illusztrációként egy idézetet iktatok be Mayer két leveléből, amelyeket 1841‑ben Baur matematikus barátjához intézett:$^4$
"A vegyésznek az az alapelv az irányítója, hogy maga a »szubsztancia«, az anyag lényege, elpusztíthatatlan és hogy az alkotó elemek a létrejött összetétellel a legszükségszerűbb vonatkozásban állanak: ha $\mathrm{H}$ és $\mathrm{O}$ eltűnik (minőségileg elértéktelenedik), és $\mathrm{HO}$ lép fel, a kémikusnak nem szabad azt feltételeznie, hogy $\mathrm{H}$ és $\mathrm{O}$ tényleg semmivé lett s $\mathrm{HO}$ véletlenül kívülről képződött; ennek a tételnek szigorú érvényesítésén épül fel az újabb kémia, amely nyilvánvalólag csak így vezethetett határozott eredményekhez."
"Az erőkre is ugyanezeket az alapelveket kell alkalmaznunk; szintén elpusztíthatatlanok, mint a szubsztancia, szintén kombinálódnak egymással, régi alakjukat elvesztik (mennyiségileg semmivé lesznek), új formában lépnek fel s a régi és új formák összefüggése éppoly lényeges, mint a $\mathrm{H}$ és $\mathrm{O}$ s a $\mathrm{HO}$ között. Az erők (amelyeknek szigorúan tudományos kifejlődését nem fogom magyarázatlanul hagyni) mozgásból, villamosságból és melegből állanak."
A másik levélben ezt írja: "A fizika törvényeit ellentétben a kémiával nagymértékben egyszerűsíti az a körülmény, hogy a különböző erők egymásra vezethetők vissza: mennyire örültem, amikor erre az eredményre, az erők egyenlő megoszlására fokozatosan rábukkantam! A kémikusnak elvi feltevésének keresztülviteléhez tudnia kell, hogy $\mathrm{H+O}$ annyi mint víz, és így tovább, minden esetben, akár összetételről, akár felbontásról van szó; éppúgy kell a fizikusnak tudnia, hogy $\mathrm{+M(otus)-M=C(alor)}$.
$$\mathrm{+M(otus)-M=C(alor)}$$
Miután minden földi mozgás ellenállást (azaz M minőségileg való megsemmisülését) eredményez, a hő azonban minden testet kiterjeszt, vagyis a test $\mathrm{+M}$ és $\mathrm{-M}$‑é esik szét, itt az erők olyan játékával találkozunk, amely a tökéletes egyensúly helyreállításáig tart." Mayernek ez utóbbi megjegyzései arra utalnak, hogy rugalmatlan ütközéskor $+mv$ és a $-mv$ impulzusok látszólag megsemmisítik egymást és szerinte ebből származik a hő. A fogalomzavar világos; a folyamat első részét az impulzustétel, második részét pedig az energiatétel szerint értékeli. A tévedés közvetlen előidézője az, hogy a mechanikai impulzustétel, mint régen megállapított törvény adva van számára, másrészt a hőjelenségekben maga az impulzustétel kifejezetten egyáltalán nem játszik szerepet. A hőelmélet kizárólagosan energetikai diszciplína.
A fogalmak nem megfelelő helyen való használata Mayert ellentmondásokba keverte. Így pl. a gravitációs tér potenciális energiájának és belőle nyerhető mozgásnak kapcsolatát kezdetben az
$$m\cdot g\cdot h=m\cdot v$$
formulával írja le. Később főként barátjának, Baurnak segítségével ezeket az ellentmondásokat fokozatosan kiküszöbölte és megtalálta a helyes kapcsolatot
$$m\cdot g\cdot h=\frac{1}{2}mv^2$$
Ugyanezeken a nehézségeken a Mayer előtti kutatók még inkább átestek (ill. beleestek), és a fellépő ellentmondások megakasztották őket további kutatásaik folytatásában. Az előbbi keletű "eleven erő" elnevezés (a kinetikus energia helyett), valamint az, hogy maga Helmholtz is az "erő megmaradásának" elvéről beszél, szintén árulkodó tünetek a jelzett fogalmi zavart illetően. Néhány évvel később Thomson már felismerte a mozgástörvényekben uralkodó kettősséget és az impulzus és erő elnevezések mellett bevezette az energia szó használatát. Ezzel az energiatétel világosan kimondott és az impulzustételtől élesen elkülönített megállapítássá vált, miáltal a tudományos kutatásban hatóképessége is jelentősen megnövekedett.
Az $mv$ mozgásmennyiség és az $\displaystyle \frac{1}{2}mv^2$ mozgási energia fenti megkülönböztetése az eddigi okfejtés alapján talán nem tűnik elég meggyőzőnek. Hogy a mozgásmennyiség a testnek valóban lényegesen más tulajdonsága, mint az energia, az a következőkből látszik világosan. Tekintsük két azonos $m$ tömegű golyó rugalmas centrális ütközését: a két golyó ütközés előtt és után ugyanazon közös egyenes mentén mozog; ütközés előtti sebességük legyen $v_1$ ill. $v_2$, az ütközés utáni pedig $c_1$ ill. $c_2$. A mozgásmennyiség megmaradásának tétele szerint az ütközés előtti mozgásmenynyiség
$$mv_1+mv_2$$
egyenlő az ütközés utánival
$$mc_1+mc_2$$
azaz
$$mv_1+mv_2=mc_1+mc_2$$
és $m$‑mel átosztva
$$v_1+v_2=c_1+c_2\tag{1} \label{eq:(1)}$$
Az energia megmaradásának elve szerint az ütközés előtti mozgási energia
$$\frac{1}{2}mv^2_1+\frac{1}{2}mv^2_2$$
és az ütközés utáni
$$\frac{1}{2}mc^2_1+\frac{1}{2}mc^2_2$$
szintén egyenlők egymással, azaz
$$\frac{1}{2}mv^2_1+\frac{1}{2}mv^2_2=\frac{1}{2}mc^2_1+\frac{1}{2}mc^2_2$$
Innen, $\displaystyle \frac{1}{2}m$‑mel való osztás után
$$v^2_1+v^2_2=c^2_1+c^2_2\tag{2} \label{eq:(2)}$$
Egyenlő tömegű és közös egyenes mentén mozgó golyók ütközésekor tehát az $\eqref{eq:(1)}$ összefüggés írja le a mozgásmennyiség és a $\eqref{eq:(2)}$ az energia megmaradását. Amennyiben ismerjük az ütközés előtti $v_1$ és $v_2$ sebességeket, úgy ezek segítségével és a jelzett két egyenlet felhasználásával kiszámíthatjuk az ütközés utáni $c_1$, és $c_2$ sebesség értékét. A számítás igen egyszerű. Az $\eqref{eq:(1)}$ összefüggés ugyanis így írható
$$v_1-c_1=c_2-v_2\tag{1a} \label{eq:(1a)}$$
a $\eqref{eq:(2)}$ pedig
$$v^2_1-c^2_1=c^2_2-v^2_2$$
azaz
$$(v_1+c_1)(v_1-c_1)=(c_2+v_2)(c_2-v_2)$$
Osszuk el az utóbbi egyenletet $\eqref{eq:(1a)}$‑val, akkor
$$v_1+c_1=v_2+c_2\tag{3} \label{eq:(3)}$$
Az $\eqref{eq:(1a)}$ és a $\eqref{eq:(3)}$ egyenletek összeadásával nyerjük mármost, hogy
$$2v_1=2c_2$$
$$v_1=c_2$$
továbbá $\eqref{eq:(1a)}$‑nak $\eqref{eq:(3)}$‑ból való kivonásával
$$2c_1=2v_2$$
$$c_1=v_2$$
Ez azt jelenti, hogy ütközéskor az egyenlő tömegű golyók sebességet cserélnek. Számunkra azonban most az a lényeges, hogy $v_1$ és $v_2$ ismerete alapján az energia és a mozgásmennyiség megmaradási elvének felhasználásával $c_1$ és $c_2$ kiszámítható. A két megmaradási elv ugyanis a két ismeretlen meghatározására két egyenletet szolgáltat. Vegyük észre, hogy egyik megmaradási elv önmagában csak egy egyenletet jelent, amelyikből a két ismeretlen nem határozható meg. Mindez azt jelenti, hogy a mozgásmennyiség és az energia megmaradásának elve nem azonosak, hanem kiegészítik egymást. Természetesen, mindaddig, míg a két elvnek megfelelő mennyiségi kapcsolatokat fel nem írjuk, ezt nem könnyű észrevenni. Nem csodálkozhatunk tehát azon, hogy kezdetben a két fogalmat összekeverték.
A "hő" és a "mozgás" viszonyának pontos megértéséhez részletesen foglalkoznunk kell a súrlódás jelenségével. A sima asztallapon meglökött tárgy egyre lassuló sebességgel mozog, míg végre megáll, Hogy mi történik az energiával, az világos. A tárgyon - a meglökéskor - munkát végzünk, aminek következtében bizonyos mozgási energiára tesz szert. Ha $W$ a végzett munka, $m$ a tárgy tömege, és $v_0$ a kezdeti sebessége, akkor kezdetben
$$W=\frac{1}{2}mv^2_0$$
A súrlódás következtében a tárgy mozgási energiája egyre kisebb lesz, megfelelően az eredetileg nyert $v_0$ sebesség mind kisebb $v$ sebességbe megy át. Az energia azonban nem vész el, hanem az egymáson súrlódó testek belső energiájává alakul át, ami közvetlenül a testek hőmérsékletének emelkedésében jut kifejezésre. Ha bizonyos $v$ sebesség mellett $E$, végül pedig $E_0$ a belső energia növekedése, úgy a teljes energiamérleg a folyamat különböző szakaszaiban így alakul
$$W=mv^2_0=\frac{1}{2}mv^2+E= E_0$$
Azt mondottuk, hogy energia és mozgásmennyiség különböznek egymástól, külön‑külön megmaradási tétel érvényes rájuk. Mi történik tehát súrlódás közben a mozgásmennyiséggel? Vegyünk figyelembe minden testet, amely részt vesz a folyamatban. Ezek: a meglökött tárgy, valamint az asztal, amely a földhöz képest rögzítettnek tekinthető. Az asztal és a Föld együttes tömegét jelöljük $M$‑mel, amely az $m$ tömegű tárgy partnere a szóban forgó folyamatban. A kezdeti állapot a földön nyugvó megfigyelő számára az, hogy hozzá képest mind a Föld, mind a tárgy nyugalomban van, tehát e megfigyelő szempontjából mindkét tárgy mozgásmennyisége zérus, így összegük is az. Midőn a testünkben felgyűlt kémiai energia rovására a tárgyon munkát végzünk (ti. $v_0$ sebességgel mozgásba hozzuk) $m\cdot v_0$ mozgásmennyiséget közlünk vele. A mozgásmennyiség látszólag semmiből keletkezett, hiszen - mint mondottuk - kezdetben az egész rendszer mozgásmennyisége zérus volt. Látszólag valóban az a helyzet, mintha mozgásmennyiség keletkezett volna. Vegyük azonban figyelembe a többi partnert is (Föld, mozgást elindító személy, asztal), ti. nemcsak az asztal stb. hat a tárgyra, hanem a tárgy is visszahat a többi együttesére. E visszahatás eredményeként a másik (azaz $M$ tömegű) partner is nyer mozgásmennyiséget, és így sebességet is. Legyen ez a sebesség $V_0$. Mivel az összes mozgásmennyiség eredetileg zérus volt, a két partner összes mozgásmennyisége mindvégig szintén zérus, tehát
$$mv_0+MV_0=0$$
Innen
$$V_0=-\frac{m}{M}v_0$$
amiből látszik, hogy a sebességek ellenkező irányúak, és az is látszik, hogy a Föld eme ellentétes irányú sebessége annyiszor kisebb, ahányszor $M$ tömege nagyobb a tárgy $m$ tömegénél. Mivel az $\displaystyle \frac{m}{M}$ tömegviszony elképzelhetetlenül kicsiny, igen kicsiny a $V_0$, visszalökődési sebesség is. Gyakorlati szempontból a $V_0$ elhanyagolható, a mozgásmennyiség megmaradásának szempontjából azonban nem. A továbbiakban ahogyan $v_0$ a súrlódás folytán $v$-re csökken, ugyanúgy kell bizonyos $V$‑re csökkennie a $V_0$‑nak is. így a folyamat különböző szakaszait tekintve a mozgásmennyiség "mérlege" a következő:
$$0=mv_0+MV_0=mv+MV=0$$
Látjuk tehát, hogy az energia és a mozgásmennyiség külön‑külön állandó marad, bár a folyamatbeli változások jellege más az energia és más a mozgásmennyiség átalakulása szempontjából. Hővé nem a mozgásmennyiség, hanem a mozgási energia alakul át. Amíg e megkülönböztetést nem tudták megtenni, nem tudták a folyamatok energiamérlegét sem felírni. Enélkül viszont, mennyiségi viszonyaiban nem ismerhették fel az energiatételt.
Galilei (1564‑1642), Descartes (1596‑1650), Hooke (1635‑1703) és végül Newton (1642‑1727) munkásságának eredményeként tisztázódott a mozgásmennyiség fogalma és a kapcsolatos megmaradási tétel. E fizikai tétel általánosításaként egyre több filozófus vallotta a mozgás elpusztíthatatlanságát állító filozófiai tételt. A tisztának látszó helyzetet Leibniz (1646‑1716) zavarta meg, felismerve azt a további tényt is, hogy munkavégzéskor a testek bizonyos "eleven erő"‑re tesznek szert, mégpedig: meghatározott értékű munka mindig ugyanannyi "eleven erő"‑t hoz létre. Az "eleven erő" nem más, mint a mozgási energia, Leibniz tehát ebben a vonatkozásban - bár csak a mechanikára vonatkozóan - az energia megmaradásának elvét ismerte fel. Mindez érdeme Leibniznek, hibája azonban az, hogy tételét a mozgásmennyiség megmaradásával akarta indokolni: a kétféle fogalmat összekeverte. Ebből igen áldatlan vita keletkezett. A fizikusok és filozófusok egy része az $mv$‑t (mozgásmennyiséget), más része az $\displaystyle \frac{1}{2}mv^2$‑t (mozgási energiát) tekintette a mechanikai mozgás mértékének. Mayer (1814‑1878) és Helmholtz (1821‑1891) mutattak rá, hivatkozva a megfelelő tényanyagra, hogy a mozgásmennyiség $(mv)$ és az "eleven erő" $\left(\displaystyle \frac{1}{2}mv^2\right)$ különböző jellegű mennyiségek. Ezt követően kezdett tisztázódni a helyzet. Midőn Engels a természet dialektikájával kezdett foglalkozni, az energiatétel még nem vált tudományos közkinccsé, így a mechanikai mozgás mértékének problémája is fennállott. Engels éleslátására vall, hogy a korabeli tudományos irodalomban meglevő ellentmondást észrevette. Észrevételeit a "A mozgás mértéke - Munka" c. tanulmányában$\large{^\ast{}^\ast}$ rögzítette le (l. Engels: A természet dialektikája).
Az energia megmaradása elvének egyik fontos következménye az örökmozgó, perpetuum mobile lehetetlensége. Örökmozgónak lehetne nevezni egy olyan szerkezetet, amely energia felhasználása nélkül végezne munkát. Tekintve azonban, hogy a köznapi értelemben vett munkavégzés nem egyéb, mint energiaátvitel, energia nélkül munka sem lehetséges; ha a rendelkezésre álló energiaforrás kimerül, a munkavégzés is leáll. Az energia megmaradásának elve szinte a természet minden jelenségében közvetlenül megnyilvánul, így a felismerés annyira alapvető, hogy a perpetuum mobile létezését feltétlenül el kell vetnünk. A későbbiekben a perpetuum mobile fogalma más vonatkozásban is felmerül. Éppen ezért, az olyan örökmozgót, amely az energiatétellel ellentmondásban végezne munkát, I. fajú perpetuum mobilénak szokták nevezni. Idők során felmerült olyan gép gondolata is, mely ugyan az energia megmaradásának elve alapján, de az entrópiatétel megszegésével működne. Bizonyos értelemben ezt is örökmozgónak lehet nevezni, megkülönböztetésül azonban a II. fajú perpetuum mobile elnevezést kapta. A megfelelő helyen ezzel a kérdéssel is részletesen foglalkozunk.
5. Az entrópiafogalom megszületése
Az entrópia születésének időpontját nem lehet egyértelműen meghatározni. Annyit mondhatunk csupán, hogy az entrópia kb. 100 éves. A hőelméletnek fontos részleteredményei születtek meg az energia megmaradása elvének világos és tudatos kimondása előtt. Ezekben az eredményekben több helyen nyomát találjuk az entrópiafogalomnak is. A részleteredmények, miként egy épület előregyártott elemei tehát már készen vannak: de hiányzik az összefogó erő, amely egységes épületté, egységes tudományos rendszerré kovácsolja össze az egyes tudományos részleteket. Az összefogó erő és rendszerező elv: az energia megmaradásának tétele. Ennek felismerésétől kezdve (amit kb. 1848‑50 tájára tehetünk) néhány év alatt rohamosan épül egységes átfogó elméletté a termodinamika.
Az egységes elmélet tető alá hozásában két fizikusnak van nagy szerepe : Thomsonnak (a későbbi Lord Kelvin, 1824‑1907) és Clausiusnak (1822-1888). Az 1850‑es évek hatalmas fellendüléssel megindult munkáját igen nehéz áttekinteni. Ekkor vezeti be Thomson a belső energia fogalmát (mechanikai energia). 1851‑ben Zeuner a "belső hő" elnevezést használja. Maga a belső energia elnevezés Clausiustól (1864) származik.
Kezdetben Clausius és Rankine (1820‑1872) a belső energiát, két részből összetettnek tekintik: "wirkliche Wärme" ("valódi hő", $dH$) és "merkliche Wärme" ("látszólagos hő", $dI$). Jelöljük $dW$‑vel az elemi munkát. A termodinamika első főtétele$^5$ szerint:
$$dQ=dE-dW=dH+dI-dW$$
A $dI-dW$ mennyiséget "diszgregatív" munka elnevezéssel jelölték. Ebből a szétválasztásból nőtt ki a későbbi "hasznos" és "szabad" energia fogalma.
A reverzibilitás és irreverzibilitás problémáját$^6$ Thomson veti fel (1852‑53), felismerve az energiadisszipáció jelenségét. Az entrópia értelmezése éppen ezzel kapcsolatban történik. Clausius mértéket keres a körfolyamatoknál történő energiadisszipációra, így jut el az entrópiafogalomhoz. Kimutatja (1854), hogy egy körfolyamat esetében, melyet izoterm és adiabatikus szakaszpárokból képzelünk összetettnek, fennáll, hogy
$$\sum\limits_{(i)}\frac{Q_1}{T_1}=0$$
A $\displaystyle \frac{dQ}{T}=d\varphi $, ill. a $\varphi $ mennyiséget kezdetben: "Aequivalenswert'',$^7$ "Verwandlungswert"$^8$ (Clausius), "termodinamikai függvény" (Rankine) elnevezésekkel jelölték. A második főtételt ebben az időben Clausius gyakran "az átalakulások aequivalenciája törvényé"-nek (Satz von der Aequivalens der Verwandlungen) nevezi. Az entrópiafogalom szinte észrevétlenül lép itt színre, a figyelem nem rá, inkább következményeire irányul, aminek jellegzetes tünete a használt sokféle elnevezés is. Maga az entrópia elnevezés csupán 90 éves. A német‑görög szótár szerint
die Verwandlung$^9$ = ἐν τροπή
Ebből a germánosított Entropie, innen pedig a latinosított entrópia szó származik.
A fogalom jelentőségének és szerepének felismerése ezzel kezdetét vette. Clausius egy Annalen der Physik und Chemie‑beli dolgozatában$\large{^\ast{}^\ast{}^\ast}$ utal arra, hogy a világegyetem entrópiája a maximum felé törekedvén, a világegyetem a termodinamikai egyensúly állapota felé tart. Az azóta "hőhalál"‑nak nevezett (termodinamikai egyensúlyra) vonatkozó nézetét Clausius két évvel később (1867) fejti ki részletesen egy népszerű előadásban.
A Clausius‑féle (az irreverzibilis folyamatok törvényszerűségeit is kifejtő) törvény molekuláris‑kinetikus értelmezése és levezetése első ízben id. Szily Kálmánnak sikerült. Az említett kapcsolat a múlt században külföldön is mint Clausius‑Szily‑féle törvény szerepelt. A "kinetikus elmélet" elnevezés arra utal, hogy a molekulákból álló rendszer egészének jellemzőit a rendszert alkotó molekulák adataira alkalmazott klasszikus mechanikai egyenletekből statisztikai közepelési eljárással nyerjük. A múlt század végi szerzők ilyen esetekben csak a mechanikai alapot hangoztatták, a statisztikus módszert, pedig hangoztatás nélkül egyszerűen csak felhasználták. Így tett Szily is. Módszere statisztikus és nem tisztán mechanikai. Eredménye pedig jelentős fejlődést jelentett a maga idejében, méltán lehetünk rá büszkék. Hazai vonatkozásban másik említésre méltó tudós Farkas Gyula, aki a II. főtétel axiomaikus megalapozásában végzett úttörő munkát. (Carathéodoryt 14, Ehrenfest‑Afanasjevát pedig sok vonatkozásban 30 évvel megelőzte.)
A vázolt, szinte csak időrendi felsorolás önmagában is bír némi érdekességgel, de természetesen nem tart igényt arra, hogy az entrópia fogalmi megalapozását helyettesítse. Most azonban valóban itt az ideje, hogy közelebbről megismerkedjünk magával az entrópiával és az entrópiatétellel.
II. AZ ENTRÓPIA ÉS AZ ENTRÓPIATÉTEL SZEREPE A HŐELMÉLETBEN
A természetben és a technikai eszközök működése közben végbemenő folyamatok egyik alapvető sajátosságára kívánjuk a következőkben felhívni a figyelmet. Különböző jelenségeket veszünk vizsgálat alá és megkeressük a közös törvényszerűséget.
Elsőnek foglalkozzunk a hőanyagelmélet kapcsán már tárgyalt közlekedőedényekkel. Láttuk, hogy az egymással közlekedésben levő edények folyadéktartalma oly módon áramlik egyikből a másikba, hogy ezáltal a különböző edényekben a szintkülönbség kiegyenlítődjék. E jelenség mélyebb oka az, hogy a folyadékoszlopok egymásra nyomást gyakorolnak és végső fokon a nyomáskülönbségek egyenlítődnek ki. A folyadékoszlop viszont a Föld nehézségi erőterében elfoglalt helyzete és ezzel járó súlya folytán rendelkezik ún. hidrosztatikus nyomással. Ha a folyadék nincs edénybe zárva, igyekszik szétterülni, ill. azokat a helyeket megkeresni, ahol közelebb van a Föld középpontjához. Ugyanez a jelenség lép fel akkor is, amikor az elmálló szikladarab legurul a völgybe, a folyóvíz pedig alacsonyabb fekvésű helyek felé veszi útját. Ha mármost gondolatban minden egyéb ható tényező szerepét kikapcsoljuk, világosan látjuk, hova vezetnek az említett jelenségek. A Föld felszínén lassan eltűnnek az egyenetlenségek, a szintkülönbségek kiegyenlítődnek, éppúgy, ahogy a tengerek vizének felszíne is a nehézségi erőhatás által megszabott felülettel határolódik. A Föld középpontjától különböző távolságban ugyanaz a test különböző nagyságú helyzeti energiával rendelkezik. Egy megállapodásszerűen választott test helyzeti energiája magát az erőteret jellemzi és az erőtér potenciáljának szokták nevezni. Végeredményben a fenti példák mindegyikében az történik, hogy a különböző potenciálú helyeken levő testek potenciálkülönbsége kiegyenlítődni igyekszik.
Teljesen hasonló törvényszerűséget tapasztalunk az elektromosság áramlásánál, röviden; az elektromos áram tanulmányozása közben is. Az elektromos áram az elektromos feszültség fennállásának következtében jön létre és mindaddig tart, míg a feszültségkülönbség ki nem egyenlítődött. A villámcsapás például a felhők és a Föld közötti elektromos feszültségkülönbség kiegyenlítődésére szolgál.
A felfújt gumilabdába ill. léggömbbe zárt nagy nyomású levegő igyekszik utat találni magának: a labda, ill. léggömb előbb‑utóbb szétpukkan és a nagy nyomású levegő a kisebb nyomású felé hatol, míg végül a kezdeti nyomáskülönbség kiegyenlítődik. A légkörben fennálló nyomáskülönbségek szintén kiegyenlítődni igyekeznek: a levegő a nagy nyomású helyről a kisebb nyomás felé áramlik, mindaddig, míg a nyomáskülönbségek ki nem egyenlítődnek.
A víz elpárolgása és lecsapódása szintén az előbbiekhez hasonló kiegyenlítődési folyamat. Minden kémiai anyagnak van egy olyan jellemző tulajdonsága, az ún. kémiai potenciál, amely kiegyenlítődni igyekszik. A folyékony víz mindaddig párolog, azaz gőzállapotba megy át, míg a fölötte levő vízgőz kémiai potenciálja kisebb, mint a folyékony állapotú vízé. Fordítva: ha a folyékony állapotú víz kémiai potenciálja kisebb, mint a légnemű állapotúé, a gőz lecsapódik. Ez történik pl. az eső, harmathullás stb. alkalmával.
Mint a hőanyagelmélettel kapcsolatban említettük, a természetben fennálló hőmérsékletkülönbségek szintén kiegyenlítődni igyekeznek. Ha melegedni akarunk, úgy az előző környezetnél magasabb hőmérsékletű helyet keresünk; a melegítendő vizet a felforrósított tűzhelyre tesszük. Hasonlóképp: hűtésnél alacsonyabb hőmérsékletű testtel hozzuk érintkezésbe a lehűtendő testet. Mind e jelenségek lényege a hőmérséklet‑kiegyenlítődés.
A felsorolt egyes jelenségek felismerhetően közös törvényszerűségnek különböző esetekben való megnyilvánulásai. Ez az általános törvényszerűség a következő:
Az anyagi testek közt végbemenő energiacserék és energiaátalakulások közvetlen előidézője valamilyen kölcsönhatás, melynek főbb típusai a fentiek szerint:
- mechanikai (közlekedőedények, szél stb.)
- elektromos (elektromos áram)
- anyagi kölcsönhatás, fázisátalakulás (párolgás, lecsapódás, fagyás és olvadás stb.)
- hőhatás (felmelegedés, lehűlés)
Ezeken kívül természetesen sok más kölcsönhatási fajta is ismeretes (pl. mágnesezés), melyekkel azonban most nem foglalkozunk. Igen alapvető tény, hogy mindegyik kölcsönhatáshoz tartozik egy‑egy tulajdonság (ún. intenzitásmennyiség), amely a kölcsönhatást minden vonatkozásban jellemzi. A kölcsönhatások és a hozzájuk tartozó intenzitásmennyiségek a következők:
| Kölcsönhatás | $\ \ $Jellemző intenzitásmennyiség$\ \ $ |
$\ \ $Mechanikai $\ \ $Elektromos $\ \ $Anyagi $\ \ $Hőhatás | nyomás, feszültség elektromos potenciál kémiai potenciál hőmérséklet |
Az egyes kölcsönhatásokat jellemző közös törvényszerűség abban áll, hogy egyrészt: a testek mindaddig egyensúlyban vannak egymással, amíg a megfelelő intenzitásmennyiségek értéke az egymással érintkező testekben azonos értékű; másrészt, ha a megfelelő intenzitásmennyiségek értéke különböző, egyik testről a másikra energia áramlik át, éspedig az energia áramlás mindig olyan irányú, hogy a kiegyenlítődést, tehát az egyensúly beállását segíti elő.
Tehát: az energiaátadási folyamatok mindig kiegyenlítődési folyamatok és sohasem fordított irányúak. Konkrétan: az energiaátadás a hőmérséklet-, nyomás- stb. különbség megszüntetésére és nem előidézésére törekszik. A tűzhelyre tett víz bizonyára melegedni fog és nem hűlni; a jégre tett test pedig bizonyára lehűl és nem melegszik fel, közben még alacsonyabb hőmérsékletre hűtve a jeget.
Mindez azt mutatja, hogy a hőanyagelméletben valóban helyes volt a hőmérsékletkülönbségek kiegyenlítődésének felismerése, de tévesen gondolták azt, hogy a kiegyenlítődés közben valamilyen hőanyag áramlik egyik testről a másikra. Helyesen felfogva a jelenség lényegét, nem hőanyag, hanem energiaátadásról kell beszélnünk. Ezzel némileg tisztázódtak fogalmaink, egyúttal azonban további nehézségekkel kerültünk szembe. A hőanyagelmélet szerint ugyanis a hőanyag áramlása csakis a hőmérsékletkülönbségtől függött, a modern hőelmélet szerint viszont az energiaátadás nemcsak a hőmérsékletben, de valamennyi intenzitásmennyiségben fennálló különbségtől függ. Gondoljunk megint a közlekedőedényekre. Tekintsük a testeket jelképes edényeknek, melyek mindegyikében energia van felhalmozódva. Mármost a fent mondottak szerint, egy‑egy "edény"‑hez többféle értelemben vett "szintmagasság" tartozik és két egymással érintkező edény csak akkor lehet egyensúlyban, ha már mindenfajta "szintmagasság" kiegyenlítődött. Mindez kis képzelőerővel még megérthető, azonban az alábbi körülmény további bonyodalmat okoz:
Az egyik testből a másikba átáramlott energia végső fokon csak az energiamennyiséget szaporítja (ill. csökkenti), de az nem tűnik ki, hogy milyen fajtájú kölcsönhatás révén került a testbe (ill. távozott abból). Más szóval ez azt jelenti, hogy például a hőmérséklet‑kiegyenlítődés közben nyert (vagy vesztett) energia, ill. maga az energiaváltozás a többi intenzitásmennyiség megváltozását is maga után vonhatja; a különböző kiegyenlítődési folyamatok egymást befolyásolni képesek. E kölcsönös zavarást a hőelméletben "kereszthatás"‑nak (kereszteffektusnak) nevezik. Az utóbbi két évtized vizsgálatai ezek törvényszerűségeit is kiderítették. Az említett törvényszerűségek rövid ismertetésének érdekében nézzük meg még egyszer azt az esetet, amikor csak egy intenzitásmennyiségben áll fenn különbség és amikor egyúttal arról is gondoskodtunk, hogy a többi intenzitásmennyiség értéke a folyamat közben ne változhasson meg.
Rajzoljuk fel pl. az ilyen tiszta hőmérséklet‑kiegyenlítődés menetét grafikusan (1. ábra). A vízszintes legyen az időtengely, a függőleges pedig a hőmérsékleti értéket feltüntető tengely. A két test közötti $\Delta T$ hőmérsékletkülönbség időbeli csökkenésének menete vázlatosan a következő:

Mármost, ha a különböző fajta kiegyenlítődési folyamatok nem befolyásolnák egymást, valamennyi intenzitásmennyiségben fennálló differencia külön‑külön, egymástól függetlenül, hasonló törvényszerűség szerint fokozatosan, egyenletesen csökkenve tartana zérushoz. Vagyis hőmérséklet-, nyomás-, stb. különbségek egyidejű fennállása esetén mind a hőmérséklet-, mind a nyomás- stb. beli különbségek "lecsengése" a fenti grafikon szerint történne.
Mivel azonban a különböző fajta közelhatások ill. a megfelelő kiegyenlítődési folyamatok egymást kölcsönösen befolyásolják, a folyamat a valóságban bonyolultabb lesz a fent jelzettnél. Előfordulhat pl. hogy a $\Delta T$ hőmérséklet- és $\Delta p$ nyomáskülönbség egyidejű lecsengése a 2. és 3. ábrán bemutatott módon zajlik le:

Vagy előfordulhat pl., ha $\Delta p=0$ volt eredetileg, úgy $\Delta T$ csökkenése közben a $\Delta p$ véges értéket vesz fel, és csak azután csökken le megint zérusra (4. ábra.):
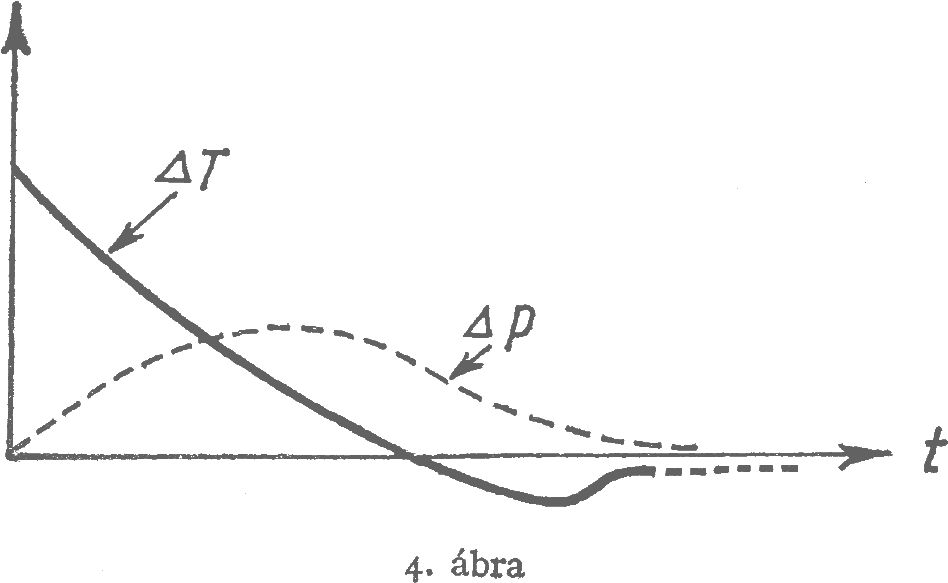
A kereszthatások eme jellegzetességére még több vonatkozásban visszatérünk. Most még csak egyetlen, de igen lényeges mozzanatot említünk. Bárhogyan is történjék az intenzitásparaméterek különbségének kiegyenlítődése, a teljes egyensúly elvileg véges időn belül sohasem áll be. A rendszer ugyan egyre közelebb és közelebb kerül az egyensúlyi állapothoz, de teljesen sohasem éri el. (Ahogyan a hiperbola asszimptótáját is a hiperbola egyre jobban megközelíti, de teljesen el sohasem éri.)
Amit a fentiekben elmondottunk, az nem más: maradéktalanul maga az entrópiatétel. Meglepő lehet, hogy az entrópiatételben magáról az entrópiáról szó sem esett. A tétel azonban jelentésében teljesen világos, csupán azt nem értjük még, mi köze az entrópiához? A továbbiakban erre is választ adunk.
Az eddigiek során megállapítottuk, hogy a természetben végbemenő folyamatok mindig felfoghatók a természetet alkotó fizikai rendszerek közötti kölcsönhatásokként, amelyek mindig felületről‑felületre terjednek tova (és sohasem úgy, hogy egy hatás valahol fellépvén, annak következménye bármilyen távolságban ugyanabban az időpontban jelentkezik). Kizárólag csak közelhatások vannak, s ezek típusai: mechanikai, hőhatás, elektromos hatás, anyagi hatás; e közelhatások mindegyikéhez tartozik egy‑egy tulajdonság, amelyet jellemző intenzív mennyiségnek neveztünk. A mechanikai közelhatásnak megfelel, mint intenzív mennyiség, a negatív előjelű nyomás, a mechanikai feszültség; a hőhatásnak: a hőmérséklet; az elektromos hatásnak: az elektrosztatikus potenciál; az anyagi hatásnak: a kémiai potenciálok. Ezek jellemzik a közelhatásokat olyan módon, hogy két vagy több test egyensúlyban van egymással akkor, ha a megfelelő intenzív mennyiségek egyenlőek: ha a rendszer minden egyes részében ugyanakkora a feszültség, nyomás, hőmérséklet, elektromos ill. kémiai potenciál, vagyis, ha a rendszeren belül nincsenek potenciálkülönbségek. Ezeket a potenciálkülönbségeket lehet affinitásnak, rokonságnak, a változásra való törekvés mértékének tekinteni. Egy rendszer tehát egyensúlyban van, ha az affinitások értéke nulla, vagyis ha az intenzív mennyiségek szempontjából a testek homogének. A kémiai átalakulások nem két különböző test között mennek végbe, hanem egy bizonyos rendszeren belül jelenlevő, de különböző kémiai természetű anyagok között történik átalakulás. E folyamatokhoz intenzív mennyiségek nem tartoznak, csak az intenzív mennyiségek különbségének megfelelő affinitás van meg. Minden egyes közelhatáshoz (fizikaihoz és kémiaihoz egyaránt) tartozik egy‑egy fajta affinitás és akkor van egyensúly, ha az affinitás nulla; nincs egyensúly, ha az affinitások eltérnek zérustól. A folyamatok mindig olyan irányban mennek végbe, hogy az affinitások zérus felé tartanak.
Az előzőkben már azt is említettük, hogy a közelhatásokkal kapcsolatos változások energiaátadással, energiaátalakulással járnak, mégpedig oly módon, hogy az a test, amelyben az intenzív mennyiség értéke nagyobb, energiát ad át annak, melyben az intenzív mennyiség értéke kisebb. Ha tehát két test különböző hőmérsékletű, akkor a nagyobb hőmérsékletű test felől fog energia áramlani a kisebb hőmérsékletű felé és így történik meg a kiegyenlítődés. Ha az egyik testben nagyobb a nyomás, mint a másikban, akkor a nagyobb nyomású test felől fog áramlani az energia a kisebb nyomású felé, s így létrejön a nyomás-kiegyenlítődés stb. A kölcsönhatások tehát energiaátadással járnak, az egyik rendszer energiájából a másik test energiája lesz és nem biztos, hogy ugyanolyan fajta energia, mint eredetileg volt. Az átadott energia mennyiségét egyszerűen ki tudjuk számítani, ha az intenzív mennyiségek különbsége igen kicsiny, de a testek energiája ugyanakkor viszonylag nagy. Ilyenkor ugyanis a folyamatosan leadott, ill. felvett energia alig változtatja meg az illető intenzív mennyiségek értékét. Könnyebb szemlélhetőség kedvéért gondoljunk megint a közlekedőedényekre. Tekintsünk két igen nagy kiterjedésű víztartályt, melyekben a vízszintkülönbség igen kicsiny. Ha egyikből a másikba engedünk pl. egy liter vizet, a szintkülönbség alig változik (észre sem vehető, valóban csak annyi, mint csepp a tengerben), az átadott vízmennyiség mégis jól lemérhető véges értékkel rendelkezik. Nos, hasonló feltételek a termodinamikai kölcsönhatások kapcsán is megvalósíthatók. Lényeges ismertetőjelük, hogy véges mennyiségű energiaátadás mellett, az intenzív mennyiségek észrevehetően nem változnak. Világos azonban, hogy még valaminek szintén észrevehető módon kell változnia ahhoz, hogy segítségével az energiacserét nagyság szerint jellemezhessük. Előre bocsátjuk, hogy ilyen jellemző mennyiség valóban minden kölcsönhatási típushoz tartozik. Pl. a nyomáskiegyenlítődéskor a térfogat változik meg. A megfelelő energiacsere (munkavégzés mértéke) ilyenkor a tapasztalás szerint a térfogatváltozással és a nyomással arányos. Pontosan: a nyomás $(p)$ és a térfogatváltozás $(\Delta V)$ szorzatának negatívja. Ugyanis az energiaveszteség a térfogat növekedésével, az energiafelvétel pedig térfogatcsökkenéssel jár; az energia- és a térfogatváltozás ellenkező előjelűek. Tehát a $p$ nyomáson történő $\Delta V$ térfogatváltozás
$$-p\cdot \Delta V$$
energiaváltozással jár. Teljesség kedvéért, e képlettel kapcsolatban, még egy körülményre kell felhívnunk a figyelmet. Az energia megmaradásának tétele szerint (feltéve, hogy csak ez az egyféle kölcsönhatás lép fel a két igen nagy kiterjedésű test között), az egyik test által leadott energia megegyezik a másik test által felvett energiával. Ha jól megfigyeltük az eddig mondottakat, akkor ezt a körülményt mennyiségileg is jellemezni tudjuk. Az egyik test nyomása $p+\Delta p$, a másiké $p$, ugyanakkor az egyik test térfogatváltozása nagyság szerint megegyezik a másikéval, de előjelük különbözik (ti. egyik test $\Delta V$-vel terjeszkedik a másik rovására, tehát a másik térfogata $\Delta V$-vel csökken). Nézzük most már az energiamérleget. A nagyobb $(p+\Delta p)$ nyomású test lead
$$-(p+\Delta p)\cdot \Delta V$$
energiát. Itt $\Delta V$ pozitív, hiszen az energiaveszteség - mint mondottuk - térfogatnövekedéssel jár. A másik test nyomása $p$, ez
$$-p\cdot \Delta V$$
energiát vesz fel. Az energia megmaradásának tétele szerint most már az kellene, hogy
$$(p+\Delta p)\Delta V=p\Delta V$$
$$p\Delta V+\Delta p \Delta V=p\Delta V$$
legyen, ez viszont nyilván nem állhat fenn. Innen az következne, hogy
$$\Delta p\cdot \Delta V=0$$
azaz, vagy a nyomáskülönbség $(\Delta p)$, vagy a térfogatváltozás $(\Delta V)$ egyenlő nullával, amikor viszont nincs folyamat. Ne ijedjünk meg, az ellentmondás nem elvi nehézségekből, csupán képletünk közelítő jellegéből származik. Ha $\Delta p\cdot \Delta V$ igen kicsiny $p\cdot \Delta V$‑hez képest, azaz $\Delta p$ igen kicsiny $p$‑hez képest, úgy a mérleg igen jó közelítéssel helyes.
Látjuk tehát, hogy a nyomás kiegyenlítődéssel járó energiaváltozás mértéke
$$-p\Delta V$$
csak közelítő érvényű. De azt is látjuk, hogy e közelítő jelleg annál jobb, minél kisebb a $\Delta p$ nyomáskülönbség a másik test $p$ nyomásához képest.
Érdekes módon, valamennyi kiegyenlítődési folyamat esetében hasonló formájú közelítő jellegű kifejezések érvényesek az energiaátadásra. Ha két igen nagy kiterjedésű elektromosan töltött test között igen kicsiny az elektrosztatikus potenciálkülönbség, úgy a folyamat közben átadott $\Delta e$ elektromos töltéssel együtt
$$\mathit{\Phi }\Delta e$$
nagyságú energia megy át egyik testből a másikba. $\mathit{\Phi }$ a "majdnem megegyező" elektrosztatikus potenciál. A $\Delta \mathit{\Phi }\cdot \Delta e$ ui. itt is elhanyagolható $\mathit{\Phi} \Delta e$ mellett, azaz $\Delta \mathit{\Phi }$ potenciálkülönbség elhanyagolható $\mathit{\Phi }$ potenciál értéke mellett. Tekintsünk most két egymással érintkező különböző fázisú (pl. az egyik folyadék a másik gőzállapotú) testet. Ha az egyes testek $K$‑számú kémiai anyag keverékéből állnak, melyek tömege az egyik testben $m_1,\ m_2, ...m_k$, a másikban $m_1,\ m_2, ...m_k$, úgy minden egyes kémiai anyag (kémiai komponens) külön‑külön, egymástól függetlenül átmehet a másikba. Tehát mindegyik kémiai komponens jelenléte külön‑külön anyagi kölcsönhatás lehetőségét eredményezi. Az egyensúly szükséges és elegendő feltétele az, hogy a megfelelő anyagok kémiai potenciáljai $(\mu )$ mindkét testben egyenlőek legyenek
$$\mu_1=\overline{\mu}_1$$
$$\mu_2=\overline{\mu}_2$$
$$. \\ . \\ . $$
$$\mu_{k}=\overline{\mu}_{k}$$
Pl. víz és alkohol keverékéből álló folyékony és légnemű fázisok közti egyensúlyhoz az szükséges, hogy külön mind a víz, mind az alkohol kémiai potenciálja megegyezzék mind a folyékony, mind a légnemű fázisban. Ha a folyékony állapotú testben a víz kémiai potenciálja nagyobb, mint a gőzállapotúban, de az alkoholra nézve nincs eltérés, úgy csak a víz fog párologni (csak a víz egy része megy át a folyékony állapotú testből a légneműbe). A párolgás addig tart, míg a víz kémiai potenciálja mindkét testben azonos értékű nem lesz. Mármost igen nagy kiterjedésű testek közötti igen kis kémiai potenciálkülönbség kiegyenlítődése
$$\mu_{i}\Delta m_{i}\ \ \ \ i=1,\ 2,\ ...,\ k$$
energiaátadással jár, ha az $i$‑edik kémiai komponens $m_1$ tömege $\Delta m_1$‑vel változik.
Az energiaátadással kapcsolatos fenti törvényszerűségek mindegyikében az illető közelhatásokhoz tartozó intenzív mennyiségek mellett egy‑egy új típusú mennyiség is jelentkezik. E mennyiségek számértéke mindig függ a test kiterjedésétől, tehát két testet egyesítve e mennyiségek értéke az egyesített rendszerre vonatkozóan mindig nagyobb lesz, mint külön‑külön az egyes részekre vonatkozóan. Pl. egy homogén nyomású test egyik felében uralkodó nyomás ugyanakkora mint az egész testé. Hasonlóképp hőmérséklete, elektrosztatikus potenciálja és kémiai potenciáljai is. Ellenben a test egy részének mind térfogata, mind töltése, mind a benne levő kémiai komponensek tömege kisebb, mint az egész test megfelelő adatai. Az ilyen, a kiterjedéstől függő mennyiségeket extenzív mennyiségeknek nevezzük.
Ha most áttekintjük az egyes kölcsönhatások törvényszerűségeit, rögtön szemünkbe tűnik, hogy valamennyi kölcsönhatáshoz tartozik nemcsak egy jellemző intenzív mennyiség, hanem egy jellemző extenzív mennyiség is. Egyelőre a hőhatáshoz tartozó extenzív mennyiséget ugyan nem ismerjük, de előrebocsájtjuk, hogy ez az entrópia. Sőt, az is igaz, hogy a kis hőmérsékletkülönbségek kiegyenlítődése közben a $\Delta S$ entrópiaváltozással együttjáró energiaváltozás $T$ hőmérsékleten:
$$T\cdot \Delta S$$
Az energiaátadásnak ezt a fajtáját hőközlésnek, az energiaváltozást hőnek nevezzük.
Még egy megjegyzést teszünk. Bármilyen kölcsönhatásra és a hozzátartozó $y$ intenzív és $x$ extenzív mennyiségre érvényes, hogy ha két nagy kiterjedésű test intenzív menynyisége $y$‑hoz képest csak kicsiny $\Delta y$‑al különbözik egymástól, akkor a $\Delta x$ extenzív mennyiséggel együtt szállított energia
$$y\cdot \Delta x$$
Az ilyen, igen kis kiegyenlítődéssel járó folyamatokat reverzibilis folyamatoknak szoktuk nevezni. Az elnevezés nem egészen találó, hiszen valójában ezek is kiegyenlítődési, a kiegyenlítődés irányába haladó, tehát egy irányú, azaz irreverzibilis folyamatok. De csak igen kismértékben irreverzibilisek, emiatt a fellépő energiaváltozások közelítő értékei igen egyszerű formában adhatók meg. Reverzibilis azaz megfordítható folyamat valójában tehát nincs. A reverzibilis elnevezés tényszerűen "alig irreverzibilis"‑t jelent.
Ha absztrakt jelöléssel az egyes kölcsönhatásokat rendre, $1.,\ 2.,\ ...i$‑edik, $...n$‑edik kölcsönhatásnak nevezzük és az $i$‑edikhez tartozó adatokat az $i$ indexszel látjuk el, úgy az $i$‑edik kölcsönhatáshoz tartozó reverzibilis energiaátadás
$$\Delta_iE=y_i\cdot \Delta x_i$$
| Kölcsön- hatás | Jellemző intenzív mennyiség | Jellemző extenzív mennyiség | "Reverzi- bilis" ener- giaválto- zás $\Delta E=$ | Exten- zív és in- tenzív mennyi- ség kap- csolata | |
| Mechani- kai | feszültség: $-p$ (nyo- más nega- tívja) | térfogat: $V$ | $-p\cdot \Delta V$ | $-p=\displaystyle \frac{\Delta E}{\Delta V}$ | |
| Elektro- sztatikus | elektroszta- tikus po- tenciál: $\mathit{\Phi}$ | elektromos töltés: $e$ | $\mathit{\Phi}\cdot \Delta e$ | $\mathit{\Phi}=\displaystyle \frac{\Delta E}{\Delta e}$ | |
| Termikus | hőmérsék- let: $T$ | entrópia: $S$ | $T\cdot \Delta S$ | $T=\displaystyle \frac{\Delta E}{\Delta S}$ | |
| Anyagi, minden ké- miai kom- ponensre kü- lön-külön | $1$ | 1. Kémiai kompo- nens po- tenciálja: $\mu_1$ | 1. kémiai kompo- nens töme- ge: $m_2$ | $\mu_1\cdot \Delta m_1$ | $\mu_1=\displaystyle \frac{\Delta E}{\Delta m_1}$ |
| $2$ | 2. Kémiai kompo- nens po- tenciálja: $\mu_2$ | 2. kémiai kompo- nens töme- ge: $m_k$ | $\mu_2\cdot \Delta m_2$ | $\mu_2=\displaystyle \frac{\Delta E}{\Delta m_2}$ | |
| $\cdot$ $\cdot$ $\cdot$ | $\ $ $\cdot $ $\cdot $ $\cdot $ | $\ $ $\cdot $ $\cdot $ $\cdot $ | $\ $ $\cdot $ $\cdot $ $\cdot $ | $\ $ $\cdot $ $\cdot $ $\cdot $ | |
| $k$ | $k$ Kémiai kompo- nens po- tenciálja: $\mu_k$ | $k$ kémiai kompo- nens töme- ge: $m_k$ | $\mu_k\cdot \Delta m_k$ | $\mu_k=\displaystyle \frac{\Delta E}{\Delta m_k}$ | |
| Általában | $y$ | $x$ | $y\cdot \Delta x$ | $y=\displaystyle \frac{\Delta E}{\Delta x}$ | |
Megengedve egyszerre, valamennyi kölcsönhatás fellépését az összes energiaváltozás:
$$\Delta E=\Delta_1 E+\Delta_2 E+\thinspace ...+\Delta_i E+\thinspace ...+\Delta_n E=\sum\limits_{i=1}^{n}\Delta_i E$$
$$\Delta E=\sum\limits_{i=1}^{n}y_i\cdot \Delta x_i$$
2. Az entrópia hőelméleti értelmezése
Tudjuk, hogy $p$ nyomáson a $\Delta V$ térfogatváltozással járó elemi térfogatmunka
$$\Delta W=-p\cdot \Delta V,\ \ p\neq 0\tag{1} \label{eq:(P)}$$
Ez összefüggés közvetlen felírására és jelentének megértésére az ad lehetőséget, hogy mind a munka, mind a nyomás, mind pedig a térfogat fogalmát külön‑külön jól ismerjük. Bizonyára nehezebben értenénk meg, ha $\Delta V$‑ről nem tudnánk, hogy micsoda, és éppen ennek az összefüggésnek a közvetítésével akarnánk erre fényt deríteni, sőt innen akarnánk a térfogat lényegét is megismerni. Míg itt a nehézség csak elképzelt, a hővel és az entrópiával kapcsolatban ez a valóságos helyzet. A $\Delta W$ elemi munka és a $\Delta Q$ elemi hőmennyiség, egyaránt az energia átalakulásait jellemző mennyiségek, azonban sem a munka $(W)$, sem a hőmennyiség $(Q)$ nem állapothatározók: értékük lényegesen függ a munkavégzés, ill. a hőhatás módjától. E hiányosságért mégis némileg kárpótol az $\eqref{eq:(P)}$ összefüggés, mely szerint a folyamatnak minden olyan elemi szakaszán, ahol munkavégzés nem történt, azaz $\Delta W=0$, szükségszerűen $\Delta V=0$, vagyis a térfogat, $V$ sem változik. Az is közvetlenül leolvasható, hogy a megállapítás fordítva is érvényes, ti. ha a térfogat állandó, a térfogatváltozás $\Delta V=0$ voltából $\Delta W=0$ következik. Ha pedig akár $\Delta W$, akár $\Delta V$ különbözik zérustól, a másik is különbözni fog. Mondjuk ki a tanulságot: a térfogat a testeknek olyan tulajdonsága, mely akkor és csakis akkor változik, ha a testen munkavégzés történik. Gondoljuk mostmár el az előbb is említett esetet, ti. azt, hogy a térfogatról csupán ennyit tudunk. Összehasonlítva ezt az értelmezést a térfogatra vonatkozó ismereteinkkel, valóban szegényesnek találjuk. Persze, ha a $V$ értelmezésére csak a fenti $\eqref{eq:(P)}$ összefüggés állna rendelkezésre, úgy ennyivel is meg kellene elégednünk.
Felmerül a kérdés, hogy az előbbi esettel analóg módon, van‑e a testeknek olyan állapothatározója, amely a nem állapothatározó hőmennyiséggel olyan viszonyban van, mint a térfogat a munkával? Szerencsés körülmény, hogy a kérdésre igennel válaszolhatunk. Pontos fogalmazásban az előbb még arra a nem mellőzhető körülményre is rá kellett volna mutatni, hogy $\Delta W$ és $\Delta V$ előbbi viszonya csupán olyan testekre vonatkozóan áll fenn, amelyek "bárikusan homogének", azaz amelyekben a nyomás mindenütt azonos értékű. Nevezzük a hőmennyiség esetében térfogathoz analóg fogalmat entrópiának és jelöljük $S$‑sel, ekkor a két fogalomkör között a következő megfelelés áll fenn:
| munka: $W$ | feszültség (negatív nyomás): $-p$ | térfogat: $V$ |
| hő: $\ Q$ | hőmérséklet: $\ \ T$ | entrópia: $S$ |
A közölt táblázat egyelőre tisztán spekulatív alapon veti fel a lehetőségeket, de nem egészen alaptalanul. Láttuk ugyanis, hogy ahogyan a mechanikai hatáshoz tartozó intenzitásparaméter a feszültség, ugyanúgy a hőhatás intenzitásparamétere a hőmérséklet.
A felvetett spekulatív lehetőség végiggondolása illetve kipróbálása célszerűnek látszik. Fel kell tételeznünk, hogy az elemi hőmennyiség‑változásra, $\Delta Q$‑ra is fönnáll egy a fenti $\eqref{eq:(P)}$‑gyel analóg összefüggés, és meg kell vizsgálnunk, hogy a belőle levont következtetéseket a tapasztalás igazolja‑e? Előrebocsájtjuk, hogy az "ötlet" jónak fog bizonyulni, azonban eredményes kiaknázásához még további bonyodalmakat kell kiküszöbölni. Mindenekelőtt írjuk át a fenti összefüggést a következő formába:
$$\frac{\ \Delta W\ }{\! \! \! -p}=\Delta V,\ \ p\neq 0$$
Felírva $Q$‑ra az analóg kifejezést
$$\frac{\Delta Q}{T}=\Delta S,\ \ T\neq 0$$
A $\Delta Q=0$, azaz $S=$állandóhoz tartozó állapotok összességét adiabatának nevezzük. Matematikai értelmezéséből következik, hogy a különböző adiabaták nem metszhetik egymást.
Az entrópia tehát a testeknek olyan tulajdonsága, amelynek változása a hőhatás jellépését, állandó volta pedig a hőhatás hiányát jelenti. Tekintsünk egy képzeletbeli folyamatot, melyben a hőhatás által közölt energiát az idő függvényében a következő grafikon ábrázolja:
Ugyanekkor, a mondottak szerint az entrópia változása:
A hőközlés és az entrópiaváltozás e kapcsolata mégsem jelenti azt, hogy egymással egyenes arányban változnak, ti. a
$$\Delta S=\frac{1}{T}\cdot \Delta Q$$
kapcsolatban az $\displaystyle \frac{1}{T}$ arányossági tényező nem állandó: maga is változik, méghozzá a külső körülményektől függően, de a $\Delta Q$ elemi hőmennyiség‑változástól függetlenül. Ha ez nem így volna, úgy az entrópia lényegében a felvett hő mértéke lenne, valójában viszont entrópia és hőhatás közt nem ilyen egyszerű az összefüggés. A bonyolult kapcsolatot csak fokozatosan, a kérdés újabb és újabb oldalról való megvilágításával tudjuk feltárni.
Az energia megmaradásának tétele szerint, ha egy testtel $\Delta Q$ elemi hőt és $\Delta W$ elemi munkát közlünk, akkor belső energiája éppen a munka és a hő összegével változik. Jelöljük a belső energia változását $\Delta E$‑vel, akkor a mondottak szerint
$$\Delta E=\Delta Q+\Delta W$$
Megjegyezzük, hogy $\Delta Q$ ill. $\Delta W$ akkor pozitív, ha a test kapja az energiát, ill. a testen végeznek munkát; ennek megfelelően mindkét mennyiség akkor negatív, ha a test $\Delta Q$ hőt ad környezetének, ill. $\Delta W$ munkát végez környezetén. Pozitív előjel tehát "bevételnek", negatív pedig "kiadásnak" felel meg. Ilyen szempontból indokolt a fenti egyenlőséget energiamérleg‑egyenletnek nevezni. A szóban forgó egyenlőséget gyakran célszerű a $\Delta Q$ és a A $\Delta W$ konkrét alakjának felhasználásával felírni. Láttuk ugyanis, hogy a munka kifejezhető a feszültség (negatív nyomás) és a térfogatváltozás szorzataként
$$\Delta W=-p\cdot \Delta V$$
és teljesen hasonlóképpen, a hő kifejezhető a hőmérséklet és az entrópiaváltozás szorzataként
$$\Delta Q=T\cdot \Delta S$$
Helyettesítsük be ezeket a fenti mérlegegyenletbe, akkor a hőelmélet következő fontos összefüggéséhez jutunk:
$$\Delta E=T\Delta S-p\Delta V$$
A következőkben ennek a fontos összefüggésnek néhány alkalmazását is bemutatjuk. (Még egyszer megjegyezzük, hogy ezek az összefüggések csak akkor érvényesek kielégítő pontossággal, ha az entrópia és a térfogat változása $(\Delta S$ ill. $\Delta V)$ oly kicsiny, hogy közben a hőmérséklet és a nyomás $(T$ ill. $p)$ gyakorlatilag állandónak tekinthető.)
3. A kiegyenlítődési folyamatok és az entrópia változása
Ezideig két alapvető megállapítást tettünk:
I. A hőtani folyamatok ún. kiegyenlítődési folyamatok. A kiegyenlítődés közelebbről azt jelenti, hogy az érintkező testek különböző kölcsönhatási típusaihoz (mechanikai-, elektromos-, hő- stb. hatások) tartozó intenzitásparaméterek közös szint kialakítására törekszenek: olyan folyamatok játszódnak le a rendszerben, melyek a nyomás-, elektromos potenciál-, hőmérséklet- stb. különbségek megszüntetésére irányulnak.
II. Minden testnek van egy olyan tulajdonsága, amely a testen végbemenő folyamatok közben a folyamatnak csupán azon szakaszain változik, ahol hőhatás történik. Ezt a tulajdonságot hívjuk entrópiának.
A továbbiakban az I. és II. kapcsolatával kell foglalkoznunk. Mindjárt ki is mondjuk a kapcsolatot megállapító harmadik alapvető tételt:
III. A kiegyenlítődési folyamatok közben a folyamatban résztvevő testek összentrópiája növekszik.
Másként ez azt jelenti, hogy a kiegyenlítődésre való törekvés és az entrópianövekedés ugyanannak a természeti törvénynek két különböző nézőpontból való megnyilvánulása. Így most már az is érthetővé vált, hogy miért nevezhettük a kiegyenlítődésre való törekvés törvényét entrópiatételnek, még az entrópiafogalom értelmezését megelőzően.
Első pillanatra úgy tűnik, mintha ilyen körülmények között az entrópiával való foglalkozás fölösleges luxus lenne. Valóban: ha a kiegyenlítődés törvénye mindent elmond a jelenségről, miért kell egy újabb fogalom bevezetésével még másképp is elmondani ugyanazt? Rögtön látni fogjuk: az entrópiafogalom azért szükséges, mert módot ad a különböző kölcsönhatások által létrehozott kiegyenlítődések összehasonlítására.
Vegyük figyelembe a mindennapi életből jól ismert kiegyenlítődési folyamatokat. Vizet akarunk melegíteni, de nem áll közvetlenül rendelkezésünkre a víznél melegebb test, amellyel a vizet érintkezésbe hozva a hőmérséklet különbség kiegyenlítődése révén emelhetnénk a víz hőmérsékletét. Mindez nem akadálya a vízmelegítésnek, hiszen gáz, szén, ill. fa elégetésével, vagy elektromos árammal a tűzhelyet fel tudjuk melegíteni. A közismert jelenségen most egy pillanatra meg kell ütköznünk. Hogyan? Hát meleget nemcsak melegebb testről, hanem kémiai átalakulásból is (égés) és elektromos áramból is nyerhetünk? Az igenlő válasz nem kétséges és nem is a tények azok, amelyeknek nem akarunk hinni. A kiegyenlítődés törvényének helyességében kell kételkednünk. Eredetileg a tűzhely és a környezet közös hőmérsékletű volt, de az égés, ill. elektromos áram hatására először a két "test" (tűzhely és környezet) hőmérséklete eltávolodott egymástól. Az eltávolodás azonban éppen ellenkezője a kiegyenlítődésnek. A látszólagos ellentmondás rögtön feloldódik, mihelyt figyelembe vesszük, hogy az égés és az elektromosság áramlása maga is kiegyenlítődési folyamat. Így végső okként itt is a kiegyenlítődés szerepel.
A különböző kiegyenlítődési folyamatok eme kapcsolatának áttekintésére foglalkozzunk a következő sematikus esettel: Legyen az $A$ és $B$ test (pl. $A$ a víz, $B$ a tűzhely) eredetileg közös hőmérsékletű. Mármost, ha csak a hőmérséklet kiegyenlítődésének folyamatát ismernénk, úgy az $A$ és $B$ közös hőmérsékletének egymástól való eltávolítását csak egy harmadik $C$ test segítségével tudnánk megvalósítani. Ha $C$ melegebb, mint $A$ és $B$, akkor pl. $B$ és $C$ kölcsönhatása révén $B$‑t fölmelegíthetnénk (természetesen $C$ hőmérsékletének csökkenése árán), vagyis $A$ és $B$ hőmérséklete eltávolodna egymástól. Mivel azonban másfajta kiegyenlítődési folyamatokat is ismerünk, alkalmas módon ezeket is igénybevehetjük a hőmérsékletkülönbség létrehozására. Egészen természetes módon merül fel a kérdés: adott körülmények közt milyen elektromos potenciálkülönbség (vagy más intenzitásmennyiségben fennálló különbség) kiegyenlítésének segítségével tudjuk létrehozni a kívánt hőmérsékletkülönbséget? Úgy érezzük, a különböző fajtájú és mennyiségű kiegyenlítődéseknek kell valamilyen közösen használható mértékkel rendelkezniük. Valóban, van ilyen mérték: az entrópia, ami tehát a kiegyenlítődési folyamatok világában ugyanazt a szerepet tölti be, mint az áruforgalomban a pénz. Ha az emberek csak egyféle áruval kereskednének, úgy a különböző mennyiségű áruk értékének összehasonlítása nem volna problematikus. $2\ \mathrm{q}$ búza kétszer annyit ér, mint $1\ \mathrm{q}$. De már pl. a búza értékének a kukorica, vagy különösen valamilyen szellemi munka értékével való összehasonlítása már bonyolultabb. Mind e nehézségeket az egyes áruk pénzértékének meghatározásával hidaljuk át. Teljesen hasonló a helyzet a kiegyenlítődési folyamatoknál. Különböző mennyiségű hőmérséklet‑kiegyenlítődések még könnyen összevethetők, de pl. hőmérsékletkülönbség‑kiegyenlítődésnek a nyomáskülönbség- ill. elektromos potenciálkülönbség‑kiegyenlítődéssel való összevetése már csak az entrópia segítségével folytatható le. Mégpedig azáltal, hogy mindenfajta kiegyenlítődési folyamatnak megvan a maga entrópiaértéke.
Még egy fontos körülményre kell felhívnunk a figyelmet. Az adás‑vételnél egyenlő értékű tárgyak cserélnek gazdát, így a résztvevő feleknél levő összérték változatlan marad. Így volna ez a hőelméletben is, ha nem lépne fel az adófizetésnek egy sajátos formája, amely egyébként minden adás‑vételnél felléphet. Ha egy házat többször eladnak és minden esetben lefizetik az adót, a házba befektetett összérték minden egyes tulajdonos‑változásnál növekszik. Ugyanez a helyzet minden kiegyenlítődési folyamatnál a folyamatban résztvevő testek összentrópiájával. A természetben csak ilyen folyamatok jöhetnek létre. Ha tehát meg akarjuk tudni, hogy bizonyos hőmérsékletkülönbséget létre lehet‑e hozni valamilyen adott elektromos potenciálkülönbség kiegyenlítésével, ki kell számítanunk a folyamattal járó entrópiaváltozást. Amennyiben a számítás azt mutatja, hogy az entrópia növekszik, úgy a kitűzött cél elérhető, ha azonban a számítás eredményéül entrópiacsökkenés adódna, úgy a folyamat nem valósítható meg.
Azt mondottuk, hogy minden fajta kiegyenlítődési folyamatnak megvan a maga entrópiaértéke. Mindez matematikailag is oly egyszerű, hogy érdemes részletesebben is foglalkozni a kérdéssel. Az előző pont végén megismerkedtünk az "energiamérleg" következő formájával
$$\Delta E=T\cdot \Delta S-p\cdot \Delta V$$
Az összefüggés ebben az alakban természetesen csak akkor érvényes, ha hőhatáson és mechanikai munkán (térfogatmunka) kívül más hatás nem lép fel. További hatások fellépése természetesen további energiaátadással jár, melyeket az energiamérlegben is figyelembe kell vennünk. Nekünk azonban most nem feladatunk, hogy olvasóinkat a legáltalánosabban adódó esetek végigszámolásával megismertessük, ezért megmaradunk csupán kétféle kölcsönhatás figyelembevétele mellett. A mérleg‑egyenlet egyszerű átrendezésével és $T$‑vel való végigosztással a következő kifejezést kapjuk az entrópiaváltozásra:
$$\Delta S=\frac{1}{T}\Delta E+\frac{p}{T}\Delta V$$
Figyeljük meg jól: ebben a formájában fenti egyenletünk entrópiamérlegnek tekinthető, ahol
$$\frac{1}{T}\cdot \Delta E$$
az entrópiaváltozásnak az a része, mely a rendszer energiaváltozása folytán lép fel és
$$\frac{p}{T}\cdot \Delta V$$
az entrópiaváltozás térfogatváltozásra eső része.
A nyert összefüggések megvilágításában vizsgáljuk meg néhány kiegyenlítődési folyamat entrópiamérlegét. Azt fogjuk találni, hogy az entrópia minden kiegyenlítődési folyamat esetében növekszik. Tekintsünk evégből egy csupán két homogén testből álló, zárt rendszert. Az egyik test adatai (térfogata, belső energiája, nyomása, hőmérséklete) legyenek: $V_1,$ $E_1,$ $p_1,$ $T_1;$ a másiké: $V_2,$ $E_2,$ $p_2,$ $T_2$. Az a körülmény, hogy a két testből álló rendszer zárt, abban jut kifejezésre, hogy együttes energiájuk és együttes térfogatuk a kiegyenlítődés közben változatlan marad. Tehát: az együttes térfogat
$$V=V_1+V_2$$
és az együttes energia
$$E=E_1+E_2$$
külön‑külön állandó. Ugyanez az összefüggés átírható a kiegyenlítődési folyamattal járó változásokra is, mivel pedig a rendszer össztérfogata az össz belsőenergiája állandó, ezek változása zérus, azaz:
$$\Delta V=0,\ \ \ \Delta E=0$$
tehát
$$\Delta V_1+\Delta V_2=0$$
továbbá
$$\Delta E_1+\Delta E_2=0$$
Az utóbbi két összefüggés jelentése igen egyszerű: amennyivel nő (ill. csökken) az egyik test térfogata, annyival csökken (ill. nő) a másiké. Hasonlóképp: amennyi energiát veszít (ill. nyer) az egyik test, annyit nyer (ill. veszít) a másik. Ezt a körülményt kiemelve, a rendszer "zárt"‑ságát a következőképp is jellemezhetjük: egyrészt
$$\Delta V_1=-\Delta V_2$$
másrészt
$$\Delta E_1=-\Delta E_2$$
Írjuk fel mostmár az entrópiamérleget külön‑külön mindkét testre vonatkozóan
$$\Delta S_1=\frac{1}{T_1}\Delta E_1+\frac{p_1}{T_1}\Delta V_1$$
$$\Delta S_2=\frac{1}{T_2}\Delta E_2+\frac{p_2}{T_2}\Delta V_2$$
Vegyük továbbá figyelembe a "zárt"‑ságból adódó kikötéseket, így a második test entrópiamérlege előállítható az első test térfogatváltozásának és energiaváltozásának segítségével:
$$\Delta S_2=-\frac{1}{T_2}\cdot \Delta E_1-\frac{p_2}{T_2}\cdot \Delta V_1$$
Már csak az van hátra, hogy mostmár — az egyes testek entrópiamérlegének ismeretében — az egész zárt rendszer entrópiamérlegét is felírjuk. Másként ez azt jelenti, hogy fel kell írnunk a $\Delta S_1+\Delta S_2$ entrópiaösszeget, ami a teljes rendszer entrópiájának megváltozása. Elvégezve az összeadást, a megfelelő tagok összevonása után kapjuk a rendszer össz‑entrópiaváltozására:
$$\Delta S=\left(\frac{1}{T_1}-\frac{1}{T_2}\right)\cdot \Delta E_1+\left(\frac{p_1}{T_1}-\frac{p_2}{T_2}\right)\Delta V_1$$
Vegyük még azt is figyelembe, hogy $T_1,$ $T_2,$ $p_1,$ $p_2$ mindegyike pozitív (abszolút skála).
Ezután rátérhetünk a hőmérséklet- és nyomáskiegyenlítődés folyamatának közelebbi vizsgálatára. Foglalkozzunk először a hőmérsékletkiegyenlítődéssel. Legyen az $1$‑es jelzésű test a magasabb hőmérsékletű. Ez annyit jelent, hogy $T_1$ nagyobb $T_2$‑nél:
$$T_1>T_2>0$$
A testekben uralkodó nyomás pedig legyen egyenlő
$$p_1=p_2=p>0$$
(Utóbbi azt jelenti, hogy csak hőmérsékletkiegyenlítődést vizsgálunk.) Ilyen módon az entrópiaváltozás
$$\Delta S=\left(\frac{1}{T_1}-\frac{1}{T_2}\right)\cdot \Delta E_1+\left(\frac{1}{T_1}-\frac{1}{T_2}\right)p\cdot \Delta V_1$$
$$\Delta S=\left(\frac{1}{T_1}-\frac{1}{T_2}\right)(\Delta E_1+p\Delta V_1)$$
Azt kell megvizsgálnunk, hogy ez a kifejezés milyen előjelű. Mivel a mondottak szerint $T_1>T_2>0,$ azért az első tényező negatív. Ugyanis
$$\frac{1}{T_1}-\frac{1}{T_2}=\frac{T_2-T_1}{T_1T_2}<0$$
Hiszen
$$T_2-T_1>0$$
Vegyük észre, hogy a második tényező éppen az $1$‑es — tehát a magasabb hőmérsékletű test hőhatása
$$\Delta Q_1=\Delta E_1+p\cdot \Delta V_1$$
Mivel kiegyenlítődés közben a magasabb hőmérsékletű test ad át hőt az alacsonyabb hőmérsékletűnek, a $Q_1$‑nek megfelelő energiát az $1$‑es test leadja, vagyis $\Delta Q_1$ negatív:
$$\Delta Q_1<0$$
Látjuk, tehát, hogy $\Delta S$ két negatív előjelű kifejezés szorzata, vagyis az entrópiaváltozás pozitív:
$$\Delta S>0$$
Zárt rendszeren belül végbemenő hőmérsékletkiegyenlítődés közben az entrópia növekszik.
Másik példaként foglalkozzunk a nyomáskiegyenlítődéssel. Legyen tehát a két test egyenlő hőmérsékletű.
$$T_1=T_2=T>0$$
és az $1$‑es test $p_1$ nyomása nagyobb a másikénál
$$p_1>p_2>0$$
Az entrópiaváltozásra megállapított általános kifejezést alkalmazzuk erre a speciális esetre. A mondottak szerint
$$\Delta S=\left(\frac{1}{T}-\frac{1}{T}\right)\cdot \Delta E_1+\frac{p_1-p_2}{T}\cdot \Delta V_1$$
ahol a jobboldal első tagja nyilvánvalóan zérus és így
$$\Delta S=\frac{p_1-p_2}{T}\Delta V_1$$
A $\Delta V_1$ nyilvánvalóan pozitív, hiszen a nagyobb nyomású test azáltal végez munkát, hogy a kisebb nyomású testet kisebb térfogatúvá nyomja össze: a kisebb nyomású test térfogata csökken, a nagyobb nyomásúé növekszik. Mivel $p_1$ nagyobb $p_2$‑nél, $p_1-p_2$ szintén pozitív, amit az ugyancsak pozitív $T$‑vel osztva továbbra is pozitív számot kapunk.
$$\frac{p_1-p_2}{T}>0$$
Ennek és az ugyancsak pozitív A $\Delta V_1$‑nek szorzata az entrópiaváltozás, ami tehát szintén pozitív
$$\Delta S>0$$
A tárgyalt két példa kombinációjaként azzal az esettel is foglalkozhatnánk, amidőn a rendszeren belül a hőmérséklet- és nyomáskiegyenlítődés egyidejűleg megy végbe. Ez az eset azonban visszavezethető az előbb tárgyalt esetekre, úgy fogva fel a dolgot, mintha e folyamatban kis szakaszonként felváltva, követnék egymást egymás után a hőmérséklet- ill. nyomáskiegyenlítődési rész-szakaszok.
4. A Carnot-féle körfolyamat. A II. fajú perpetuum mobile lehetetlensége
Vizsgáljuk meg vázlatosan, hogyan működik egy hőerőgép? A gép egy $T_1$ hőmérsékletű ún. hőtartályból hőhatás formájában energiát von el, majd az energiát munkavégzés formájában továbbadja és egy alacsonyabb $T_2$ hőmérsékletű testnek hőt ad át. Ezután újból a $T_1$ hőmérsékletű tartállyal érintkezve ismét felmelegszik és az előbbi folyamat megismétlődik. A gép tehát újra és újra visszajut eredeti állapotába (körfolyamat) és közben a tartályból felvett hő rovására munkát végez.
Nézzük meg közelebbről a fenti körfolyamat esetében a mennyiségi viszonyokat. Ennek érdekében figyeljük meg az ún. Carnot‑féle körfolyamat minden állomását és minden szakaszát. Legegyszerűbb esetben négy állomást és az ezeket összekötő négy szakaszt különböztethetünk meg
Az 1. kezdeti állapotban a gép a $T_1$ hőmérsékletű tartállyal tart egyensúlyt, tehát maga is $T_1$ hőmérsékletű. Az 1. állapotból a 2. állapotba vezető I. folyamat közben továbbra is $T_1$‑el áll kapcsolatban és $Q_1$ hőcsere történik köztük. ($Q_1$ pozitív, ha a gép kapja, és negatív, ha a gép leadja ezt a hőmennyiséget. Az általánosság kedvéért most mindkét lehetőséget meg kell engednünk.) A 2.‑ből 3.‑ba vezető II. folyamat közben a gép nincs kapcsolatban egyik tartállyal sem, csupán munkát végez. (A munka pozitív, ha a gép a környezetnek lead energiát, és negatív, ha a környezetből kap közben energiát. Utóbbi esetben negatív munkavégzésről beszélünk.) Ugyanekkor a gép hőmérséklete $T_1$‑ről $T_2$‑re hűl le. A III. lépésben (3.‑ból 4.‑be) a gép a $T_2$‑vel áll kapcsolatban és $Q_2$ nagyságú hőcsere jön köztük létre. (A $Q_2$ hőmennyiséget megint csak akkor számítjuk pozitívnak, ha a gép kapja az energiát, vagyis, ha a tartály leadja.) Végül IV. lépésben (4.‑ből 1.‑be) tisztán munkavégzéssel visszajut a gép eredeti állapotába, miközben előbbi $T_2$ hőmérséklete ismét $T_1$‑re emelkedik. Ezzel az első kör bezárult és kezdődhet a következő. Most már csak az adatokat tekintve, vizsgáljuk meg még egyszer a körfolyamat egyes szakaszait:
I. szakasz: a gép a $T_1$ hőmérsékletű tartállyal kapcsolva $T_1$ hőmérsékleten $Q_1$ nagyságú hőcserét végez.
II. szakasz: a gép hőmérséklete $T_1$‑ről $T_2$‑re csökken. Csak munkavégzés van, hőmennyiséget a gép nem vesz fel és nem ad le.
III. szakasz: a gép a $T_2$ hőmérsékletű tartállyal kapcsolva $T_2$ hőmérsékleten $Q_2$ nagyságú hőcserét végez.
IV. szakasz: a gép hőmérséklete $T_2$‑ről $T_1$‑re emelkedik. Éppúgy, mint a II. szakaszban, most is csak munkavégzés van, hőmennyiséget a gép nem vesz fel és nem ad le.
Jegyezzük meg jól: $T_1$ a nagyobb és $T_2$ a kisebb hőmérsékletet jelenti, valamint azt is, hogy a $T$ hőmérsékletet abszolút skálában mérjük, így értéke mindig pozitív. ($T=0$ és $T$ negatív már nem lehet.) Azt is vegyük még egyszer figyelembe, hogy a $Q_1$ hőmennyiség pozitív, ha a gép felveszi és negatív akkor, ha a gép leadja a hőenergiát. Hasonlóképpen állapítjuk meg a $Q_2$ hőmennyiség előjelét. Végül, tudjuk, hogy a körfolyamat végén a gép energiája annyi, mint eredetileg volt, mivel újra eredeti állapotában van. Jelöljük a teljes körfolyamat során végzett munkát $W$‑vel; az energia megmaradásának tétele szerint a $W$ munkavégzés csakis az I. és III. szakaszbeli hőből származhatik, azaz
$$Q_1+Q_2=W\tag{1} \label{eq:(15243)}$$
(Mint mondottuk $W$ pozitív, ha a gép végez kifelé munkát és negatív, ha a gép működése a környezetből való energia elvonással jár.) Ez az egyenlet az ún. energiamérleg. Nézzük meg az entrópiamérleget is. Az entrópiaváltozás a $Q_1$ hőcsere folytán
$$\frac{Q_1}{T_1}$$
és a $Q_2$ hőcsere folytán
$$\frac{Q_2}{T_2}$$
Az összes entrópiaváltozás ezekből és a még ezen felül köteles $\Delta S$ irreverzibilis entrópianövekedésből adódik ki. $(\Delta S>0.)$ Mivel azonban a körfolyamat végén a gép ismét eredeti állapotában van, entrópiája is annyi, mint eredetileg, vagyis a gép entrópiájának összes változása zérus:
$$\frac{Q_1}{T_1}+\frac{Q_2}{T_2}+\Delta S=0$$
(vigyázzunk: ez a mérleg csak a gépre vonatkozik. A gép, a tartályok és a munkát felvevő környezet összes entrópiája feltétlenül növekszik. Maga a gép viszont ismét eredeti állapotában van, így entrópiája is az eredeti értéket veszi fel.) Mivel az entrópianövekedés tétele szerint
$$\Delta S>0$$
azért a fenti mérleg így is írható:
$$\frac{Q_1}{T_1}+\frac{Q_2}{T_2}<0\tag{2} \label{eq:(6978)}$$
Az $\eqref{eq:(15243)}$ összefüggés energiamérlegből és a $\eqref{eq:(6978)}$ összefüggés entrópiamérlegből fontos következtetéseket vonhatunk le. Mindenekelőtt bebizonyítjuk, hogy nem lehetséges ún. II. fajú perpetuum mobile.
II. fajú perpetuum mobilének nevezhetnénk egy olyan gépet, amely egyetlen hőtartályból hőt vonna el, és ezt teljes egészében munkavégzésre használná. Igaz, hegy az ilyen gép az energiatétel szerint működne, tehát a munkát nem a semmiből, hanem hőhatás formájában nyert energiából végezné; bizonyos értelemben mégis örökmozgó lenne ez a szerkezet, mert hőtartály mindig és mindenütt rendelkezésünkre áll. A tenger vize pl. annál több energiát tartalmaz, minél nagyobb a hőmérséklete; s mivel víztömege igen nagy, még alacsony hőmérsékleten is mérhetetlen sok energia van elraktározva benne. Gondoljunk olyan hajóra, melynek motorja a tenger vizéből vonja el a hajtáshoz szükséges energiát. A felvett energia meghajtja a gépet, mozgásba hozza a hajót és a súrlódás folytán visszaszármazik a tengerbe. Látjuk, hogy a hajó mozgatásához ebben az esetben nem kellene külön üzemanyag, így végeredményben szerkezetünk örökmozgó lenne. Tapasztalatból jól tudjuk, hogy ilyen gép nem működik; de a fizikában járatlan emberek gyakran még ma is megpróbálkoznak II. fajú perpetuum mobile készítésével, természetesen mindannyiszor eredménytelenül.
A fentiekben megismert $\eqref{eq:(15243)}$ és $\eqref{eq:(6978)}$ egyenletek alapján már be lehet látni, hogy a II. fajú perpetuum mobile, azaz a csupán egyetlen hőtartályból működő gép lehetetlenség. Ugyanis, ha csak egyetlen tartály áll rendelkezésünkre, úgy a Carnot‑féle körfolyamat III. lépésben ismét a $T_1$ hőmérsékletű tartállyal kell a gépet kapcsolni, azaz $T_1=T_2$. Ennek megfelelően a $\eqref{eq:(6978)}$ egyenlőtlenséget így kell írnunk:
$$\frac{Q_1}{T_1}+\frac{Q_2}{T_1}<0$$
Szorozzuk át ezt az egyenlőtlenséget $T_1$‑el, úgy a
$$Q_1+Q_2<0$$
egyenlőtlenséghez jutunk. Vegyük továbbá figyelembe, hogy $\eqref{eq:(15243)}$ szerint
$$Q_1+Q_2=W$$
A kifelé termelt munka tehát negatívnak adódik $(W<0)$, vagyis a gép nem képes pozitív munkát végezni. Sőt, az egész szerkezet csak úgy működhet, ha magán a gépen végzünk munkát. Ami egyúttal azt jelenti, hogy a II. fajú perpetuum mobile nem lehetséges.
Fentiekből láttuk, miképpen nem működhet a gép; most nézzük meg miképpen működhet. Vegyük először szemügyre a $\eqref{eq:(6978)}$ egyenlőtlenséget. Eszerint $\displaystyle \frac{Q_1}{T_1}$ és $\displaystyle \frac{Q_2}{T_2}$ összege negatív, ami nyilván csak úgy lehetséges, ha a két összeadandó közül legalább az egyik negatív. Mivel pedig $T_1$ és $T_2$ hőmérsékletek pozitívak, a $Q_1$ és $Q_2$ hőmennyiségek közül kell vagy egyiknek, vagy mindkettőnek negatívnak lennie. A továbbiakban részben ez, részben az a következő megállapítás szolgál alapul, hogy az $W$ munka csak akkor lehet pozitív, ha $Q_1$ (a magasabb hőmérsékletű tartályból elvont hő) szintén pozitív. Ha pedig $Q_1$ negatív, úgy $W$ is az. Ez utóbbi állításunkat azonban még be kell bizonyítanunk.
Megint csak a $\eqref{eq:(6978)}$ egyenlőtlenségből indulunk ki, amely szerint
$$\frac{Q_1}{T_1}+\frac{Q_2}{Q_2}<0$$
Az egyenlőtlenség nem változik, ha egyidejűleg $\displaystyle \frac{Q_1}{T_2}$‑t hozzáadunk és ugyancsak $\displaystyle \frac{Q_1}{T_2}$‑t le is vonunk
$$\frac{Q_1}{T_1}-\frac{Q_1}{T_2}+\frac{Q_2}{T_2}+\frac{Q_1}{T_2}<0$$
Ha az első két tagból a $Q_1$‑et, a második kettőből az $\displaystyle \frac{1}{T_2}$‑t kiemeljük, az egyenlőtlenséget így rendezhetjük át:
$$Q_1\left(\frac{1}{T_1}-\frac{1}{T_2}\right)+\frac{Q_1+Q_2}{T_2}<0$$
Mivel $\eqref{eq:(15243)}$ összefüggésünk szerint $Q_1+Q_2$ helyett $W$ írható, - egyszerű számolással belátható - :
$$\frac{1}{T_1}-\frac{1}{T_2}=\frac{T_2-T_1}{T_1T_2}-\frac{\eta }{T_2}$$
$\eta$‑val jelöltük a következő pozitív előjelű kifejezést
$$\eta =\frac{T_1-T_2}{T_1}>0$$
ez mindig pozitív, mivel $T_1$ mindig nagyobb $T_2$‑nél a fenti egyenlőtlenség így írható:
$$-Q_1\frac{\eta }{T_2}+\frac{W}{T_2}<0$$
Ezt végigszorozva a pozitív $T_2$‑vel, és a negatív előjelű tagot ellentétes előjellel a másik oldalra téve, a következő alapvető összefüggést nyerjük:
$$\boxed{W<\eta Q_1}$$
Ezek szerint $W$ kisebb $\eta\cdot Q_1$‑nél és mivel $\eta $ pozitív, ha $Q_1$ negatív, úgy $\eta \cdot Q_1$ is negatív, tehát a nála kisebb $W$‑nek is negatívnak kell lennie. Másrészt, ha $W$ pozitív, a nála nagyobb $\eta\cdot Q_1$‑nek is pozitívnak, azaz $Q_1$‑nek is pozitívnak kell lennie. A mondottak szerint ha $Q_1$ (a $T_1$ hőmérsékletű tartály esetében fellépő hőhatás) negatív, akkor a gép által végzett munka is negatív (azaz a környezet végez munkát a gépen); illetve a gép által végzett munka csak úgy lehet pozitív, ha $Q_1$ is az (ami annyit jelent, hogy gépünk hőt von el a $T_1$ hőmérsékletű tartályból). Milyen módon lehet tehát pozitív munkavégzést nyernünk gépünktől? Iménti tételünk szerint, ha $W$ pozitív, úgy szükségszerűen $Q_1$ (a nagyobb hőmérsékletű tartályból nyert hő) is pozitív:
$$Q_1>0$$
Az előző tétel azt mondja ki, hogy $Q_1$ és $Q_2$ közül legalább az egyik negatív. Láttuk, hogy $Q_1$ pozitív, így $Q_2$‑nek feltétlenül negatívnak kell lennie. Ezzel következtetéssorozatunk végére jutottunk, csupán össze kell foglalni a tanulságot:
Körfolyamattal csak úgy nyerhetünk pozitív munkát, ha két különböző hőmérsékletű hőtartály áll rendelkezésre. Ezek közül a nagyobb hőmérsékletű tartályból a gép $Q_1$ hőt vesz fel, ennek egy részét munkává alakítja, majd a maradék $Q_2$ mennyiségű hőt átadja az alacsonyabb hőmérsékletű tartálynak.
Ez a következtetés teljes mértékben összhangban áll a II. fajú perpetuum mobile lehetetlenségével, de annál többet is mond: a gép a felvett hőt nem képes teljes egészében munkává alakítani, hanem egy részét továbbadja egy alacsonyabb hőmérsékletű tartálynak. Ha ilyen alacsonyabb hőmérsékletű tartály nem áll rendelkezésre, munkát sem nyerhetünk. A gőzmozdony esetében például a magasabb $T_1$ hőmérsékletű tartálynak a felmelegített gőz felel meg, a kisebbik $T_2$ hőmérsékletű tartály maga a környezet. Amennyiben tehát a mozdony olyan meleg környezetbe futna be, melynek hőmérséklete megegyezne a gőztér hőmérsékletével, a gép és a mozdony leállna.
A fentiekben megismert (bekeretezett) egyenlőtlenség szerint
$$W<\eta \cdot Q_1$$
Átosztva a pozitív $Q_1$‑el
$$\frac{W}{Q_1}<\eta =\frac{T_1-T_2}{T_1}<1$$
Az egyenlőtlenség baloldalán szereplő
$$\frac{W}{Q_1}$$
hányados az ún. hatásfok. Megmutatja ugyanis, hogy a gép által felvett hőnek hányad része hasznosítható. Mivel $\eta $ mindig kisebb $1$‑nél, világosan látszik, hogy a felvett hőnek csak bizonyos tört része alakítható munkává. Az $\eta $ éppen azt a felső határt jelenti a hatásfokban, amelyik már sohasem érhető el:
$$\frac{W}{Q_1}< \frac{T_1-T_2}{T_1}$$
Max Planck, a kvantumelmélet megalapítója, hőelmélettel is sokat foglalkozott. Egyik hőelméleti könyvében említi, hogy érdekes, akár meleget, akár hideget akarunk előállítani, annak mindenképp ára van. Pontosabban megfogalmazva ez azt jelenti, hogy alacsonyabb hőmérsékletű tartályból csak úgy vihetünk át hőt a magasabb hőmérsékletűre, ha ennek érdekében munkát fektetünk be. Valóban, az a körülmény, hogy alacsonyabb hőmérsékletű tartályból hőt vonunk el, előbbi terminológiánk szerint azt jelenti, hogy $Q_2$ pozitív és $Q_1$ negatív: ha viszont $Q_1<0$, úgy - iménti tételünk szerint - $W$ is negatív, vagyis kívülről kell munkát befektetni és csakis e külső munkabefektetés rovására lehet az alacsonyabb hőmérsékletű tartályból a magasabb hőmérsékletűbe hőt átvinni. Ez egyébként a hűtés folyamata, mely éppen abból áll, hogy a hidegebb testről állandóan hőt vonunk el. Így hűteni viszont csak munkavégzés árán lehet. (Eltekintve attól a nyilvánvaló esettől, midőn egy harmadik, még hidegebb testet veszünk igénybe.)
5. Clausius az entrópiatételről
Az entrópiatétel sokféle formában kifejezhető. R. Clausius egyik népszerűsítő előadásában igyekezett olyan megfogalmazást adni, amely nem szakemberek számára is viszonylag könnyen hozzáférhető. Ebben a tárgyalásmódban Clausius egy azóta feledésbe ment - lényegében az entrópiával azonos jelentésű - fogalmat, a diszgregáció fogalmát használja.
Az alábbiakban szemelvényesen ismertetjük Clausius gondolatmenetét az említett népszerűsítő előadás$^{10}$ alapján:
"A második tétel kevésbé ísmeretes, mint az első és különösen a mechanikai hőelmélet népszerű fejtegetéseiben néha teljes hallgatással mellőzik. Ennek elsősorban az az oka, hogy sokkal nehezebben érthető, mint az első: tárgyalásánál olyan fogalmak kerülnek szóba, amelyeket csak ez alkalommal vezetünk be; továbbá olyan fogalmakat kell egymással összehasonlítani, amelyeket eddig nem tekintettek mechanikai mennyiségeknek. Mihelyt hozzászoktunk azonban az itt szükséges tárgyalási módhoz, a második főtétel éppen olyan egyszerűnek és természetesnek tűnik majd, mint az első.
Megpróbálom úgy megvilágítani az itt szóban forgó folyamatokat, hogy az összehasonlítás új módja magától mutatkozzék szükségesnek. Ezáltal az első mellett a második főtétel jogosultsága is világosan előtérbe lép.
Ha megvizsgáljuk, hogy milyen körülmények között alakul át a hő munkává és fordítva, a munka hővé, elsőként a következő folyamat tűnik szemünkbe: a testekben felhalmozott hőnek az a törekvése, hogy megváltoztassa a testek állapotát. A hő kitágítja a testeket, szilárd halmazállapotból cseppfolyós és légnemű halmazállapotba viszi át azokat és hozzátehetjük, a kémiai vegyületeket igyekszik elemeire bontani. Mindezen esetekben a hő hatása abban áll, hogy a molekulák és az atomok közt levő kapcsolatot lazítja vagy teljesen felbontja, és azokat a molekulákat, amelyek már semmiféle kapcsolatban nincsenek egymással, lehetőleg messzire eltávolítja egymástól.
Mindennek rövid kifejezésére egy mennyiséget vezettem be, amely megadja, hogy egy testnél mennyire ment végbe a legkisebb részecskék hőokozta szétválása és eltávolodása. Ezt a mennyiséget a test diszgregációjának (szétválásának) neveztem el. Valamely test diszgregációja a három halmazállapot közül a szilárd állapotban a legkisebb, a folyékonyban nagyobb, a légneműben a legnagyobb. Az utóbbi állapotban még azáltal nőhet meg, hogy a molekulák még jobban távolodnak egymástól, vagyis a gáz tovább kitágul. Éppen így általában a diszgregáció növekedésével jár a kémiailag összetett testnek elemeire való szétbomlása is.
Ezen fogalom segítségével á hő hatását így fejezhetjük ki: a hő növelni igyekszik a test diszgregációját.
Hogy azonban egy test diszgregációját növeljük, rendszerint ellenállásokat kell legyőznünk, éspedig kétféle ellenállást. Először, hogy a molekulák összetartását egészben vagy részben megszüntessük, azokat az erőket kell legyőznünk, amelyekkel a molekulák egymást vonzzák; ezen belső erők mellett rendszerint le kell még győznünk idegen, a testre kívülről ható erőket is. Ha pl. egy külső nyomás alatt álló testnek ki kell tágulnia, úgy le kell győznie azt a nyomást is, amely a térfogat növekedésével szemben hat. A hőnek tehát a diszgregáció növelésével a vele szembeszegülő erők legyőzésével belső és külső munkát kell kifejtenie: a diszgregáció növekedésénél a hőnek munkává való alakulása megy végbe.
Fordítva, a diszgregáció csökkenéséhez munkát (éspedig általában külső és belső munkát) kell befektetni, hogy azok az erők, amelyeket előző esetben a hő győzött le, most maguk győzzék le a hőt. Ennél a folyamatnál hő keletkezik; eredményül tehát azt kapjuk, hogy diszgregáció‑csökkenésnél a munka hővé alakul át.
Bizonyos okból - amelyről később még szó lesz -, egyelőre tételezzük fel, hogy minden változás, amelyet szemügyre veszünk, oly módon történik, hogy a fordított változások is pontosan ugyanolyan körülmények között végbemehetnek. Ezeket a változásokat röviden megfordítható változásoknak fogjuk nevezni. Feltételezve ezeket a korlátozásokat, mondhatjuk, hogy diszgregáció‑növekedésnél ugyanannyi hő alakul át munkává, mint amennyi munka alakul hővé a megfelelő diszgregáció csökkenésnél.
A mondottakból látható, hogy egyrészt a diszgregáció‑változások között, másrészt a hőnek munkává, vagy fordítva történő alakulása között okozati összefüggés áll fenn, amelyet valamilyen módon határozott törvényszerűségként mondhatunk ki. Hogy ennek a törvénynek lehetőleg egyszerű alakot adjunk, meghatározott kifejezésmódot kell még bevezetnünk.
Eddig azt a folyamatot, amikor hő felhasználásával munka, vagy munka felhasználásával hő keletkezett, átváltozásnak neveztük, amennyiben azt mondottuk, hogy hő munkává, vagy munka hővé változik át. Éppen így nevezhetjük a diszgregáció‑változást is átalakulásnak. Ti. a test legkisebb részecskéi között eredetileg fennálló elrendeződés egy más elrendeződéssé alakul át.
E kétféle átalakulás mindegyike ellentétes módon történhet. Ezért pozitív és negatív kifejezésekkel különböztetjük meg őket egymástól. A diszgregáció növekedést pozitívnak, a diszgregáció csökkenést negatívnak tekintjük. Tekintsük továbbá a munkának hővé való átalakulását pozitívnak, a hőnek munkává való átalakulását pedig negatívnak.
Ha most visszatérünk az előbb vizsgált folyamatokhoz, látjuk, hogy valamely test diszgregáció növekedésénél (ami pozitív átalakulás) egyúttal hőnek munkává való átalakulása (azaz negatív átalakulás) is végbemegy és éppúgy a negatív diszgregációnál: a munkának hővé való pozitív átalakulása is lejátszódik. Ebből első eredményként tehát azt kapjuk, hogy mindkét esetben egyszerre egy pozitív és egy negatív átalakulás következik be.
Az átalakulásoknál azonban nemcsak az előjelet, hanem a nagyságot is figyelembe kell vennünk. Egy test diszgregációja nagyobb vagy kisebb mértékben változhatik meg, és hasonlóképp több, vagy kevesebb hő alakulhat át munkává vagy jöhet létre munkavégzés árán. Ha előzetesen már megállapítottuk a változások mérésének módját is, minden változás értékét meghatározott matematikai menynyiséggel fejezhetjük ki, amelyet az átalakulás egyenértékének fogunk nevezni.
Ezen egyenértékkel kapcsolatban fel kell most vetnünk a kérdést: meghatározható‑e oly módon, hogy egy test megfordítható folyamatainál az egyidejűleg történő pozitív és negatív átalakulások abszolút értékükre nézve egyenlők legyenek?
Hogy e feltétel teljesítése lehetségessé váljék, a hő munkává, vagy fordítva történő átalakulási egyenértékének meghatározásánál még egy olyan elemet is tekintetbe kell vennünk, amelyről addig nem volt szó. Ez legvilágosabban akkor tűnik ki, ha pl. az ideális gázt választjuk azon testnek, amelynek változása révén megy végbe a vizsgált átalakulás.
Legyen adva bizonyos mennyiségű ideális gáz, amely kitölt bizonyos térfogatot. Ha a gáz pl. kétszeres térfogatra terjed ki, a kezdeti és végső térfogat által teljesen meghatározott diszgregáció növekedés áll be. A kiterjedéssel egyidejűleg hő alakul át munkává. Mivel pedig ideális gáznál nincs belső munkavégzés, mert a molekulák már olyan távol vannak egymástól, hogy egymásra gyakorolt kölcsönhatásuk elhanyagolható, csak a külső nyomás ellenében végzett külső munkavégzéssel kell törődnünk, melynek nagyságát könnyen meg lehet határozni. E munka elvégzésének fedezésére szükséges hőt kívülről kell a gáznak adni, ha a hőmérsékletet állandó értéken kívánjuk tartani.
Most tételezzük fel, hogy ugyanaz a folyamat, amely szerint a gáz az eredetileg adott térfogatról kétszeresére terjed ki, még egyszer végbemegy, de magasabb hőmérsékleten. Ekkor a gáz nyomása nagyobb, mégpedig olyan mértékben, amilyen mértékben a mostani abszolút hőmérséklet magasabb az előbbinél. Ugyanebben az arányban nagyobb az elvégzett munka és az ahhoz felhasznált hő is. Tehát ez esetben, noha ugyanazzal a diszgregáció növekedéssel van dolgunk, több hő alakul át munkává, mint az első esetben. (...)
Ami a diszgregáció egyenértékét illeti, nem szükséges ezúttal bővebben kitérni arra, hogyan határozható meg. Elegendő e tekintetben egy általános tételt idézni, amely tulajdonképpen e meghatározás lényegét s egyúttal e tárgykörben végzett vizsgálataink főeredményét tartalmazza. Ez a tétel a következőképp hangzik: Minden test diszgregációja olyképpen határozandó meg, hogy a kapott érték a testnek csupán pillanatnyi állapotától függjön, s legyen független a folyamattól, mellyel a vizsgált testet jelen állapotába juttattuk. Valamely test minden reverzibilis változása esetén a fellépő diszgregáció‑változásnak és a hő egyidejű munkává alakulásának, valamint a fordított folyamatnak egyenlő, de ellentétes előjelű értékei szerepelnek, tehát algebrai összegük zérus.
Két egyidejűleg történő, előjelre nézve különböző, de abszolút értékben egyező átalakulásról el lehet mondani, hogy egymást kölcsönösen kompenzálják, ezért az imént mondottakat rövidebben így lehet kifejezni: Valamely test reverzibilis átalakulása során fellépő két folyamat egymást kölcsönösen kompenzálja.
Eddig csak kétfajta átalakulást vettünk szemügyre, de még egy harmadikat is tekintetbe kell vennünk.
Legyen újra adva egy változó állapotú test, de most tegyük fel, hogy nemcsak egyetlen állapotváltozás történik, hanem egész sornyi; s a változások úgy vannak elrendezve, hogy a test végül is kezdeti állapotába kerül vissza, azaz körfolyamatot végez.
Ha a test végül ismét kezdeti állapotában van, úgy végső diszgregációja egyenlő a kezdetivel; és ha a körfolyamatot, mint egészet tekintjük, azt mondhatjuk, hogy semmiféle diszgregáció‑változás nem történt. Ettől eltekintve, közben hő munkává, vagy munka hővé alakulhatott át.
Tegyük fel azt, hogy a test körfolyamatot alkotó állapotváltozásai térfogat‑változásokkal kapcsolatosak; a test egyik hőmérsékleten kitágul, másikon újra összehúzódik. Ha a tágulás magasabb hőmérsékleten történik, mint az összenyomódás, a kitágulásnál, fellépő munkavégzés nagyobb az összenyomódás során felhasználódó munkánál. Az egészet tekintve, a végzett munkában fölösleg mutatkozik, amelyhez természetesen megfelelő mennyiségű hőt kellett befektetni. Ha a körfolyamat fordított módon folyik le, vagyis a kitágulás alacsonyabb hőmérsékleten történt, az összenyomódásnál, úgy az összenyomásnál felhasznált munka nagyobb a kitágulás során végzett munkánál; így fölösleg mutatkozik a felhasznált munkában, minek fejében megfelelő mennyiségű hőnek kellett keletkeznie.
A körfolyamat során tehát - aszerint, hogy milyen értelemben folyik le - vagy hő alakul át munkává, vagy munka hővé. És most felmerül a kérdés, hogy ez az átalakulás az egyedüli‑e vagy egy másik kompenzációul szolgáló átalakulás is kíséri?
Először azt az esetet vizsgáljuk meg, midőn a kitágulás magasabb hőmérsékleten történik, mint az összenyomás. A kitágulás során (hogy a test hőmérsékletét az eredeti fokon tartsuk) hőt kell közölnünk a testtel, kívülről, tehát valamilyen idegen test felhasználásával. Jelöljük ez idegen hőtartályt $A$‑val. Ez fogja pótolni a kitáguláskor munkára elhasznált hőt. Ha most a körfolyamat során később a test hőmérséklete csökken és e mélyebb hőmérsékleten nyomjuk össze, hogy az összenyomáskor megtartsa alacsonyabb hőmérsékletét, kifelé, tehát egy idegen, alacsonyabb hőmérsékletű (s a továbbiakban $B$‑vel jelölt) testnek le kell adnia azt a hőt, amely a munkavégzés során keletkezik.
Ez utóbbi, az összenyomáskor a munkavégzés során keletkező s a $B$ testnek átadó hőmennyiség a fentiek szerint nem egészen akkora, mint a kitáguláskor az $A$ testből elvonódó és munkavégzésre felhasznált hőmennyiség. Ez utóbbi nagyobb az elsőnél, a többlet a körfolyamatban folyamatosan munkává alakul át. Az $A$ testből elvont hő másik részéről (ti. arról a részről, amely először munkává, azután ismét hővé alakult át), azt mondhatjuk, hogy a körfolyamat a magasabb hőmérsékletű $A$ testről az alacsonyabb hőmérsékletű $B$ testre vitte át.
A körfolyamat végeredménye tehát kettős: egy bizonyos hőmennyiség folyamatosan munkává alakul, egy másik hőmennyiség melegebb testről hidegebb testre vándorol át. Ha a körfolyamatot megfordítva végeztük volna el, akkor munka hővé alakult volna, s ugyanakkor egy másik hőmennyiség hidegebb testről melegebb testre ment volna át.
Látjuk tehát, hogy a körfolyamatban a hőnek munkává, vagy a munkának hővé való átalakulása egymagában nem fordul elő. Ezt az átalakulást mindig egy másik folyamat kíséri: a hő melegebbről hidegebb testre, ill. hidegebbről melegebb testre megy át. Kézenfekvő ezt a hőátmenetelt az átalakulás kompenzációjának tekinteni."
6. Az egyensúly különböző típusai. Az önreguláció szerepe a hőelméletben
Megállapítottuk, hogy a hőjelenségek végső fokon ún. kiegyenlítődési folyamatok: a fizikai rendszer minden. egyes intenzitásmennyisége a rendszeren belüli azonos érték felvételére törekszik. A közös érték beállásával az egyensúly is beáll. Ily módon, ha egy rendszeren belül hőmérséklet, nyomás, elektromos potenciál, kémiai potenciál stb. - különbségek vannak, olyan irányú energiaáramlás indul meg, amely a különbségek megszűnését vonja maga után. Az egyensúlyi állapotban levő rendszerben a hőmérséklet, a nyomás, az elektromos potenciál, a különböző kémiai anyagokhoz tartozó kémiai potenciálok mindenütt azonos értékűek. Röviden: az egyensúly szükséges és elegendő feltétele a megfelelő intenzitásmennyiségek egyenlősége.
A kiegyenlítődés mindig meghatározott irányt szab a folyamatoknak. Ezek tehát önként csak egyik irányban mehetnek végbe, a fordított irányban nem. Szokásos szakkifejezéssel élve, a hőfolyamatok nem‑megfordíthatóak, irreverzibilisek. Az irreverzibilitás, megfordíthatatlanság egységes mértéke - valamennyi kölcsönhatási típust tekintve - az entrópia növekedése. Más szóval, a természetben önként csak entrópianövekedéssel együtt járó folyamatok mehetnek végbe. Midőn az intenzitásmennyiségekben fennálló különbségek kiegyenlítődtek, tehát midőn az egyensúly beállt, az entrópia elérte maximális értékét. Röviden: egyensúlyi állapotban az entrópia értéke maximális.
Egyensúly azonban többféle van. Az egyensúlyi állapotokat aszerint osztályozhatjuk, hogy az egyensúly megzavarása után a rendszer hogyan viselkedik. Az osztályozás könnyebb érthetősége kedvéért először egy egyszerű mechanikai egyensúlyi problémával foglalkozunk.
Láttuk, hogy a Föld nehézségi erőterében levő testek olyan helyzetet igyekszenek elfoglalni, melyben helyzeti energiájuk minimális. E minimális energiaérték természetesen a fennálló körülmények megengedte lehetőségek mellett tekintendő. Pl. az asztallapon levő tárgy nem tud tovább esni, mivel az asztal lapja megakadályozza e törekvés megvalósulását. Az adott feltételek mellett a tárgy számára ez a minimális helyzeti energia: a tárgy az asztal felületén egyensúlyban van. Ilyenfajta egyensúlyok háromféle típusát különböztethetjük meg, a különböző típusokat először egy-egy példán mutatjuk be.
Vizsgáljuk meg egy tárgynak a következő háromféle helyzetét:
1. Helyezzük a tárgyat egy hegy csúcsára, az ábrán látható módon. (8. ábra, a.) A tárgy az adott feltételek mellett egyensúlyban van, de ha csak egy kicsit is meglökjük, legurul a völgybe. Az ilyenfajta egyensúlyi állapotot az jellemzi, hogy nagymértékben bizonytalan: a legkisebb zavar is elegendő ahhoz, hogy a test egészen új, az eredetitől messze eső állapotba menjen át. Mindazon egyensúlyi állapotokat, melyeknél - bármiféle zavar esetén - a test az eredeti állapottól eltávolodni igyekszik, bizonytalan (labilis) egyensúlyi állapotnak nevezzük.
2. A vízszintes asztallapra helyezett tárgy helyzete az előbbitől eltérő egyensúlyi állapotot képvisel (8. ábra, b.) ha az asztallapon levő tárgyat egy kissé arrább helyezzük, ott ugyancsak egyensúlyban marad. Az olyan egyensúlyi állapot, amelynek szomszédos állapotai is egyensúlyiak, az ún. semleges (neutrális) egyensúly.
3. Végül, ha a völgy legmélyebb pontján elhelyezett tárgyat (8. ábra, c.) kimozdítjuk helyzetéből, azt tapasztaljuk, hogy az igyekszik megtartani eredeti egyensúlyi állapotát, igyekszik visszatérni eredeti helyére, a völgy legmélyebb pontjára. Minden olyan egyensúlyi helyzetet, melyben az egyensúlyi állapotban levő tárgy igyekszik megtartani eredeti állapotát, biztos (stabilis) egyensúlynak nevezzük.
A fenti egyszerű példa jellegzetességei általánosságban is érvényesek, bármilyen természetű fizikai egyensúlyról van is szó. Ezek szerint háromféle egyensúlyt kellene a hőelméletben is megkülönböztetni. Azért mondjuk, hogy kellene, mert a hőelméletben a semleges egyensúly egyáltalán nem lép fel, a bizonytalan egyensúly pedig csak ritkán. A hőelméletben szereplő egyensúlyi állapotok többnyire stabilisak.
Bizonytalan (labilis) egyensúlyi állapotban vannak az ún. túlhűtött vagy túlhevített testek. Ismeretes, hogy a hőmérséklet és a nyomás megfelelő változtatásával a testek halmazállapota előírt hőmérséklet és nyomásérték mellett megváltozik. Előfordulhat azonban, hogy a változás mégsem megy végbe. Így pl. a víz kivételesen lehűthető ($1\ \mathrm{atm.}$ nyomás mellett) $0\ \mathrm{{}^\circ C}$ alá, anélkül, hogy megfagyna. Vagy: az óvatosan hűtött oldatból, a törvényszerű hőmérsékleten nem válnak ki kristályok. Az ilyenfajta egyensúlyok mindig bizonytalanok, ha a rendszert kissé megzavarjuk, lavina‑szerűen megindul az elmaradt halmazállapot kialakulása. Így pl. ha a túlhűtött oldatot kissé megrázzuk, vagy kis jégdarabot dobunk bele, hirtelen megindul a fagyás. A túltelített oldat hasonlóképp viselkedik: kis zavarás is elegendő ahhoz, hogy egyszerre meginduljon az oldott anyag kristályainak lavinaszerű képződése. Az üvegek szintén túlhűtött folyadékok, melyek látszólagos szilárdsága onnan származik, hogy igen nagy a belső súrlódásuk. Az üvegek egyensúlya tehát bizonytalan, és ennek megfelelően idővel kristályos állapotba mennek át. Az üveg kristályosodása kedvezőtlenül befolyásolja az egyébként kívánatos tulajdonságokat, így azokat tekintjük jó üvegnek, amelyek csak igen hosszú idő után, tehát viszonylag lassan veszik fel a kristályos állapotot. Mint látjuk, az instabil egyensúlyi állapotok között az üveges állapot szélsőséges esetet képvisel, amennyiben a változás csak igen lassan megy végbe. A lényeges vonás azonban mégis megvan, ugyanis az állapot fokozatosan távolodik az eredeti állapottól, és a bizonytalan egyensúlyt éppen ez a tulajdonság jellemzi.
A hőegyensúlyok nagy része stabilis. A biztos egyensúly fenntartásának sajátos mechanizmusa van, melyet először a hőelméletben ismertek fel, de amelynek érvénye messze túlnő a hőelmélet keretein. A továbbiakban e sajátos mechanizmussal ismerkedünk meg.
Bizonyára legtöbb olvasó találkozott már életében olyan gőzgéppel, melynek egyenletes működését egy kétkarú forgó szerkezet szabályozza. A gőzgép működése esetében az egyensúlyt a lendítőkerék egyenletes fordulatszáma jelenti, az egyensúly biztosságát pedig az, hogy az eredeti fordulatszám kisebb zavarok hatására nem változik meg. A hajtóerőt szolgáltató gőznyomás nyilvánvalóan nem egyenletes. Nagyobb nyomás esetén nagyobb, kisebb nyomás esetén pedig kisebb a fordulatszám. A fordulatszám‑ingadozások elkerülését a gőznyomás egyenletességének biztosításával, ezt pedig egy szeleppel biztosíthatjuk, a következőképpen. Ha átmenetileg megnövekszik a gőznyomás, a fordulatszám megemelkedik. Ekkor a regulátor fordulatszáma is megnő. Ennek megfelelően a forgó súlyzókra ható centrifugális erő is növekszik, a súlyzókarok felemelkednek, és megnyitják a szelep nyílását, melyen át gőz távozik el; így csökken a gőztérben a nyomás, vele együtt a fordulatszám is. A forgó regulátorban tehát a gőznyomás változásának hatására mindig olyan irányú változás megy végbe, amelyik az eredeti gőznyomás eltolódásának nagyságát csökkenteni igyekszik.
Hasonló természetű önregulációval találkozunk a biztos hőegyensúly esetén is. Mielőtt az általános törvényszerűséget kimondanánk, néhány példán szemléltetjük a tétel jelentését. Az edénybe zárt gáz állapotát nyomása és hőmérséklete egyértelműen meghatározza. Legyen e gáz környezetével egyensúlyban, azaz nyomása és hőmérséklete legyen azonos a környezet nyomásával és hőmérsékletével. Zavarjuk meg most már a rendszer egyensúlyát:
1. oly módon, hogy az edénybe zárt gáz eredeti hőmérsékletét akár hűtéssel, akár melegítéssel megváltoztatjuk.
2. oly módon, hogy eredeti nyomását növeljük vagy csökkentjük.
Mindkét esetben megbomlik az egyensúly, hiszen az 1. alkalommal a hőmérséklet, a 2. alkalommal pedig a nyomás más‑más értékű a rendszerben és annak környezetében. Ahogyan az egyensúly megbomlik, azonnal megindul a kiegyenlítődés folyamata, éspedig az első esetben a hőmérséklet, az utóbbiban a nyomás kiegyenlítődése.
Mi biztosítja mármost azt, hogy a beálló közös hőmérséklet, ill. nyomás az eredeti egyensúlyi érték közelében maradjon? A hőelméleti jelenségek automatikusan biztosítják az egyensúly stabilitását; a hőelméleti törvényekben pedig már eleve megadjuk az önreguláció jellemzését is. Tudniillik:
1. hőmérsékleti egyenlítődés esetén az entrópia növekedése csak úgy következhet be, ha a nyomás is megváltozik, éppen oly módon, hogy ezáltal az eredeti hőmérsékletkülönbség csökken;
2. nyomáskiegyenlítődés esetén csak a hőmérséklet segítő változása révén tud a kiegyenlítődés minél gyorsabban végbemenni.
Az önregulációnak számtalan hasonló példájával találkozhatunk a mindennapi életben is. A nyitott edénybe tett víz párolog. A párolgás viszont a hőmérséklet csökkenésével jár, a hőmérséklet csökkenése - továbbá - a párolgást csökkenti. Tehát a párolgás folyamata önmagát fékezi.
A fenti egyes esetekben megnyilvánuló közös törvényszerűséget Braun és Le Chatelier ismerték fel még a múlt században. Korszerű megfogalmazásban a törvény így szól:
Bármely intenzitásmennyiség megváltoztatásával idézzük is elő az egyensúly megbomlását, a megváltoztatott intenzitás‑mennyiségnek a többi segítségére siet oly módon, hogy a zavarás mértéke csökkenjen. Szokás ezt az elvet a kényszer elől való menekülés elvének is nevezni, éppen ezért, mivel a kikényszerített változásokra a test tulajdonságai úgy reagálnak, mintha a test céltudatosan ki akarna térni a változást keltő ok hatása elől. Igen lényeges az a körülmény is, melyet az előbbiekben szintén említettünk, hogy tudniillik az önreguláció nem más, mint az entrópianövekedés tételének szükségszerű velejárója.
Ez utóbbi körülményt igen szépen szemléltethetjük az alábbi grafikus ábrázolásban bemutatott példákon. Ha grafikusan ábrázoljuk a nyomásnak a térfogattól való függését rögzített entrópiaérték mellett, az alábbi görbét kapjuk: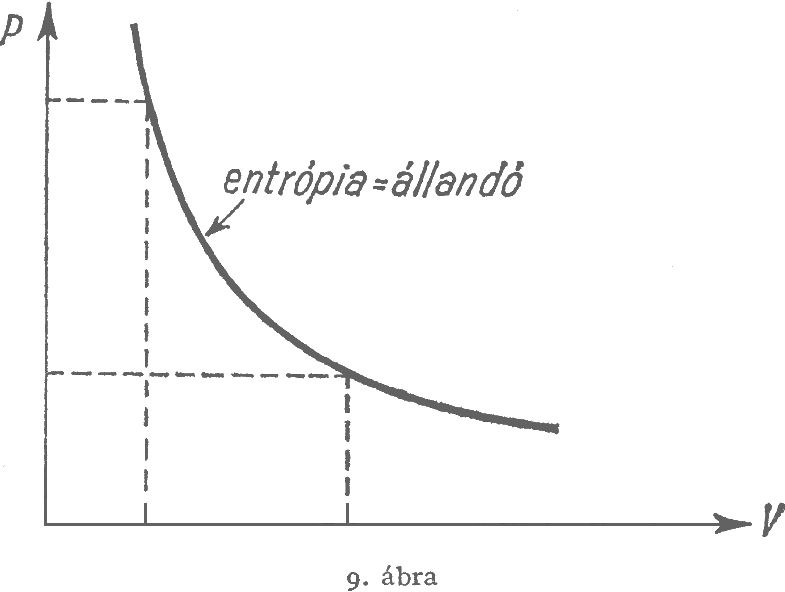
A kihúzott görbe által egymáshoz rendelt nyomás‑térfogat értékpárok itt mind azonos entrópiaértéket határoznak meg. Rajzoljuk most fel ugyanezt a kapcsolatot azzal a különbséggel, hogy az entrópia helyett a hőmérséklet állandóságát kényszerítjük rá a rendszerre:
Itt a kihúzott vonalra eső állapotok mind ugyanazon hőmérséklethez tartoznak. A kétféle ábrát egymásra kopírozva azt tapasztaljuk, hogy a nyomás‑térfogat diagram állandó entrópiaérték mellett meredekebben esik, mint állandó hőmérséklet mellett:
Vagyis, ha a hőmérsékletet rögzítjük, és így megakadályozzuk "segítő" szerepének bekövetkezését, a nyomáskiegyenlítődés lassabban megy végbe.
Az állandó entrópiához és az állandó hőmérséklethez tartozó diagram fenti tulajdonsága azt is jelenti, hogy a két görbe csupán egyetlen pontban metszheti egymást. Ugyanis, ha második metszéspont is lehetne, akkor a görbék meredekségének is szerepet kellene cserélni. A 12. ábrán pontozott vonallal jelöltük a képzeletbeli ágat, mely újabb metszéspont fellépéséhez vezetne:
Látjuk, hogy a képzeletbeli (de valójában nem létező) második metszéspontban már az állandó hőmérséklet diagramja volna meredekebb, ami viszont ellentmond az entrópiatételnek. Ez utóbbi megjegyzést magyar vonatkozású történeti érdekessége miatt tettük: Farkas Gyula, az 1931‑ben elhunyt magyar elméleti fizikus éppen e szabályszerűség felismerése alapján jutott el 1895‑ben az entrópia‑tétel szabatos megfogalmazásához, megelőzve ebben minden más kutatót. Farkas Gyula megfogalmazásában tehát a hőelmélet II. főtétele így szól: egyetlen test sem hozható hőhatástól mentesen (állandó entrópia) oly állapotba, melybe pusztán a hőmérséklet megváltozásával juthat.
A stabilis egyensúlyban megzavart rendszer, mint láttuk, sajátos természeti törvénynek engedelmeskedve éri el az egyensúly fenntartását. Célszerű ellesni és alkalomadtán mesterségesen alkalmazni a természetnek e szép törvényszerűségét. A hőelmélet és a kibernetika kapcsolatát éppen az önreguláció törvényeinek közös formája biztosítja.
Az entrópia‑fogalommal való ismerkedésünk kapcsán elkerülhetetlenül előkerülnek a hőelmélet más fontos fogalmai és tételei is. Bár jelen kereteken belül nem feladatunk a hőelmélet ismertetése, a teljesség kedvéért röviden megemlékezünk azokról az alapvető megállapításokról is, amelyeken ez az egész tudományág nyugszik. Ezen alapvető megállapításokat a termodinamika főtételeinek hívjuk. Jelenleg négy főtételt tartunk számon, melyek közül kettő időben lényegesen megelőzte a többit: az első és a második főtétel. A harmadik csak a század elején vált ismeretessé, végül az időben negyedikként kimondott főtétel csak az utóbbi évtizedek szülötte. Azonban a "negyedik" sorszám sehogysem illik e tételre, mivel logikai szempontból megelőzi az összes többit, így - Guggenheim javaslatára - a "nulladik főtétel" elnevezést kapta. Az alábbiakban vázlatosan áttekintjük a négy főtétel fogalomkörét, megemlítve néhány jellegzetes következményüket is.
$\ast $
A nulladik főtétel a termodinamikai egyensúlyra vonatkozik: az egyensúly szükséges és elégséges feltétele az egyes közelhatásokhoz tartozó intenzív mennyiségek kiegyenlítettsége. Ezzel a főtétellel az előbbiekben már találkoztunk, foglalkozzunk most egyik igen jelentős következményével, a Gibbs‑féle fázisszabállyal.
Előfordulhat, hogy a több egynemű egységből (termodinamikai testből) álló rendszeren belül bizonyos testek minden fizikai és kémiai tulajdonsága megegyezik. Ezeket egyetlen fázis különböző képviselőinek tekintjük. A termodinamikai egyensúly szempontjából elegendő csupán a különböző fázisokat megkülönböztetni. Pl. $0\ \mathrm{{}^\circ C}$ hőmérsékletű vízben számos különálló jégdarab úszik; e jégdarabokat - még akkor is, ha számuk több egynél - egyetlen fázisként tartjuk nyilván: az egész rendszer csupán két fázisú.
A termodinamikai rendszerek többféle kémiai anyag keverékei lehetnek, többféle kémiai komponensből állhatnak. Bizonyos számú komponens együttese olyan kémiai átalakuláson mehet keresztül, hogy végeredményben megnövekszik a komponensek száma. Az állapot egyértelmű jellemzéséhez azonban elegendő csupán azt a minimális számú anyagot figyelembe venni, amelyikből a szóban forgó rendszer előállítható. Ezek a független komponensek. A fázisok számát $N$‑nel, a független komponensek számát $K$‑val jelöljük. A rendszeren belül fellépő közelhatások száma legyen $I$. Alapvető tapasztalat, hogy $I$ számú közelhatás fellépése mellett minden egyes test állapota $I$ számú adattal jellemezhető. (Pl. az egyes közelhatásokhoz tartozó extenzív mennyiségek.) Az $N$ fázisú rendszer összes adatainak száma tehát $I\cdot N$. Egyensúly esetén ez adatok nyilván nem mind függetlenek egymástól, a megfelelő intenzív mennyiségeknek az egyes fázisokra vonatkozó azonossága $I\cdot (N-1)$ számú összefüggést szolgáltat: Az $I$ számú közelhatás mindegyikéhez tartozik ilyen $N-1$ számú összefüggés, tehát összesen $I(N-1)$. Ha ezt levonjuk az összes adatok számából, az $I\cdot N$-ből, úgy a független adatok számát, a rendszer szabadsági fokszámát kapjuk, amit $f$‑el jelölve
$$f=I\cdot N-I(N-1)=I\cdot N-I\cdot N+1$$
$$f=I$$
Egyensúlyi rendszer szabadsági fokszáma megegyezik a közelhatások számával. Ez a Gibbs‑féle fázisszabály, mely a többfázisú rendszerek egyensúlyának vizsgálatában gyakorlati szempontból is fontos szerepet játszik.
$\ast $
Az első főtétel az energia megmaradásának elvét mondja ki: a belső energia megváltozása a hő és munka összege:
$$\Delta E=\Delta Q+\Delta W$$
Az előzőekben már mondottuk, hogy csupán térfogatmunka fellépésekor
$$\Delta W=-p\cdot \Delta V$$
ahol $p$ a nyomás és $\Delta V$ a térfogatváltozás. Ezt figyelembe véve, a hőhatás így írható
$$\Delta Q=\Delta E+p\cdot \Delta V$$
Mivel a hőhatás nagyságát két egymástól független állapothatározó változása szabja meg és mivel p mindkét állapothatározótól $(E$ és $V)$ függhet, a kezdeti és végállapot nem szabja meg egyértelműen a $\Delta Q$ értékét. A hő nagysága csak akkor egyértelműen adott, ha egy állapothatározó (pl. akár $V$, akár $p$) értéke a folyamat kapcsán rögzített. Állandó $V$ mellett történő változásoknál
$$\Delta Q=\Delta E$$
és állandó $p$ mellett
$$\Delta Q=\Delta (E+pV)=\Delta H$$
$$H=E+p\cdot V$$
mennyiséget hőtartalomnak vagy entalpiának nevezik. (Entalpia = állandó nyomáson felvett hő.)
A testek hőkapacitását a hő és az előidézett hőmérséklet‑változás viszonyával szokták számszerűen jellemezni:
$$c=\frac{\Delta Q}{\Delta T}$$
Mivel az állapotváltozás nincs egyértelmű kapcsolatban a hőhatás nagyságával, a viszonyszám is határozatlan. Ezzel szemben az állandó térfogaton történő hőfelvétel már egyértelműen a belső energia megváltozásával azonos, így az állandó térfogathoz tartozó hőkapacitás a belső energia- és a hőmérséklet‑változás viszonya
$$c_V=\frac{\Delta E}{\Delta T}$$
Hasonlóképp belátható, hogy az állandó nyomáshoz tartozó hőkapacitás a hőtartalom és a hőmérsékletváltozás viszonya
$$c_p=\frac{\Delta H}{\Delta T}$$
A különböző fázisátalakulások és kémiai átalakulások egy része hőfejlődéssel jár; (ezek az exoterm folyamatok.) Más része a környezetből való hőelvonással (endoterm folyamatok). A fejlődő ill. elveszett hőt átalakulási hőnek nevezzük. Mivel a hőfejlődés az átalakuláson átment test szempontjából veszteséget, a környezetből való hőelvonás nyereséget jelent, a folyamat hőtermelése ellenkező előjelű a test hőhatásával szemben:
$$\mathrm{átalakulási\ hő}=-\Delta Q=-\Delta E-p\cdot \Delta V$$
Az előbb kifejtett indokok szerint az átalakulási hő is csak akkor egyértelmű, ha az átalakulás bizonyos állapothatározók rögzített értéke mellett megy végbe. Írjuk az utóbbi mérlegegyenletet számunkra alkalmasabb formában. A kezdeti fázis ill. kémiai összetétel mellett jelezzük a test adatait I‑el, a végállapotba jutott rendszer adatait pedig II‑vel. Ekkor az
$$\mathrm{átalakulási\ hő}=-(E_{\mathrm{II}}-E_{\mathrm{I}})-p(V_{\mathrm{II}}-V_{\mathrm{I}})$$
Így az állandó térfogaton végbemenő átalakulás $(V_{\mathrm{I}}=V_{\mathrm{II}})$ hője
$$Q_V=-(E_{\mathrm{II}}-E_{\mathrm{I}})=E_{\mathrm{I}}-E_{\mathrm{II}}$$
és hasonlóképp állandó nyomás mellett
$$Q_p=-(H_{\mathrm{II}}-H_{\mathrm{I}})=H_{\mathrm{I}}-H_{\mathrm{II}}$$
A $Q_V$, és $Q_p$ adatok az I. állapotbeli hőmérsékletre vonatkozva értendők. Ez azt jelenti, hogy az átalakulás után (közben a hőmérséklet is megváltozott) a II. rendszert visszavisszük az eredeti hőmérsékletű állapotba, $Q_V$, és $Q_p$ az eközben leadott (exoterm folyamat) ill. felvett (endoterm folyamat) hőt jelenti. ily módon $Q_V$, az eredeti hőmérsékletre és térfogatra, $Q_p$, pedig az eredeti hőmérsékletre és nyomásra vonatkoztatva értendő.
Az átalakulási hő maga is függhet a hőmérséklettől. E függést Kirchoff egyik törvénye fejezi ki. Hogy miként, azt az eddig mondottak alapján könnyen meg tudjuk állapítani. Hajtsuk végre az átalakulási folyamatot először $T$ hőmérsékleten, aztán pedig $T+\Delta T$ hőmérsékleten. Az átalakulási hők különbsége
$$\Delta Q_V=\Delta E_{\mathrm{I}}-\Delta E_{\mathrm{II}}$$
$$\Delta Q_p=\Delta H_{\mathrm{I}}-\Delta H_{\mathrm{II}}$$
ahol $\Delta E_{\mathrm{I}}$, $\Delta E_{\mathrm{II}}$, $\Delta H_{\mathrm{I}}$, $\Delta H_{\mathrm{II}}$ az I, ill. II. testek belső energiájának ill. hőtartalmának $\Delta T$ hőmérséklet‑változásra eső változásai, amiket $\Delta T$‑vel osztva éppen a hőkapacitásokat nyerjük.
Így
$$\frac{\Delta Q_V}{\Delta T}=c_{\small V\normalsize \mathrm{I}}-c_{\small V\normalsize \mathrm{II}}$$
$$\frac{\Delta Q_p}{\Delta T}=c_{p\mathrm{I}}-c_{p\mathrm{II}}$$
Kirchoff tétele szerint, tehát a hőkapacitás megváltozása éppen az átalakulási hő és a hőmérséklet megváltozásának hányadosával egyenlő.
$\ast $
A második főtétel egyrészt az entrópia létezését, másrészt az entrópianövekedés és a kiegyenlítődésre való törekvés törvényét mondja ki.
Mondottuk, hogy a $\Delta Q$ nagyságát az állapothatározók megváltozása nem határozza meg egyértelműen, de van olyan mennyiség, amelyikkel $\Delta Q$‑t elosztva, már az állapottól egyértelműen függő mennyiség változását kapjuk:
$$\frac{\Delta Q}{\tau }=\Delta \sigma,\ \ \tau \neq 0$$
ahol a $\tau $ osztó (mely zérus nem lehet) az állapothatározók függvénye és a az ún. empirikus entrópia. Ez az összefüggés általánosabb, mint az eddigiekben szereplő:
$$\frac{\Delta Q}{T}=\Delta S,\ \ T\neq 0$$
ahol $T$ az abszolút hőmérséklet és $S$ az abszolút entrópia. Miben áll a két - látszólag azonos - meghatározás különbsége? A továbbiakban csupán ezzel a kérdéssel foglalkozunk, hiszen a második főtétel más részleteivel már megismerkedtünk.
Háromféle mennyiség szerepel meggondolásainkban: a hőmérséklet, az entrópia és a $\tau $‑val jelzett osztó. Kapcsolatuk alapos megvizsgálása világítja meg az abszolút hőmérséklet fogalmát. A hőmérséklet a hőhatás intenzív mennyisége. Ha két test hőmérséklete egyenlő, úgy termikus egyensúlyban vannak egymással; ha különböző, a nagyobbik hőmérsékletű testről energia áramlik a kisebb hőmérsékletű felé mindaddig, míg a különbség ki nem egyenlítődik. Voltaképp ez a törvényszerűség értelmezi a hőmérsékletet. Nyilvánvaló azonban, hogy az értelmezés nem egyértelmű. Miben áll a többértelműség? Tekintsünk két testet és állapítsuk meg tapasztalatilag, mely állapotban vannak egymással termikus egyensúlyban, másként: mely állapotban egyenlő a hőmérsékletük? Az energiaáramlás irányából még a nagyobb hőmérséklettel rendelkező állapotokat meg tudtuk különböztetni a kisebbektől, de hogy milyen értékkel bír egy‑egy közös hőmérsékletnek megfelelő állapot és hőmérsékletkülönbség esetén mennyivel nagyobb egyik a másiknál, azt semmiféle törvény nem szabályozza. Röviden: bizonyos megszorításoktól eltekintve a hőmérsékleti skála önkényes, végtelen sok választási lehetőségünk van. A 13. ábrán a feltüntetett hőmérsékleti pontok számszerű jellemzését kétféleképp is megadjuk, mindkét fajta számozás jogos, ha az egyik az (l. 13. ábra, a.). Az ilyen önkényes beosztású skálát nevezzük empirikus hőmérsékleti skálának. A skálatörvény megválasztásán kívül a nullapontot és az egységet is meg kell adnunk. A további két skála (l. 13. ábra, b.) fele akkora egységgel bír.
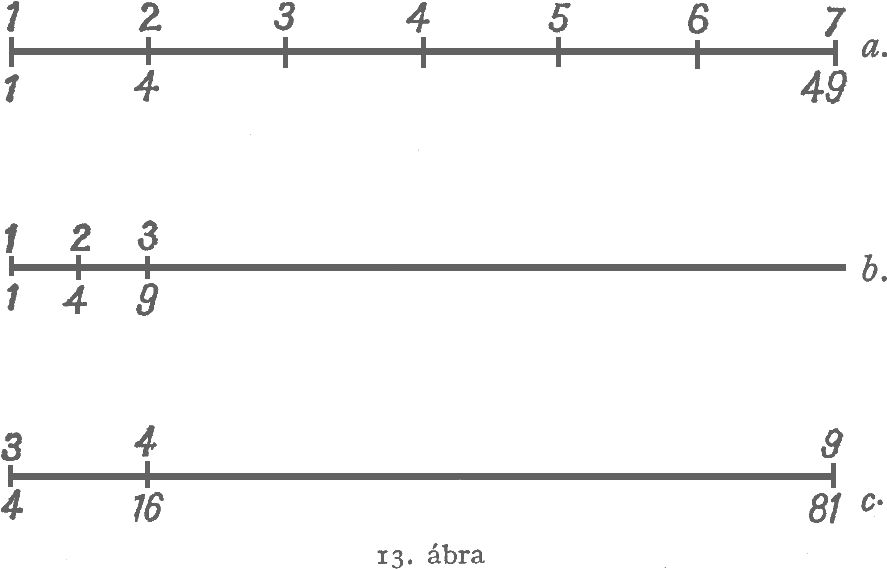
Más nullapont választásával (másutt kezdjük a számozást), de pl. az eredeti egységgel, (l. 13. ábra, c.) a bemutatott skálát kapjuk. A bemutatott egyszerű példák világosan mutatják, mit jelent a skálatörvény, az egység és a nullapont a hőmérséklet számszerű jellemzése szempontjából. Ebből az is látszik, hogy a Celsius, Réaumur, Fahrenheit és Kelvin‑skála mindegyike azonos skálatörvényt követ, csupán az egység és a nullapont megválasztásában különböznek egymástól.
A hőmérsékleti skála önkényességét a következő törvény szünteti meg: a végtelen sok lehetséges empirikus skála és a végtelen sok lehetséges $\tau $ osztó között van egy közös: olyan mennyiség, amelyik hőmérsékleti skálaként és a $\Delta Q$ változást egyértelművé tevő osztóként egyaránt használható. Ez az abszolút hőmérséklet. A Carnot‑féle körfolyamattal kapcsolatban láttuk, hogy a $T$ abszolút hőmérséklet minden testre nézve azonos előjelű (pl. pozitív), így az abszolút skálában előjelváltás nem léphet fel. Ez utóbbi körülmény a nullapont megfelelő rögzítésével érhető el. A nullapont viszont nem értelmezhető, hiszen $\tau =T=0$ mint a $\Delta Q$ osztója zérus sohasem lehet. Az abszolút hőmérséklet nullapontja nem létezik, így nincs is olyan állapot, amelyikben $T=0$ volna.
$\ast $
Ezzel már áttértünk a hőelmélet harmadik főtételének problémakörére. A termodinamika harmadik főtétele szerint egyrészt az abszolút zéruspont elérhetetlen, másrészt a kémiailag tiszta (egynemű) cseppfolyós és szilárd (kondenzált) anyagi rendszerek entrópiája zérushoz közeledik, ha abszolút hőmérsékletük zérushoz tart. (Megjegyzendő, hogy ugyanekkor a testek hőkapacitása is zérushoz tart.)
A hőelmélet főtételei, szükségszerűen beleértve a harmadik főtételt is, lehetővé teszik a kémiai rokonságnak (affinitás), tehát bizonyos anyagok vegyülésre való törekvésének számszerű jellemzését. A harmadik főtétel alkalmazásaként végül még ezzel a kérdéssel foglalkozunk.
A hőelmélet molekuláris értelmezése szerint a testek belső energiája a molekulák mozgási energiájából és a molekulák egymásra gyakorolt erőhatásával kapcsolatos potenciális energiájából tevődik össze. A belső energiába tehát nem számít bele a molekulák belső szerkezetéhez tartozó energia. Midőn kémiai átalakulás történik, más szerkezetű molekulák keletkeznek, megváltozik tehát a szerkezeti energia is. Világos azonban, hogy az energia megmaradásának tétele szerint a termikus belső energia és a molekuláris szerkezeti energia összege állandó. Így, ha az átalakulás olyan molekulákat eredményez, melyekben kevesebb szerkezeti energia van felraktározva, mint előzőleg, úgy a termikus belső energia nő; ha pedig a molekulák átalakulás eredményezte új szerkezeti energiája nagyobb, mint eredetileg volt, úgy a többlet a termikus belső energiából fedeződik. A molekuláris szerkezeti energia megváltozását közvetlenül az a munka méri, amelyet végezni kell a régi szerkezetű molekuláknak új szerkezetűekké való átalakítása érdekében. Így a folyamat akkor megy magától végbe, ha az átalakulás kifele irányuló munkavégzést eredményez, különben pedig annál nehezebb létrehozni a folyamatot, minél nagyobb munkát kell kívülről befektetni. Az előbbi esetben az affinitás pozitív, utóbbi esetben negatív. A szóban forgó munkavégzést el kell különítenünk a termodinamikai állapothatározók megváltozása folytán fellépő térfogati munkától, a munka tehát két részből áll: az átalakulás eredményezte "hasznos" munka $\Delta W$ és a térfogatmunka $-p\cdot \Delta V$. Így az első főtétel szerint adódó energiamérleg (a folyamat energiatermelése és nem a rendszer energianyerése szempontjából megítélve) már az affinitás mértékét adja
$$\Delta E=\Delta W-p\cdot \Delta V+\Delta Q$$
$$\mathrm{affinitás}=A=-\Delta W=\Delta E-p\cdot \Delta V+\Delta Q$$
Vegyük még figyelembe azt is, hogy
$$\Delta Q=T\cdot \Delta S$$
így
$$A=-\Delta W=-\Delta E-p\cdot \Delta V+T\cdot \Delta S$$
A nyert mérték ilyen formában azonban még nem egyértelmű (l. az átalakulási hő értelmezését), de $T$ és $V$ ill. $T$ és $p$ rögzített értéke mellett már egyértelművé válik. Végül is az affinitás a reakcióhőből úgy nyerhető, hogy levonjuk belőle az entrópiaváltozásnak a hőmérséklettel való szorzatát:
$$A_V=Q_V-T(\varphi_{\mathrm{I}}-\varphi_{\mathrm{II}})$$
$$\mathrm{illetve:}$$
$$A_p=Q_p-T(\varphi_{\mathrm{I}}-\varphi_{\mathrm{II}})$$
Ebből már az affinitások abszolút mérőszámait is meghatározhatnánk, ha az entrópia abszolút mérőszámát ismernénk. A harmadik főtétel nélkül az entrópia határozatlan összeadandót tartalmaz, így az entrópia határozatlan volna. A harmadik főtétel szerint viszont az állandó értéke úgy rögzítendő, hogy az abszolút nullaponton maga az entrópia is zérus legyen. Ezáltal pedig nemcsak az entrópia, hanem az affinitások nullaponti értéke is rögzítődik.
III. AZ ENTRÓPIA STATISZTIKUS JELENTÉSE
1. Az anyag molekuláris szerkezetének hőelméleti jelentősége
Az összefüggő anyag (a szilárd, cseppfolyós és légnemű testek) felépítése látszólag folytonos. Manapság azonban már közismert, hogy az anyag molekuláris szerkezetű. A molekulák térbeli mérete és tömegük igen kicsiny, így már kis anyagmennyiségben is igen sok részecske van. A sok azonos természetű részecske által alkotott rendszer jellemzésmódjára önként ajánlkozik a statisztikus módszer. Ezért nincs abban semmi csodálatos, hogy az anyag szerkezeti felépítését leíró törvények statisztikus jellegűek és statisztikus természetűek a hőelméleti törvények is.
A hőelméleti törvények statisztikus értelmezése kapcsán különösen fontos szerepe van az entrópiafogalom statisztikus jelentésének, éppen ezért a továbbiakban ezzel foglalkozunk legtöbbet. A többi kérdés tárgyalására csupán e főprobléma megértésének érdekében térünk ki.
A statisztikus hőelmélet mechanikai természetű egyedekből álló sokaságokon végbemenő tömegjelenségekkel foglalkozik, felhasználva a valószínűségszámítás módszereit. Az individuumok maguk is összetettek lehetnek, meghatározott szerkezettel rendelkezhetnek.
A szóban forgó tömegjelenségek nem egyebek: klasszikus, ill. kvantummechanikai többtestproblémák, ahol az egyedek száma igen nagy ahhoz, hogy a szokásos mechanikai ill. kvantummechanikai megoldási módszereket gyakorlatilag elvégezhető módon tudjuk alkalmazni. Azonban elvben semmi akadálya nincs az egzakt tárgyalásnak. Ettől a lehetőségtől azonban számolási nehézségek miatt mégis kénytelenek vagyunk eltekinteni és helyette valószínűségszámítási tárgyalásmódot alkalmazni. A statisztikus mechanika létjogosultságát (ti. mint szükségmegoldást) részben ez a körülmény indokolja, de nem ebben áll a dolog lényege. Valójában ugyanis nem egyes individuumok viselkedése, hanem maga a tömegjelenség szolgálhat a közvetlen megfigyelés tárgyául. (Pl. folyadéksűrűség, hőmérséklet, nyomás, entrópia stb.) Hiába ismernénk egy anyagi rendszer összes molekuláinak helyzetét és impulzusát, ez a hatalmas méretű adathalmaz kevesebbet mondana számunkra, mint pl. a rendszerben uralkodó nyomás és hőmérséklet ismerete.
A statisztikus hőelméletben szereplő individuumok rendszerint molekulák (ill. atomok, ionok, elemi részek). Ez azonban nem jelenti azt, hogy a statisztikus mechanika megállapításait és módszereit ne lehetne alkalmazni más esetekben is. (Pl. különböző kvantált terek kvantumainak statisztikája, kolloid rendszerek, folyó- és szélhordalékok stb.) A vizsgálati tárgy sokfélesége folytán a statisztikus hőelmélet (vagy még általánosabban: a statisztikus fizika) több résztudományt foglal magában.
De nemcsak a vizsgálat tárgya, hanem az alkalmazható valószínűségszámítási szkémák sokfélesége is szerteágazóvá teszi ezt a problémakört.
A legmélyebbre nyúlnak és így legnagyobb teljesítőképességgel rendelkeznek azok a módszerek, amelyek a sokaságot alkotó egyedek fizikai (mechanikai) viselkedésének törvényszerűségeit teljes egészükben igyekeznek felhasználni. Ide tartoznak a molekuláris‑kinetikus elméletek, pl. a Maxwell‑Boltzmann‑féle kinetikus gázelmélet és újabban Born és Green kinetikus elmélete. Ezekben az elméletekben minden makroszkopikus fogalom mélyebb, a szerkezeti felépítettségen alapuló (mikrofizikai) értelmezést nyer.
Lényegesen egyszerűbb, de kevesebbet mondó szkémák azok, amelyek a szerkezeti tulajdonságokat elhanyagolva csupán a szerkezet tényét veszik figyelembe. Ezek az elméletek kénytelenek felhasználni a fenomenologikus elmélet bizonyos fogalmait és törvényeit, figyelembe véve természetesen, hogy ezek a törvények és fogalmak statisztikus jellegűek. Nagyon jó példa erre a statisztikus termodinamika, melyben közvetlen statisztikai értelmezést csak az entrópia nyer, és a többi fogalom csak annyiban, amennyiben összefügg az entrópiával. A hőmérséklet és a nyomás fogalma csupán a fenomenologikus termodinamika eredményeinek felhasználásával kerül be az elméletbe. Hogy ezekben az esetekben mégis jelentős módon tudjuk továbbépíteni a tiszta fenomenologikus diszciplinákat, annak oka Hincsin szerint a következő: "Ez a tudomány a tömegjelenségeket vizsgálja, és e jelenségeknek olyan törvényszerűségeivel foglalkozik, amelyek éppen tömegjellegükből következnek és amelyek jelentős mértékben függetlenek a vizsgált tömeget alkotó egyes objektumok egyéni vonásaitól és sajátosságaitól."$^{11}$
A fizikai statisztika problémáit különösképpen a statisztikus sokaságot alkotó egyedek fizikai jellemzésének összetettsége teszi bonyolulttá. Éppen ezért a véletlen folyamatok valószínűségszámítási elméletének nagy jelentősége van a fizikai statisztikában. Ezeket a szkémákat a fizikai statisztika több területén alkalmazzák eredményesen, anélkül, hogy a szerkezeti tulajdonságokat a legkisebb mértékben is figyelembe vennék. Elég pusztán annyit tudni, hogy a fenomenologikus fizika mely fogalmai és tételei statisztikus jellegűek. Ez a szemléletmód tehát még addig sem megy el, hogy a szerkezet jellegét figyelembe vegye, csupán a statisztikus jelleg tényét használja fel.
2. A statisztikus hőelmélet alapproblémái
Álljon a vizsgált statisztikus sokaság $N$ számú egyedből pl. egy vizsgált makroszkopikus anyagi rendszer $N$ számú molekulából. A gyakorlatban $N$ igen nagy szám, nagyságrendje $10^{23}$‑hoz mérhető. A klasszikus mechanika szerint egy‑egy molekula állapotát bizonyos számú helykoordináta és impulzus‑összetevő határozza meg. Legtöbb esetben azonban elegendő csupán az egyes részecskék energiáját figyelembe venni (pl. ha a rendszer energetikailag zárt, vagyis energiája adott $E$ érték). A statisztikus hőelmélet első alapproblémája az "$E$ energia $N$ számú egyed fölötti eloszlásának meghatározása", azaz annak kiszámítása, hogy az $E$ összenergia hogyan oszlik meg az $N$ számú molekula között. Osszuk fel evégből az energiatartományt cellákra (szakaszokra), úgy, hogy egy‑egy cellában az egyedek állapota csak elhanyagolható módon különbözzék egymástól. Számozzuk meg a cellákat olyan sorrendben, hogy növekvő sorszám szerint növekvő energiaérték tartozzék hozzájuk. Az $i$‑edik cellában levő molekula energiája legyen $\varepsilon_i$. Ezáltal a $(0,\ E)$ energiaintervallumot egyértelműen szakaszokra bontottuk fel; a kölcsönhatási energia már elhanyagolható az összenergiához képest. Valami gyenge kölcsönhatást viszont mindenképpen föl kell tételeznünk, hiszen az egyes molekulák egymást befolyásolni tudják s erről számot kell adnunk. A részecskeszám és az energia megmaradási feltételének kielégítése mellett még igen sokféle eloszlás jöhet létre. Ugyanis az egyes molekulák kölcsönhatása miatt a statisztikus sokaság az örökös átrendeződés állapotában van, de az átrendeződés makroszkopikusan csak akkor észlelhető, ha az eloszlás is változik. Más szóval: bár az átrendeződés általában más és más mikroállapotba viszi a rendszert, mivel számos egymástól különböző mikroállapot ugyanazt a makroállapotot állítja elő, a makroállapotok távolról sem fognak oly sűrűn váltakozni, mint a mikroállapotok. Pl. ha két molekula egymással állapotot cserél, már más mikroállapot áll elő, de nyilvánvaló, hogy ezáltal a rendszer makroállapota nem változott meg, sőt a rendszer lényegében egyáltalán nem változott, hiszen a szerepet cserélő két molekula egymással mindenben azonos. Ily módon adott makroállapoton belül a mikroállapotok megkülönböztetése teljesen formális és fizikai szempontból teljességgel semmitmondó lenne, ha nem kellene figyelembe vennünk, hogy a molekulák kölcsönhatása következtében a rendszer az örökös átrendeződés állapotában van. így azonban a "mikroállapot" fogalmának használata mégis szükséges, mivel segítségével különböztethetjük meg a hatásos (új makroállapotokra vezető) és hatástalan (a makroállapotot változatlanul hagyó) átrendeződéseket. Több mikroállapottal megvalósuló makroállapot nagyobb valószínűséggel tudja magát fenntartani, mint az, amelyikhez kevesebb mikroállapot tartozik. Feltéve, hogy az egyes átrendeződések (mikroállapotok) kb. egyenlően valószínűek. Tehát csakis ez a "dinamikai" szemléletmód teszi indokolttá a mikroállapotok megkülönböztetését.
Ezek után térjünk rá a makroállapot valószínűségének konkrét meghatározására. Ha ismernénk minden egyes mikroállapot valószínűségét, úgy ebből rögtön kiszámíthatnánk az egyes makroállapotok valószínűségét is. Ugyanis egy bizonyos makroállapot valószínűsége nyilván egyenlő az őt megvalósító mikroállapotok valószínűségének összegével. Úgy látszik, hogy (legalábbis a részecskék gyenge kölcsönhatása esetén) jogunk van minden egyes mikroállapotot egyenlően valószínűnek feltételezni. Ezzel a feltételezéssel élve, arra a következtetésre jutunk, hogy a makroállapot valószínűsége arányos a hozzátartozó mikroállapotok számával.
A valószínűség mértékéül nemcsak a $(0,\ 1)$ intervallumba eső számokat használhatjuk; ezzel a lehetőséggel a statisztikus mechanikában is élhetünk. Mivel az elemi események (mikroállapotok) jelenleg egyenlően valószínűek, az események (makroállapotok) valószínűségeként a "kedvező" és a lehetséges esetek számának viszonyát kellene tekinteni. Azonban többek közt magát a kedvező esetek számát is tekinthetjük valószínűségi mértéknek. (E körül fog ingadozni a kedvező esetek gyakoriságának száma.) Ezt a lehetőséget a statisztikus mechanikában már kezdettől fogva felhasználják és a mikroállapotok számát tekintik az állapotvalószínűség mértékének.
További feladatunk most már összeszámlálni az adott makroállapothoz tartozó mikroállapotokat. A mondottak szerint ezek száma éppen az illető makroállapot bekövetkezésének valószínűségét adja. Vegyük tehát vizsgálat alá azt az esetet, amikor az
$$\varepsilon_1,\ \varepsilon_2,\ \varepsilon_3,\ ...,\ \varepsilon_i,\ ...,\ \varepsilon_z$$
energiájú cellában rendre
$$N_1,\ N_2,\ N_3,\ ...,\ N_i,\ ...,\ N_z$$
számú részecske van. (Lásd 14. ábra):
Idézzük fel a rendszerre vonatkozó két alapvető megszorítást: az egyik a részecskék számának, a másik a részecskék összenergiájának állandósága. A részecskeszám állandósága annyit jelent, hogy az egyes cellákban jelenlevő részecskék összlétszáma mindig $N$, azaz:
$$N_1+N_2+N_3+\thinspace ...+N_i+\thinspace ...+N_z=N=\mathrm{állandó}$$
Az összenergia állandósága pedig azt jelenti, hogy - bárhogyan oszlik is meg az energia az egyes részecskék között, mindig fennáll:
$$\varepsilon_1N_1+\varepsilon_2N_2+\varepsilon_3N_3+\thinspace ...+\varepsilon_iN_i+\thinspace ...+\varepsilon_zN_z=E=\mathrm{állandó}$$
Mivel mindegyik "cella" azonos statisztikai súllyal rendelkezik, adott $N_1,\ N_2,\ ...,\ N_i,\ ...,\ N_z$‑hez annyi mikroállapot tartozik, ahányféleképp elrendezhetők a molekulák az adott cellákban, anélkül, hogy az $N_i$ "betöltési számok" megváltoznának, azaz - a valószínűségszámitás tanúsága szerint -:
$$\frac{N!}{N_1!\ N_2!\ ...\ \! N_i!\ ...\ \! N_z!}$$
-féleképpen. Ti. az $N$ számú molekula $N!$‑féle$^{12}$ módon rendezhető el, azonban az egy cellán belüli átrendeződések - melyek száma $N_i!$ - nem változtatják meg a cserében részt vevő partnerek állapotát. Ha pontosan követni akarnánk a rendszer makroállapotainak változását, meg kellene mondanunk, milyen módon váltogatják egymást a különböző $N_i$‑k. A statisztikus tárgyalásmód szempontjából természetesen elég, ha azt ismerjük: milyen valószínűséggel cserélődnek fel a lehetséges makroállapotok. Sajnos, jelenleg erre sem tudunk válaszolni, de szerencsére nem is szükséges, a következő okokból. Az egymástól lényegesen eltérő komplexiók egymástól lényegesen eltérő makroállapotoknak felelnek meg. Ily módon a makroállapotok váltakozásával a statisztikus sokaság makroszkopikus tulajdonságai oly mértékben ingadoznak, amilyen szaporasággal a különböző $\{ Ni\}$‑kkel jellemzett állapotok követik egymást. Valójában mégis azt tapasztaljuk, hogy a makroszkopikus állapothatározók praktikusan egyáltalán nem ingadoznak. Ennek oka az, hogy túlnyomórészt bizonyos $\{ Ni\}$ elrendeződés valósul meg, a többi pedig igen ritkán és akkor is igen rövid ideig. Tehát: a különböző mikroállapotok igen gyorsan követik egymást, azonban túlnyomórészt azok a mikroállapotok szerepelnek, amelyeknél egy bizonyos $N_1,\ N_2,\ ...,\ N_i, ...=\{ Ni\}$‑hez tartozó mikroállapotok száma jóval nagyobb, mint az összes többi mikroállapotok száma.
Ha a valóságban csakugyan ez az eset valósul meg, úgy elég csupán a maximális valószínűségű állapottal törődnünk, és csak ezt kell meghatároznunk, mivel a többi szerepe gyakorlatilag teljesen elhanyagolható. Erre a feltételezésre épül Boltzmannak az az eljárása, melyet találóan a legvalószínűbb eloszlás módszerének szoktak nevezni.
Az említett módszer szerint számolva azt nyerjük, hogy $\varepsilon_i$ energiával kb.
$$N_i=a\cdot e^{\large \beta \cdot \varepsilon_{i}},\ \ \beta <0$$
számú részecske rendelkezik. Grafikusan ábrázolva:
Matematikai nehézségek miatt, sajnos, a további részletezéstől el kell tekintenünk.
Végül megjegyezzük, hogy a statisztikus mechanika jelenleg ismert módszerei csupán a makroszkopikus egyensúly tárgyalására alkalmasak. A változó állapot statisztikus mechanikája ez idő szerint még kidolgozatlan.
$\ast $
Az imént ismertetett fogalmak jobb megértése és elmélyítése céljából lássunk az áttekintés megkönnyítésére egy olyan esetet, amikor $N$ és $E$ kicsiny. A $V$ térfogat nagysága nem játszik közvetlen szerepet. Legyen bezárva $N=10$ molekula egy tetszőleges $V$ térfogatú edénybe; összes energiájuk legyen $E=20$ (lényegtelen, hogy milyen egységekben). Elégedjünk meg olyan pontossággal, hogy az energiának csupán egészre kerekített értékeit vesszük figyelembe. Így a lehetséges energia értékek
$$\varepsilon_1=1,\ \varepsilon_2=2,\ ...,\ \varepsilon_i=i,\ ...,\ \varepsilon_{11}=11$$
További egyszerűsítésként kikötjük azt is, hogy egyetlen részecske sem maradhat energia nélküli állapotban (minden részecskének van legalább $\varepsilon_1=1$ energiája), továbbá azt, hogy a fenti "cellák" mindegyike egyenlő statisztikai súllyal bír. Ez azt jelenti, hogy egy bizonyos találomra kiemelt molekula bármelyik cellában ugyanolyan valószínűséggel található. Természetesen csak az "első" részecskére vonatkoztatva és erre is csak $\varepsilon_{11}=11$‑ig. Ugyanis a részecskék egymásra gyakorolt kölcsönhatása következtében fellépő állapotváltozások nem egészen tetszőlegesek. Mint fentebb már tárgyaltuk, az összes részek száma és az összenergia változatlan, vagyis esetünkben
$$N=\sum\limits_{i=1}^{11}N_i=N_1+N_2+\thinspace ...+N_{10}=10$$
$$E=\sum\limits_{i=1}^{11}iN_i=1\ N_1+2\ N_2+\thinspace ...+10\ N_{10}=20$$
Innen rögtön leolvashatjuk, hogy egyetlen részecske legfeljebb $\varepsilon_{11}=11$ egységnyi energiával rendelkezhet. Ugyanis a maradék 9 részecske energiája minimálisan $\varepsilon_1=1$, ami összesen
$$9\ \varepsilon_{1}=9\cdot 1=9$$
energiaegységet jelent. Amihez $\varepsilon_{11}$‑et hozzáadva kapunk $E=20$ összenergiát. Tehát amennyiben például a kiemelt részecske energiája $11$, már biztosan tudhatjuk, hogy az összes többi részecske csak egy‑egy energiaegységgel rendelkezik.
A következő táblázatban feltüntetjük az $N=10$ és $E=20$ mellett lehetséges megoldásokat. Ilyen megoldás összesen 40 féle van. Figyeljük meg, hogy már ily kis $N$ és $E$ értékek mellett is, mily nagy lehet az egyes megoldásokhoz tartozó mikroállapotok száma:
$$W^j=\frac{N!}{N^j_1!\ N^j_2!\ \ ...\ }$$
($j$ a megoldás önkényesen választható sorszáma)
| $j$ | $N_1$ | $N_2$ | $N_3$ | $N_4$ | $N_5$ | $N_6$ | $N_7$ | $N_8$ | $N_9$ | $N_{10}$ | $N_{11}$ | $\sum N_i$ | $\sum iN_i$ | $W_j$ |
| 1 | 9 | 1 | 10 | 20 | 10 | |||||||||
| 2 | 8 | 1 | 1 | 10 | 20 | 90 | ||||||||
| 3 | 8 | 1 | 1 | 10 | 20 | 90 | ||||||||
| 4 | 7 | 2 | 1 | 10 | 20 | 360 | ||||||||
| 5 | 8 | 1 | 1 | 10 | 20 | 90 | ||||||||
| 6 | 7 | 1 | 1 | 1 | 10 | 20 | 720 | |||||||
| 7 | 6 | 3 | 1 | 10 | 20 | 840 | ||||||||
| 8 | 8 | 1 | 1 | 10 | 20 | 90 | ||||||||
| 9 | 7 | 1 | 1 | 1 | 10 | 20 | 720 | |||||||
| 10 | 7 | 2 | 1 | 10 | 20 | 360 | ||||||||
| 11 | 6 | 2 | 1 | 1 | 10 | 20 | 2520 | |||||||
| 12 | 5 | 4 | 1 | 10 | 20 | 1260 | ||||||||
| 13 | 8 | 2 | 10 | 20 | 45 | |||||||||
| 14 | 7 | 1 | 1 | 1 | 10 | 20 | 720 | |||||||
| 15 | 7 | 1 | 1 | 1 | 10 | 20 | 720 | |||||||
| 16 | 6 | 2 | 1 | 1 | 10 | 20 | 2520 | |||||||
| 17 | 6 | 1 | 2 | 1 | 10 | 20 | 2520 | |||||||
| 18 | 5 | 3 | 1 | 1 | 10 | 20 | 5040 | |||||||
| 19 | 4 | 5 | 1 | 10 | 20 | 1260 | ||||||||
| 20 | 7 | 1 | 2 | 10 | 20 | 360 | ||||||||
| 21 | 6 | 2 | 2 | 10 | 20 | 1260 | ||||||||
| 22 | 7 | 2 | 1 | 10 | 20 | 360 | ||||||||
| 23 | 6 | 1 | 1 | 1 | 1 | 10 | 20 | 5040 | ||||||
| 24 | 6 | 3 | 1 | 10 | 20 | 840 | ||||||||
| 25 | 5 | 3 | 1 | 1 | 10 | 20 | 5040 | |||||||
| 26 | 5 | 2 | 2 | 1 | 10 | 20 | 7560 | |||||||
| 27 | 4 | 4 | 1 | 10 | 20 | 6300 | ||||||||
| 28 | 6 | 1 | 3 | 10 | 20 | 840 | ||||||||
| 29 | 6 | 2 | 2 | 10 | 20 | 1260 | ||||||||
| 30 | 5 | 2 | 1 | 2 | 10 | 20 | 7560 | |||||||
| 31 | 4 | 4 | 2 | 10 | 20 | 3150 | ||||||||
| 32 | 5 | 1 | 3 | 1 | 10 | 20 | 5040 | |||||||
| 33 | 4 | 3 | 2 | 1 | 10 | 20 | 12600 | |||||||
| 34 | 3 | 5 | 1 | 1 | 10 | 20 | 5040 | |||||||
| 35 | 2 | 7 | 1 | 10 | 20 | 360 | ||||||||
| 36 | 5 | 5 | 10 | 20 | 252 | |||||||||
| 37 | 4 | 2 | 4 | 10 | 20 | 3150 | ||||||||
| 38 | 3 | 4 | 3 | 10 | 20 | 4200 | ||||||||
| 39 | 2 | 6 | 2 | 10 | 20 | 1260 | ||||||||
| 40 | 1 | 8 | 1 | 10 | 20 | 90 |
A táblázat szemléltető szerepének megértéséhez még egyszer felhívjuk a figyelmet a mikro- és makroállapot jelentésére.
Mikroállapot: minden egyes molekulát "személyesen" ismerünk, folyamatosan figyelve, hogy melyik részecske miként változtatja állapotát. Az egész sokaság szempontjából természetesen csak a makroállapot számít, ti. az, hogy hány részecske van egy‑egy energiaállapotban. Hogy melyek ezek a részecskék, az a makroállapot szempontjából teljesen közömbös. A makroállapotot az
$$N_1,\ N_2,\ ..., N_{11}$$
számok jelentik. Ha ezenkívül azt is tudni akarjuk, hogy melyik rész milyen állapotban van, ill. hogy adott $N_1,\ N_2,\ ..., N_{11}$ makroállapot hányféle mikroállapottal valósítható meg, meg kell keresnünk minden lehetséges elrendeződést. Az adott egyetlen makroállapothoz tartozó mikroállapotok (tehát lehetséges elrendeződések!) száma éppen a $W^j$. A táblázat egyik oszlopa ezt az adatot is tartalmazza.
A táblázat tanulmányozása valóban meglepő tényekre tereli rá figyelmünket. A maximális valószínűségű állapothoz tartozó mikroállapotok száma $12\ 600$. Gondoljuk el, mily nagy számot kapunk akkor, ha $N$ és $E$ már magában is áttekinthetetlenül nagy szám. Sorra véve az összes makroállapotokat és összeadva a hozzájuk tartozó mikroállapotok számát, az összes lehetőségek számát nyerjük
$$W=\mathit{\Sigma }\ W^j$$
Mivel a $j$‑edik makroállapotot megvalósító kedvező esetek száma $W^j$ és $W$ az összes lehetőségek száma, minden lehetőség egyenlően valószínű lévén, a $j$‑edik makroállapot bekövetkezésének valószínűsége:
$$w^j=\frac{\ \ W^j}{W}$$
A táblázat alapján ezek is kiszámíthatók, s ismeretükben az átlagos betöltési számot is megkaphatjuk
$$\overline{N_i}=\mathit{\Sigma }\ N^j_1\frac{\ \ W^j}{W}$$
Ha a számítást elvégezzük, azt tapasztaljuk, hogy az átlagos betöltési számok valóban igen közel esnek a legvalószínűbb eloszlás betöltési számaihoz.
Pontosan a fenti számadatokkal rendelkező, de egészen más tartalmú problémákra is alkalmazhatjuk meggondolásainkat. $N$ és $E$ kicsiny lévén, gondoljunk például erre az esetre: $N=10$ ember hajótörést szenved. Szerencsés megmenekülésük után egy megélhetésük számára mindenképp kielégítő $V$ területű szigetre kerülnek. A kis embercsoportban kialakuló kereskedelmi életben pénzként $E=20\ \mathrm{db}$ különleges, még a hajóról magukkal hozott érmét használnak. (Az adott viszonyok közt ezeket nem lehet hamisítani.) Feltéve, hogy a leegyszerűsített viszonyok közt egyik személy sincs előnyben a többivel szemben, formailag az előbb tárgyalt problémával állunk szemben. $N$ és $E$ állandó volta mellett 40 féle eloszlást (ti. a 20 pénzdarabnak a 10 ember közötti 40 féle eloszlását) kell figyelembe vennünk. Ha az adásvételi folyamatok elég gyorsan követik egymást (élénk a "pénz" vándorlása), úgy az elég hosszú időn keresztül végzett megfigyelés eredményét az átlagos betöltési számokkal, ill. az ezektől igen kevéssé különböző legvalószínűbb állapot betöltési számaival jellemezhetjük. Átlagban tehát úgy oszlik el a pénz, hogy négy embernek egy‑egy, három embernek két‑két, két embernek három‑három és egy embernek négy érméje van. (E példára az entrópia statisztikus értelmezése kapcsán még visszatérünk.)
3. Entrópia és állapotvalószínűség
A továbbiakban csupán annyit tételezünk fel az $\{Ni \}$ makroállapot valószínűségéről, hogy egyáltalán létezik. Aszerint, hogy milyen szkémával dolgozunk, kifejezését más és más formában nyerjük. Az állapotvalószínűségnek ugyanis van valami minden speciális formától független, minden statisztikai szkémára érvényes fenomenologikus jelentése. Boltzmann mutatott rá arra a körülményre, hogy a $w$ állapotvalószínűségnek az $S$ entrópia monoton növekvő függvénye.
$$S=f(w)$$
Erre utal már az a tény is, hogy zárt rendszer entrópiája minden folyamatnál növekszik; ugyanakkor a rendszer a kisebb valószínűségi állapotból a nagyobb valószínűségű állapot elérésére törekszik. Tehát entrópia és valószínűség párhuzamosan nőnek.
Ebből a feltételezésből kiindulva a függvénykapcsolat konkrétan is megállapítható, figyelembe véve az entrópia additivitására és a valószínűségek szorzására vonatkozó tételeket. Tekintsük két termikusan gyengén kapcsolt rendszert. A termikus kapcsolás az entrópia additivitásának szükséges feltétele, a kapcsolás gyenge voltát pedig azért tételezzük fel, mert így a két rendszert jó közelítéssel mégis egymástól függetlennek tekinthetjük és a valószínűségek szorzástételét alkalmazhatjuk esetünkben. Jelöljük a két rendszer entrópiáját rendre $S_1$ és $S_2$‑vel, állapotvalószínűségét pedig $w_1$, ill. $w_2$‑vel. Az előbbi feltételek mellett az egyesített rendszer entrópiáját - és $w$ állapotvalószínűségét a következő módon nyerjük
$$S=S_1+S_2$$
$$w=w_1\cdot w_2$$
Így a Boltzmann‑féle feltétel alapján
$$S=f(w)=S_1+S_2=f(w_1)+f(w_2)$$
röviden
$$f(w_1\cdot w_2)=f(w_1)+f(w_2)$$
Az $f(w)$ függvénykapcsolat ebből a függvényegyenletből már megállapítható: az itt szereplő függvénykapcsolatnak éppen a logaritmus függvény tesz eleget.$^{13}$
$$S=k\log{w}$$
Eszerint az entrópia az állapotvalószínűség logaritmusával arányos.
Az összefüggésben szereplő $k$ arányossági tényező univerzális állandó, tehát értékét elegendő egyetlen konkrét esetben meghatározni (értéke $1,37\cdot 10^{-18}\ \mathrm{erg/fok/})$. Mivel a $\log{w}$ dimenziónélküli szám, $k$ dimenziójának entrópiajellegűnek kell lennie.
Figyelembe véve az előző pontban tett megállapításainkat, hogy ti. az állapotvalószinűség:
$$w=\frac{N!}{N_1!\ N_2!\ ...\ \! N_i!\ ...\ }$$
$N_i=\alpha \cdot e^{\large \beta\cdot \varepsilon_i}$ ($\alpha $, $\beta $ adott állapotban = állandó), továbbá azt a matematikai tényt, hogy igen jó közelítéssel
$$N\simeq \left(\frac{N}{e}\right)^N$$
a legvalószínűbb eloszláshoz tartozó entrópia már könnyen kiszámítható. Induljunk ki az előbb megismert
$$S=k\log{w}$$
alapegyenletből, ahol a fentiek szerint
$$w=\frac{N!}{N^j_1!\ N^j_2!\ \ ...\ }\simeq \frac{\displaystyle \left(\frac{N}{e}\right)^N}{\displaystyle \left(\frac{\ N_1}{e}\right)^{N_1}\cdot \displaystyle \left(\frac{\ N_2}{e}\right)^{N_2}\ ...\ } $$
$$=\frac{\displaystyle \left(\frac{1}{e}\right)^N}{\displaystyle \left(\frac{1}{e}\right)^{N_1+N_2+...}\ } \frac{N^N}{\ N_1^{N_1}\cdot N_2^{N_2}\ ... \ }$$
Az első tényező osztójának kitevőjében $\sum\limits_{(i)}N_i=N$, tehát e tényező éppen egységnyi;
$$w=\frac{N^N}{N_1^{N_1}\cdot N_2^{N_2}\ ... \ }$$
Helyettesítsük ezt az $S$ kifejezésbe, úgy
$$S=k\left(N\log{N}-\sum N_i \log{N_i}\right)$$
amit még át is alakíthatunk alkalmas módon. Ti. a $\log{N}$ együtthatója így írható
$$N=\sum N_i$$
tehát
$$S=-kN\sum \frac{\ N_i}{N} \log{\frac{\ N_i}{N}}$$
Az itt szereplő $N_i$‑k a maximális valószínűségű állapothoz tartozó betöltési számok, míg a
$$p_1=\frac{\ N_i}{N}$$
mennyiségek az ún. relatív gyakoriságok. Ez utóbbiak egyúttal az $i$‑edik cellában való találat valószínűségei is. Ily módon az entrópia:
$$S=-kN\sum\limits_{(i)} p_i \log{p_i}$$
Alkalmazzuk ezt a képletet a legvalószínűbb állapothoz tartozó eloszlásra, az előző pont végén tárgyalt példa esetében. Láttuk, hogy
$$N_1= 4,\ N_2=3,\ N_3=2,\ N_4=1,\ N_5=\ ...\ \! =$$
$$=N_{11}=0;\ N=\sum N_i=10$$
Tehát
$$p_1=\frac{4}{10},\ p_2=\frac{3}{10},\ p_3=\frac{2}{10},\ p_4=\frac{1}{10},\ p_5=$$
$$=\ ...\ \! =p_{11}=0$$
és így a legvalószínűbb eloszlás entrópiája:
$$S=-k\cdot 10\left(\frac{4}{10}\cdot \log{\frac{4}{10}+\frac{3}{10}}\cdot \log{\frac{3}{10}+\frac{2}{10}}\cdot \log{\frac{2}{10}+\frac{1}{10}}\cdot \log{\frac{1}{10}}\right)$$
Mivel mindez nemcsak molekulákra és energiára, hanem pl. bizonyos pénzösszegnek adott számú ember közt való eloszlására is alkalmazható, természetes, hogy az entrópia fogalmának szintén értelme van az adatok utóbbi jelentése mellett is. Nem fogunk tehát semmi meglepőt találni abban, hogy az információelmélet az entrópia fogalmát mily nagy területre tudta kiterjeszteni. A következőkben hasznos lesz az entrópia információelméleti általánosításával is megismerkedni.
4. Hőelmélet és információelmélet
Az információelmélet eredetét tekintve két forrást jelölhetünk meg: a híradástechnikát és a statisztikus termodinamikát (illetőleg általánosabban a statisztikus fizikát). Az új elmélet megalkotásának igénye a híradástechnika részéről merült fel, a statisztikus fizika viszont az alapvető fogalmakat adta. Milyen közös vonások révén kerülhetett a híradástechnika és a statisztikus fizika oly közel egymáshoz, hogy bizonyos problémákat azonos általános nézőpontból lehetett vizsgálni? A közös "nevező" nyilvánvalóan a valószínűségszámítás, mely mindkét tudomány formanyelvét alkotja. Mindez a kész elmélet ismeretében már világos, de tudjuk, hogy az új elmélet gondolata lassú fejlődési folyamat eredményeként született meg.
Jelenlegi feladatunk csupán bizonyos fizikai problémák információelméleti szempontok alapján történő boncolgatása, így az információelmélet kialakulásához vezető tényezők közül csak a fizikai vonatkozásúakkal foglalkozunk. A fizikának egyrészt sok olyan régebben ismert elvi érdekességű problémája van, melynek hiánytalan megoldása csak az információelmélet segítségével végezhető el, másrészt: sok olyan alapvető elvi‑fizikai fogalom és e fogalmakra vonatkozó tétel ismeretes, mely nélkül az új elmélet aligha születhetett volna meg. Tájékozódásul tekintsük át röviden a fizika történetének idevágó legfontosabb mozzanatait.
A döntő lépést Clausius tette meg az entrópiafogalom felismerésével. Boltzmann ennek az eredetileg fenomenologikus alapon született fogalomnak a statisztikus értelmezését végezte el. Míg az entrópia fenomenologikus meghatározása sok kimondottan termodinamikai jellegű speciális tartalmi jeggyel rendelkezik, a Boltzmann‑féle értelmezésből már világosan látszik, hogy a tömegjelenségeket igen általánosan jellemző fogalom birtokába jutottunk.
Emlékezetbe idézve az entrópia Boltzmann‑féle statisztikus értelmezését látjuk, hogy ebben csupán két meghatározó tényező szerepel. Boltzmann megállapítása így szól: az entrópia a termodinamikai állapot valószínűségének logaritmusával arányos.
$$S=k\log{w}$$
Az első szembetűnő mozzanat a valószínűség; a második az, hogy a termodinamikai állapot valószínűségéről van szó. Innen már csak egy lépést kell tennünk, hogy eljussunk az általános fogalomig. Hagyjuk el a "termodinamikai" jelzőt, és már előttünk is áll valamennyi tömegjelenség közös jellemzőjének meghatározása: az állapot valószínűségének logaritmusa. Boltzmann tétele tehát egyrészt közelebb juttatta a tudományt az általános entrópia‑fogalom felismeréséhez, másrészt utat nyitott információelméleti jellegű termodinamikai és statisztikus fizikai problémák felvetéséhez.
Csupán felsorolásszerűen foglaljuk össze a fejlődést jelentő problémákat és eredményeket. Már kezdetben felmerült a kérdés: milyen mélyebben fekvő alapokra lehet visszavezetni az irreverzibilis folyamatoknál föllépő entrópianövekedést? Bár ma sem ismerünk teljesen kielégítő választ, születtek részleteredmények, amelyek kétségkívül pozitív irányú haladást jelentenek. Boltzmann bizonyítást adott az irreverzibilis entrópianövekedésre, de kiderült, hogy ez a bizonyítás sok vonatkozásban nem fogadható el. Poincaré és Zermelo ugyanis kimutatta, hogy elég nagy idő elteltével minden zárt mechanikai rendszer visszatér eredeti állapotának közelébe. Mivel pedig végső fokon az összefüggő anyag is a mechanika törvényeinek engedelmeskedő molekulákból áll, a termodinamikai testek "mikroállapotai" periodikusan újra és újra ismétlődnek, amivel pedig a "makroállapot" és így az entrópia ismétlődése is együtt jár. ("Visszatérési tétel", "Wiederkehrsatz".) Ezzel rokonjelentésű Loschmidt "megfordíthatósági tétele" ("Umkehrsatz"), mely szerint a termodinamikai rendszer részecskéinek impulzusát ellenkezőjére változtatva, két állapot közti átmenet mindkét irányban végbemehet. Úgy látszik, hogy ezek a megállapítások gyökeresen ellentmondanak az irreverzibilitás tényének. Az ellentmondás feloldására irányuló vizsgálatok egyik, számunkra különösen figyelemre méltó eredménye éppen bizonyos információelméleti vonatkozások tudatosulása volt: az entrópia az állapotra vonatkozó tudatlanságunk mértéke. Bár ez a megállapítás ebben a formában még lényeges kiegészítésre szorul, mégis jelentős, mert újabb előrehaladást jelentett az általános entrópiafogalom felismerése felé.
A kvantumelmélet valószínűségszámítási értelmezése szintén igen sok olyan problémát vetett fel, amelyek megoldása egyúttal az információelmélet kialakulásának útját is egyengette. Itt elsősorban Neumann Jánosnak a kvantummechanikai méréselméletre vonatkozó vizsgálatait kell megemlítenünk. Ismeretes a kvantumelmélet ún. "spontán" és "mérési" folyamatainak egymással való szembenállása, mely igen sok paradox következtetés forrása. Mi módon lehet a mérés által történő zavaró hatást és a megfigyelés puszta tényéből adódó "tiszta" információt szétválasztani egymástól? E kérdés megválaszolásának egyik jelentős mozzanata a kvantumelméleti entrópiafogalom megalkotása. Neumann a kvantumelméleti entrópia meghatározásakor még nem alkalmazhatott tudatos információelméleti szemléletet, így - Szilárd Leó útmutatására - termodinamikai analógiák felkeresésével kerülte ki a nehézséget. A kvantumelméletben vált először ismertté az a tény is, hogy két, egymással valószínűségi függésben levő fizikai mennyiség egyidejű mérhetőségének korlátai vannak. Az idézett megállapítás Heinsenberg‑féle bizonytalansági reláció néven ismeretes. Később R. Fürth bebizonyította, hogy formailag teljesen hasonló bizonytalansági reláció áll fenn a Brown‑részecskék mozgására vonatkozóan is.
5. Az "információ" mennyiségi jellemzésének lehetőségei
A fizika és általában a természettudomány módszere szerint a kezdetben kvalitatíve megsejtett tulajdonságokat mielőbb kvantitatíve is jellemezni kell. Jellegzetes fizikai ill. fizikokémiai példaként a kémiai affinitás fogalmára utalunk. A kémiai affinitás bizonyos kémiai anyagok kémiai egyesülésre való törekvését kifejező tulajdonsága. Már régen felismerték, hogy az anyagok e tulajdonságát feltétlenül figyelembe kell venni, de pontos értelmezését illetően sötétben tapogatóztak. Több javaslat merült fel, míg végre megszületett a találó fogalomalkotás. Az említett példában csakúgy, mint a hasonló esetekben, főként az okozza a nehézséget, hogy kezdetben csak homályosan körvonalazódnak az igények, inkább sejtik, mint tudják, mit szeretnének. így bizonyos tisztulási folyamat után sikerül csak célt érni.
Fentiek előrebocsátásával azt akarjuk már kezdetben érzékeltetni, hogy az "információ" kezdeti, kvalitatív fogalma alapján az egzakt fogalom kialakulása hasonlóképpen történt. Ha az "információ" mennyiségi értelmezését a kellő egzaktságon túlmenően a szükséges pedagógiai tapintattal akarjuk elvégezni, úgy e körülményeket nem hagyhatjuk figyelmen kívül.
A hírforrásból nyerhető "hír"‑ek, "információ"‑k alapvető jellegzetessége az, hogy nem tudjuk előre: milyen értesülésekhez fogunk jutni. A hír és a hír meglepő volta elválaszthatatlanul összetartoznak: a jel, melyről biztosan tudjuk előre, hogy micsoda, nem hír. Másként kifejezve: a hírt az jellemzi, hogy megszerzését megelőzően bizonytalanok vagyunk tartalmáról. Mivel általános értelemben hírekkel nemcsak a híradástechnika, hanem a "tiszta" tudományok - köztük a fizika - is foglalkozik, általános természettudományos igénynek tekinthetjük a hír meglepő voltának, ill. bizonytalanságának pontos, számszerű jellemzését. Ezt kimondva, egy pillanatra meghökkenünk, hiszen csak sejtjük, mit akarunk, nem vagyunk birtokában pontosan megfogalmazott feltételeknek, amelyek egyértelmű fogalomalkotáshoz vezetnek. A "meglepő‑mivolt", ill. a "bizonytalanság" nem jelent elegendő megszorítást.
Mindenekelőtt nézzük meg milyen természetű követelményeket kell teljesítenünk egy kvalitatíve értelmezett fogalom kvantitatív és egyértelmű jellemzése során. Carnap szerint öt követelményt kell rögzítenünk. Ezek:
- A mennyiség zéruspontja
- egysége
- egyenlőség‑definíciója
- kisebb‑nagyobb vonatkozása
- skálája
Eltekintve azoktól az esetektől, midőn egy‑egy esetben a természet által kitüntetett zéruspont, ill. egység létezik, az 1. és 2.‑beli megszorítások nagymértékben önkényes megállapodással adhatók meg. A 3. és a 4. követelmény viszont mindig a vizsgált probléma természetéből adódik, így jelen esetben is különösen erre kell gondot fordítanunk. Végül a skála kérdése közbenső helyet foglal el, ti. nem mindig van egyetlenként kitüntetett, ún. "abszolút skála". A kétségkívül legegzaktabb természettudományban, a fizikában is gyakran csupán célszerűségi szempontok alapján született konvenció az, amelynek alapján egy‑egy mennyiség skáláját rögzítjük. A skála‑formát csak akkor tekinthetjük természeti törvénynek, ha törvényszerű transzformációs követelményeknek tesz eleget.
Visszatérve most már fentebb felvetett problémánkra, igényeinket úgy kell megfogalmazni, hogy az 1‑5 követelmények mindegyikét egyértelműen kielégítsük. Mivel első támpontunk - a "meglepő‑mivolt" ill. "bizonytalanság"‑jelentése - csak a valószínűségszámítás keretében találhat egzakt megfogalmazásra, a megoldást a valószínűségszámítás fogalomrendszerében kell keresnünk. A tömegjelenségek bármely típusának valószínűségi elmélete mindig azon a feltételezésen alapul, hogy az elemi (sőt: véletlen) események meghatározott, tehát ismert rendszerével van dolgunk. Ezt a feltételezést az információelméletben is meg kell tartanunk, hiszen az olyan hír, amelyiknek természetéről nem tudunk semmit, értelmetlen és így érdektelen számunkra. Tekintsük tehát egy hírforrás meghatározott és véges számú hírből álló hírkészletét$^{14}$ mint az
$$A_1,\ A_2,\ ...,\ A_n$$
véletlen események teljes rendszerét; az $A_1,\ A_2,\ ...,\ A_n$ jelzésű események bekövetkezési valószínűsége rendre:
$$p_1,\ p_2,\ ...,\ p_n$$
Nem nehéz észrevennünk, hogy a $p_1$ valószínűségek megadásával már meg is oldottuk feladatunkat. Esetleg azt kellene még figyelembe vennünk, hogy az $A_1$ események számszerűen milyen értékkel bírnak. Nyilvánvaló ugyanis, hogy a $\xi $ valószínűségi változó
$$(A_1,\ A_2,\ ...,\ A_n)$$
$$x_1,\ x_2,\ ...,\ x_n$$
$$p_1,\ p_2,\ ...,\ p_n;\ \sum p_i=1$$
értékkészletének és valószínűségi eloszlásának birtokában maximális mértékben jellemeztük a hírforrásból nyerhető hírek bizonytalanságát. Az olyan esetekben, midőn $n$ kicsiny és így a fenti értékkészletek jól áttekinthetők, nemcsak elvileg, de gyakorlatilag is használható egyszerűen maga a valószínűségi mező. Példaként nézzük a pénz- ill. a kockadobás problémáját. Egyikben két, a másikban hat esettel van dolgunk. Az az ismeret, hogy a "fej" és "írás" - mint lehetséges hír - bekövetkezése egyaránt $\displaystyle \frac{1}{2}$ valószínűséggel történhet (szabályos pénzdarab), igen találóan jellemzi a hírforrás bizonytalanságát. Ha a pénzdarab nem szabályos, úgy általában a
$$\begin{array}{cc} \mathrm{"\! fej\! "} & \mathrm{"\! írás\! "} \\ p & \! 1-p \end{array}$$
szkéma játsza ugyanezt a szerepet. Kockadobásnál (mindjárt az általánosabb esetet tekintve), az
$$x_1,\ x_2,\ x_3,\ x_4,\ x_5,\ x_6$$
$$p_1,\ p_2,\ p_3,\ p_4,\ p_5,\ p_6;\ \sum\limits_{i=1}^{6}p_1=1$$
szkéma még szintén jól áttekinthető (egyszerre felfogható a benne foglalt jellemzés), így a hírforrás híreinek bizonytalanságáról is pontos képünk van. Eddig nem említett, új vonatkozású probléma merül azonban fel akkor, ha $n$ igen nagy. A valószínűségi mező elvileg most is éppoly jó képet ad a hírforrás bizonytalanságáról, mint előbb, de az a baj, hogy egyszerre csak egy‑egy kis részletet tudunk áttekinteni, elveszünk a részletekben. A mondottakat figyelembe véve, kézenfekvőnek látszik a meglepő‑mivoltot a szórás fogalmával azonosítani. Ha azonban figyelembe vesszük, hogy a szórás megadása két különböző formában lehetséges, látjuk: mily döntő mértékben befolyásolja a kapott számértéket az önkényes megállapodás. A tanulságot általános szempontként mondhatjuk ki: a szórás mellett a bizonytalanságnak olyan másik mértékét is meg kell adnunk, amelyik csak a valószínűségi eloszlástól függ:
$$I=f(p_1,\ p_2,\ ...,\ p_n)$$
Az ilyen mérőszám nyilvánvalóan minden valószínűségi mezőn értelmezhető, tehát alkalmazási területe a lehető legszélesebb. Előrebocsátjuk, hogy a bizonytalanság mértékéül szolgáló $I$ információmennyiség egyértelmű meghatározásához nem tudunk elegendő "természetes" szempontot találni, így végső fokon elvileg több lehetőség közt választhatunk. Az a körülmény, hogy a történeti fejlődés kapcsán a választás a termodinamikai entrópia formai általánosítására esett, nyilvánvalóan nem logikai szükségszerűségből történt. Mindezt szükségesnek tartottuk elmondani, mert gyakran találkozunk az információmennyiségnek olyan értelmezésével, mely szükségszerűnek igyekszik feltüntetni az entrópiával való azonosságot.
Tegyük fel, hogy valamilyen - többé-kevésbbé természetes - szempontok alapján meghatároztuk az $I=f(p_1,\ p_2,\ ...)$ információmennyiség formáját. Tekintsünk most már egy olyan $F(x)$ függvényt, mely
- $x$-ben folytonos és monoton
- $F(0)=0$
- $F(1)=1$
Mivel a szóban forgó $F(x)$ függvények választási lehetősége végtelen,$^{15}$ ez a körülmény is mutatja, mennyire nem lehet tisztán "természetes" szempontok alapján rögzíteni az $I$ formáját. Ily módon sem tudományos, sem didaktikai szempontból nem vétkezünk, ha a statisztikus termodinamikai entrópia szemléletes jelentésére hivatkozva az információmennyiséget formailag az entrópiával azonosítjuk:
$$I=S=-K\sum p_i \log{p_i},\ K=\mathrm{állandó}$$
Az értelmezésből következik, hogy $S$ mindig pozitív. Végül pedig annyit jegyzünk meg, hogy a $K$ állandó értéke az egység megválasztásától függ és, hogy egy lehetséges additív állandót eleve úgy választottunk, hogy $S$ minimális értéke zérus legyen.
Az információmennyiség, ill. entrópia elnevezés mellett az irodalomban más elnevezésekkel is találkozunk. Gyakran használják az $N=-S$-re a negentrópia kifejezést: a magyar szaknyelvben egyes helyeken a "hírtartalom" elnevezés is szerepel, ami elég találó megjelölés. Talán nem lesz hiábavaló, ha végül még azzal a kérdéssel is foglalkozunk, hogy az entrópia szó használata mennyire jogosult a termodinamikától teljesen független tárgykörben. Azt hiszem, hogy nem adhatunk igazat azoknak, akik a tárgykör lényeges különbségére hivatkozva, csupán teljesen külsődleges analógiának minősítik az információmennyiség és a termodinamikai entrópia kapcsolatát és így még az entrópia szó használata ellen is tiltakoznak. A különböző tudományok területén gyakran találkozunk olyan fogalmakkal, melyek ugyanazon elnevezéssel hol ilyen, hol olyan tartalom formái. Példaként a "sűrűség" fogalmára hivatkozunk. Van népsűrűség, anyagsűrűség, energiasűrűség stb; mind más‑más tartalmú fogalmat jelöl, de "formai" jelentésük azonos. Az egészen triviális "szám" fogalmat csak éppen megemlítjük. Hasonló a helyzet az entrópiával is. A termodinamikai, a kvantumelméleti, az információelméleti entrópia más és más ugyan, de a megfelelő résztudományokban viselt funkciójukat tekintve formailag azonosak. Az a körülmény pedig, hogy az "absztrakt" entrópiafogalom a valószínűségszámítás keretében értelmezhető, még mélyebbé teszi a különböző fajta entrópiák kapcsolatát, ti. a valószínűségszámítás átmenetet képez a matematika elvontabb ágai és a természettudományok között. A valószínűségszámítás a tömegjelenségek általános modelljével foglalkozik, szemléletmódja minden konkrét tömegjelenségre jól alkalmazható. Ebből viszont az következik, hogy a matematikai információelmélet szemléletmódja minden olyan esetben termékenyen alkalmazható, ahol az entrópia fogalma szerepet játszik.
A múlt században Maxwell tette fel a kővetkező kérdést: túlteheti‑e magát az entrópiatörvény korlátain egy olyan megfigyelő, aki minden egyes molekula állapotát egyidejűleg mérni tudja és állapotváltozásukat pontosan követni képes? (Maxwell‑féle démon.) Tekintsünk ui. két gáz halmazállapotú testet, melyek egyenlő hőmérsékletűek, és melyeket tolóajtóval ellátott fal választ el egymástól. A Maxwell‑démon, ismervén az ajtó felé közeledő molekulák helyzetét és sebességét, az ajtó pillanatnyi félrehúzásával egyik edényből a másikba engedhet át egyes molekulákat. Az ajtó megfelelő nyitogatásával elérheti például, hogy az igen nagy sebességű molekulák az egyik, az igen kis sebességű molekulák a másik edénybe "terelődnek". Az egyensúly nyilván megbomlik: az egyik edényben levő gáz magasabb hőmérsékletű lesz, a másik lehűl. A mondott folyamat éppen ellentéte a hőmérséklet kiegyenlítődésnek, vagyis entrópiacsökkenéssel jár, ellentétben a második főtétellel. Ha eltekintünk attól a szükségszerűségtől, hogy a megfigyelő mindig molekuláris szerkezetű (tehát a termodinamikai káosz állapotában levő) mérőeszközök segítségével mér, úgy valóban "démon"‑nal állunk szemben, akire a második főtétel korlátozásai nem vonatkoznak. Termodinamikai testeket használva mérőeszközökként, természetesen a Maxwell‑démon sem tud kompenzálatlan entrópiacsökkenést előidézni. Röviden ez a lényege azon gondolatmenetek egyikének, melyekkel a Maxwell‑démon‑probléma során felmerült elvi nehézséget manapság elhárítják.
Remélem, az olvasó egy pillanatra sem gondol arra, hogy Maxwell valóban gondolt egy ilyen "démon" létezésére. Csupán arról van szó, hogy a Maxwell‑démon által "végrehajtott" gondolati kísérlet segítségével mélyebben belelátunk az entrópiafogalom statisztikus jellegébe. Egyébként amilyen merész a felvetett ötlet, olyan szűk látókörű az ismertetett cáfolat. Ha démon, hát legyen démon, menjünk bele a játékba. Ennek ellenére alapvető tévedés, hogy - akár ily módon is - a második főtétel érvényét veszti. A Maxwell‑démon elejétől fogva mindent (mérni) tud, így az ő rendszerében az entrópia elejétől fogva zérus és további kísérletei során is zérus marad. Entrópiacsökkenésről tehát szó sincs. Mindez rendben volna, de mit szóljon az a közönséges megfigyelő, aki csupán annyit észlel az egész folyamatból, hogy két egyenlő hőmérsékletű gáz különböző hőmérsékletűvé vált? Nyilván nem szellemek játékára fog gondolni, hanem arra, hogy a hőmérséklet‑különbség valamilyen eddig előtte ismeretlen intenzitás‑mennyiség kiegyenlítődése által jött létre. A démon nagyobb tudása valóban felfogható így, miáltal a második főtétel minden szempontból érvényben marad. Nincs abban semmi meglepő, hogy ugyanazon hírforrás entrópiája különböző megfigyelők számára különbözőnek adódik. Ha az egyik megfigyelő nagyobb tudású a másiknál (s így a nyerhető hírekről előre többet tud, mint a másik), kisebb entrópiát tulajdonít a hírforrásnak. A démon és a közönséges megfigyelő esetében is pontosan ez a helyzet... Amennyire a Maxwell‑démon játékos kitalálás csupán, ugyanolyan komolyan kell venni azt a lehetőséget, hogy a tudomány fejlődésével többet tudhatunk előre a termodinamikai rendszerekről, ami a jelenlegi helyzet szempontjából kompenzálatlan entrópiacsökkenést jelent. Éppen az utóbb tárgyalt kérdéssel kapcsolatban hadd említsem meg, hogy a nagyobb sebességű molekuláknak a relativisztikus tömegnövekedés következtében nagyobb a tömege. A kis- és nagysebességű molekulák szétválasztására (elvben) ez a körülmény újabb lehetőségeket ad. Ez és még sok eddig nem is sejtett tény talán lehetővé teszi majd, hogy bizonyos folyamatok jelenlegi optimális hatásfokát a második főtétel megsértése nélkül javítani lehessen...
Foglalkozzunk a továbbiakban azzal a kérdéssel, hogy valamely termodinamikai rendszer egy‑egy molekulája állapotának mérése során miként változik az entrópia. Egyszerűség kedvéért jelöljük most a teljes állapotot egyetlen indexszel. (Az impulzus szerinti és a térbeli eloszlás egymástól való megkülönböztetése ezúttal nem fontos számunkra). Így az $N$ számú molekulából álló rendszer entrópiája:
$$S=-kN\sum\limits_{(i)}p_i \log{p_i}$$
Mármost egyetlen molekula állapotát megmérve (vagyis meghatározva az állapottérnek azt a $j=1$ jelzésű tartományát, amelyikbe a részecske beletartozik), két lehetőség adódik. Először: a megfigyelőnek olyan ideális műszerei vannak, amelyekkel valóban abszolút pontosan lehet mérni. Ekkor a mérés során szerzett ismeret következtében, a kiszemelt részecske tartózkodási valószínűsége: egy,
$$\overline{p_i}=1$$
a többi valószínűség: zérus,
$$\overline{p_i}=1,\ \ i\neq j$$
Így a megfelelő entrópia is zérus.
$$-k\sum\limits_{(i)} \overline{p_i} \log{\overline{p_i}}$$
Ennyi hiányozni fog az eredeti entrópiaértékből. A maradék tehát
$$-k(N-1)\sum\limits_{(i)}p_i \log{p_i}$$
A mérés folytán fellépő entrópiacsökkenés:
$$-k\sum p_i \log{p_i}$$
Mint mondottuk, ez annak a következménye, hogy a megfigyelő ideális műszerei más fizikai feltételt szabnak az eredeti feltételekhez képest. Most sem arról van szó tehát, hogy pusztán a szubjektíve fennálló tudás változtatja meg az entrópiát. Az entrópiacsökkenés oka a pontosabban működő, több adatot regisztrálni tudó műszer létezésében keresendő, ami pedig nagyon is objektív körülmény. Hiába gondolunk mi arra, hogy az egyes molekuláknak pontosan meghatározott állapotuk van, ettől az entrópia még nem lesz kisebb. Ellenben, ha eddigi műszereinknél pontosabb műszerünk van, úgy ezen eszköz által realizálódó fizikai feltételek mellett objektíve kisebb az entrópia. Mindebből az derül ki, hogy az entrópia nemcsak magának a "hírforrásnak" az adata, hanem a hírforrás és a megfigyelési eszközök által szabott fizikai feltételek együttesének jellemzője.
Második lehetőség: a mérőműszerek maguk is molekuláris szerkezetűek, így a megfigyelt molekula pontos viselkedését megint csak nem tudjuk regisztrálni. Ennek megfelelően pontos és megbízható állapotmeghatározás sem lehetséges, csupán statisztikus kijelentést tehetünk a molekula állapotáról. E statisztikus kijelentés viszont éppen abban áll, hogy ismételten regisztrálja a $p_1,\ p_2,\ ...,\ p_i,\ ...$ valószínűségi eloszlást, vagyis nem tudtunk meg többet a rendszerről: a mérés az entrópia értékét nem csökkenti. Ez érthető is, hiszen az objektív fizikai feltételek nem változnak.
A fentiekből fontos tanulságot vonhatunk le. Gyakran lehet hallani ilyen kijelentéseket: az entrópia tudatlanságunk mértéke. Ez semmiképp sem igaz a tudás szubjektív vonatkozásában: az entrópia annak a határozatlanságnak a mértéke, amelyet a mérőműszerek objektív pontatlansága okoz. Ez az objektív pontatlanság természetesen függhet a tudományos megismerés helyzetétől: a törvények pontosabb ismerete ugyanis pontosabb mérőműszerek készítését teszi lehetővé.
A statisztikus elméleteknek bizonyos jellemzők várható értékének meghatározása mellett az is feladata, hogy a szükségszerűen fellépő ingadozásokról is számot adjon. Így az entrópianövekedés (másképpen: kiegyenlítődésre való törekvés) tételével kapcsolatban figyelembe kell vennünk, hogy ez csupán átlagban érvényes: a statisztikus ingadozások következtében kis valószínűséggel fellép spontán entrópiacsökkenés is. Minél kisebbek a test méretei, annál gyakoribbak az ingadozások; nagyméretű testek esetében igen hosszú időtartam szükséges számottevő spontán entrópiacsökkenés bekövetkezésére. E problémakör természetesen nemcsak az entrópia‑ingadozások számbavétele szempontjából érdekes. Különösen fontos R. Fürthnek az az 1925‑ből származó felismerése, hogy a kolloid-részecskék ún. Brown‑féle mozgásával kapcsolatbán fennáll egy bizonytalansági reláció. Feltűnő a Fürth‑féle reláció nagymértékű formai hasonlósága a Heisenberg‑féle bizonytalansági relációhoz.
A Heisenberg‑féle bizonytalansági reláció szerint egy elemi rész (pl. elektron) helyének és sebességének egyidejű mérése csak oly pontossággal lehetséges, hogy a mérési hibák szorzata bizonyos korlát fölött marad. Jelöljük a hely mérésének hibáját $\Delta x$‑el, a sebességét $\Delta v$‑vel, akkor a Heisenberg‑reláció szerint
$$\Delta x\cdot \Delta v>\frac{h}{4\pi m}$$
ahol $h$ az ún. Planck‑féle állandó, $m$ a részecske tömege. A kolloid‑részecskékre vonatkozó Fürth‑féle reláció a következő:
$$\Delta x\cdot \Delta v>D$$
ahol $\Delta x$ és $\Delta v$ jelentése az előbbivel egyező, $D$ pedig a közeg diffúziós együtthatója.
Az ingadozásjelenségekkel az utóbbi évtizedekben, igen sokat foglalkoztak a kutatók. E kutatásoknak elvi és gyakorlati szempontból egyaránt igen érdekes eredményei vannak. Különösen érdekesek és fontosak ezek az eredmények a mérések pontosságának lehető növelése szempontjából. Úgy gondoljuk, nem lesz érdektelen néhány ilyen probléma bemutatása.$^{16}$
A kisérleti fizikának egyik fontos feladata, hogy újabb és újabb mérések lefolytatásával és egyre érzékenyebb műszerek szerkesztésével állandóan növelje a mérési eljárások pontosságát. A század elején valamennyi fizikus abban a hitben volt, hogy a technika fejlődésével valamennyi mérés hibája elhanyagolhatóan kicsinyre csökkenthető. Természetesen azt már akkor is tudták, hogy a mérési folyamattal szükségszerűen együtt jár a mérendő tárgy és a mérőeszköz közötti kölcsönhatás. Ily módon a mérési folyamat szükségszerűen befolyásolja a mérési eredményt. Ez azonban - úgy vélték - csak a mérés pontos lefolytatását nehezíti, de annak pontosságát végső soron nem korlátozhatja. S valóban nem alaptalanul várjuk, hogy a tárgy és a mérőeszköz kölcsönhatásában fennáll valamilyen szabályszerűség, melynek alapján a kölcsönhatásból eredő zavar kiszámítható.
Ugyanakkor már kifejlődőben volt az anyag kinetikus elmélete. A kinetikus elmélet statisztikus jellegéből következik, hogy az ily módon értelmezett fizikai mennyiségek szabálytalan ingadozásoknak vannak alávetve. Nyilvánvaló, hogy az ingadozások befolyásolják e fizikai mennyiségek mérésének pontosságát is. A probléma számszerű megfogalmazásához és az ún. ingadozásjelenségek elméletének kiépítéséhez az első lépést Einstein és Smoluchowsky tették meg (1905). Az említett kutatók abból az elgondolásból indultak ki, hogy a kolloid‑részecskék Brown‑mozgása a molekulák hőmozgásának következménye. Az elméletnek jelentős sikere volt; segítségével sok olyan jelenség létezését meg lehetett jósolni, amelyet addig nem ismertek. Így Einstein előre megállapította, hogy zárt áramkörben fel kell lépnie spontán elektromos áramnak is, az elektromos töltések hőmozgása miatt. Érdekes, hogy ez a jelenség csak jóval később vált megfigyelhetővé s a gyenge áramok elektroncsöves erősítőkkel történő erősítésével nyert komolyabb jelentőséget.
Az említett és más hasonló ingadozásjelenségek megismerése nyilvánvalóvá tette, hogy a statisztikai átlagként értelmezett mennyiségek mérésénél az abszolút pontosság lehetetlen, sőt erre még gondolni is értelmetlenség. Ismeretessé vált tehát egy olyan tényező, amely a mérés pontosságának határt szab. Azonban az új elmélet más vonatkozásban is szükségessé tette a mérések pontosságára vonatkozó régebbi elképzelések módosítását. És ezek az az újabb szempontok már sokkal súlyosabbaknak mutatkoztak.
A molekulák hőmozgása következtében ugyanis nemcsak maguk a statisztikusan értelmezett mennyiségek mutatnak szabálytalan ingadozást, hanem a hőmozgásból származó Brown‑mozgás magára a mérőműszerre is kihat. Nézzük meg ezt a kérdést egy példával kapcsolatban. Gyenge elektromos áramnak tekercses galvanométerrel való mérésekor nemcsak az elektromosság áramlásában lépnek fel szabálytalan ingadozások, de a műszer mozgó részei is végeznek Brown‑mozgást; a mozgó tekercs belsejében levő mágneses tér változása is újabb szabálytalanul változó elektromos feszültséget fog indukálni. E szabálytalanságok mind rátevődnek a mérendő áramra, miáltal a mérési eredmény pontossága elmosódik. Hasonló problémák adódnak gyenge sugárzások mérésénél stb.
A mérési eredmények ingadozásának harmadik és legkellemetlenebb fajtáját azok az esetek jelentik, amikor nem tudjuk, honnan ered a folyamat véletlen jellege. Ide tartozik az ugyancsak régen ismert radioaktív sugárzás esete. Régen tudott kísérleti tény, hogy a radioaktív sugárzás szabálytalanul ingadozik. Azonban a modern kvantumelmélet megszületéséig (1926) még csak nem is sejtették, milyen tényezőkön múlik ez a jelenség.
Térjünk most már a bevezetőben ismertetett bizonytalansági relációkra, és vizsgáljuk meg ezek fényében, hogyan lehet a felhozott példák és más hasonló problémák esetében lehetőleg maximális pontosságú mérést végezni. Első pillanatra úgy látszik, hogy egyetlen mennyiség mérési pontossága bizonytalansági relációktól független, hiszen ezek a relációk mindig bizonyos mennyiségpárok egyidejű mérésére vonatkoznak. Sajnos, ez a látszat csalóka, amit igen egyszerűen beláthatunk.
Végső fokon ugyanis bármiféle mennyiség mérése valamilyen műszer mutatóállásának leolvasásából áll. Tehát a közvetlenül mérendő és mérhető adat a mutató helyzete. A mutató azonban mozog, és mozgás közben a leolvasás nehezebb, vagyis a mozgás zavarja a pontos mérést. A hiba kiküszöbölésére megfelelően befolyásolni, szabályozni kell a mutató sebességét, ezzel azonban menthetetlenül fellép a másik adat, ti. a mutatósebesség számbavételének szükségessége is. Látjuk tehát, hogy mivel végső fokon egyetlen mennyiséget önmagában mérni nem lehet, a bizonytalansági reláció mindenféle mérésnél szerephez jut. Másrészről bármilyen mérést is kell végeznünk, mindig véges időtartamot kell fordítani e művelet elvégzésére. Ez a körülmény ugyancsak felveti az iménti problémát, amennyiben a mérendő mennyiség pontossága és a mérési időtartam közt szintén fennáll egy bizonyos fajta határozatlansági reláció.
A fent mondottakkal kapcsolatban szükségszerűen felmerül a kérdés: milyen ismeretelméleti következményei vannak a megismert törvényszerűségeknek? Első pillanatra úgy látszik, hogy a mérés pontosságának korlátai olyan természetűek, amelyek egyúttal az anyagi világ megismerhetőségének is korlátai. Meg kell tehát vizsgálnunk ezt a kérdést is. A fizika törvényei valóban az agnosztikus álláspontot támogatják, vagy esetleg van valamiféle kiút a nehézségekből? A probléma igen nehéz és komolyabb matematikai apparátus nélkül minden igényt kielégítő és meggyőző választ nem adhatunk. Némi egyszerűsítéssel azonban találhatunk a matematikában járatlan olvasó számára is hozzáférhető magyarázatot.
Mindenekelőtt vegyük figyelembe, hogy a statisztikusan értelmezett mennyiségek mérési pontatlansága magából e mennyiségek lényegéből ered: a pontatlanság már a szóban forgó mennyiségek értelmezésében benne van, így a mérésben is mutatkoznia kell. Van‑e értelme egyáltalán annak, hogy ilyen esetekben pontosabb értelmezést keresünk? Nyilvánvalóan nincs, hiszen a statisztikusan értelmezett tulajdonságok csak statisztikusan léteznek, így megismerésük nem lehet pontosabb, mint az értelmük. Példaként gondoljunk a népsűrűség ugyancsak statisztikus értelmű fogalmára. Egy nagy város népsűrűsége elég jól definiált számérték, hiszen a véletlen ingadozás éppen a lakosok nagy számához viszonyítva elhanyagolhatóan kicsiny. Egy kerületet, majd annak egyre kisebb részét, végül pl. valamely házcsoportot tekintve, a viszonylagos ingadozás egyre nagyobb lesz. Végül, ha egészen kis házcsoport népsűrűségét vizsgáljuk, az ingadozások igen nagyok lesznek. Ad absurdum folytatva: egyetlen embernyi terület népsűrűségéről már nem is beszélhetünk. Tehát a statisztikusan értelmezett mennyiségek jellegükből folyó módon már eleve pontatlanok, ennek megfelelően mérésük sem lehet pontos. Itt tehát nem a megismerhetőség korlátaival találkoztunk.
Nehezebbnek látszik a mérőműszer természetéből származó pontatlanság feloldása. Elvi nehézség azonban itt sincs: megfelelő mérőműszer konstruálásával a bizonytalansági relációban szereplő szórásmennyiségek tetszés szerint kicsivé tehetők oly módon, hogy a viszonylagos hiba szintén kicsi legyen. Igaz, hogy abszolút pontos mérés ily módon nem valósítható meg, de a pontosság mindig javítható. A megismerésnek tehát itt sincs áthághatatlan korlátja: mindig többet tudhatunk, de az abszolút pontos ismeret a végtelen távoli időkbe tolódik. A dolog gyakorlati oldalát tekintve még kedvezőbb a helyzet, hiszen igazán nem érezzük semmi hátrányát annak a körülménynek, hogy a kimért szövet hosszát pl. csak milliméternyi pontossággal tudjuk meghatározni. Ennél nagyobb pontosságnak nincs gyakorlati jelentősége, így nincs is rá szükség. Természetesen olyan esetekben, midőn valamilyen okból nagy pontosságra van szükség, igen fontos a műszert jellemző szórásmennyiség ismerete. Hiszen éppen ezen ismeret birtokában tudjuk azt is megmondani, milyen változtatást kell a műszeren és az egész mérési folyamaton végrehajtani ahhoz, hogy a szórásmennyiség kisebbé váljék, és így pontosabban mérhessünk. Ezért igen nagy jelentősége volna a kinetikus elmélet oly mélységig hatoló kiépítésének, hogy a molekuláris szerkezet ismerete alapján a szórásmennyiséget már előre tisztán elméleti úton meghatározhatnánk. Az ilyen irányú kutatások már igen hasznos részleteredményeket szolgáltattak, de az általános elmélet kialakítása ez ideig még nem sikerült.
IV. CLAUSIUS "HŐHALÁL"‑TÉTELÉNEK KRITIKÁJA
1. A Clausius-féle "hőhalál"‑tétel
A múlt század közepe táján gyakran idézett közmondás volt: "tres medici, duo athei" (három orvos közül kettő istentagadó). A medikus (az orvos) itt a természettudós megszemélyesítője, az ateista jelző pedig tulajdonképpen materialistát jelent. A közmondás csakugyan a való helyzetet tükrözte. Az atomos szerkezetre utaló alapvető törvények, az elektromosság és a mágnesség ugyancsak alapvető törvényeinek, az energia megmaradása elvének stb. felismerése egyre jobban megerősítette az anyag objektív létezésének és megismerhetőségének nézetét: a materialista világnézetet. E felfedezések világszemléleti hatása széles körökben érezhetővé vált, ezt maguk az idealista világnézet képviselői is kénytelenek voltak elismerni.
A világnézetek közötti rendkívül bonyolult harc során az ellentámadás rövidesen bekövetkezett. A hőelmélet egyik tételét a világegyetem egészére vonatkoztatva egyesek a fejlődés megszűnésére következtettek. Ezen elgondolás szerint a termodinamikai folyamatokkal együtt járó entrópianövekedéssel (vagy ami ezzel azonos: az intenzitásmennyiségek folyamatos kiegyenlítődésével) párhuzamosan a hőjelenségek fokozatosan megszűnnek, és egyidejűleg megszűnik a további fejlődés minden lehetősége. A világnak ily módon bekövetkező állapotát nevezték "hőhalál"‑nak.
Az előzőekben már többször említettük, hogy a világegyetem hőhalálának gondolatát Clausius vetette fel. Történeti hűség kedvéért hallgassuk meg magát Clausiust, mit mond erről a kérdésről:
"... amikor e tétellel a világegyetem egy általános alaptörvényszerűségét kívánjuk kifejezni, a következőképpen fogalmazhatjuk: az energia egyik formája átalakulhat, ugyan az energia másik formájává, de eközben az energia mennyiségéből sohasem veszhet el semmi sem, a világban előforduló összes energia éppoly állandó, mint a világban meglevő összes anyagmennyiség.
Bár a tétel helyessége kétségtelen és bizonyos igen fontos vonatkozásban a világegyetem változtathatatlanságát fejezi ki, mégis túlságosan messzire mennénk, ha úgy gondolnánk, hogy e tétel szerint a világegyetem tulajdonképpeni állapota a változatlan és örök körforgás. A mechanikai hőelmélet második főtétele e nézetnek a leghatározottabban ellentmond. (...)
A természeti erőkben, a világmindenség jelenlegi mozgásállapotában felhalmozott munkavégző képesség lassanként mindinkább hővé alakul át. A melegebb testekről hidegebbekre átáramló és ezáltal a meglevő hőmérsékleti különbségek kiegyenlítésére törekvő hő lassanként mindinkább egyenletes eloszlású lesz: az éterben meglevő sugárzó hő, valamint a testekben felhalmozott hő között is bizonyos egyensúly fog beállani. Végre a testek molekula‑elrendeződése is bizonyos állapothoz közeledik, amelyben az uralkodó hőmérséklet mellett a diszgregáció egészben véve a lehető legnagyobb lesz.
Én ezt az egész folyamatot egyszerű tétellel próbálom kifejezni, mely azt az állapotot is, amely felé a világ lassanként halad, határozott módon jellemzi. Megalkottam egy mennyiséget, amely az átalakulások jellemzésében ugyanazt a szerepet játssza, mint az energia a hőre és munkára nézve (...). Ezt a mennyiséget entrópiának neveztem el. Mindazon esetekben, amelyekben a pozitív átalakulások nagyobbak, mint a negatívak, az entrópia növekszik. Arra kell tehát következtetnünk, hogy a természeti jelenségek összességénél az entrópia összértékének mindig növekednie kell és sohasem csökkenhet. Így a mindenütt és állandóan végbemenő átalakulási folyamat rövid kifejezéséül a következő tételt kapjuk: a világ entrópiája maximum felé törekszik.
Minél jobban közeledik a világ az entrópia‑maximum határállapotához, annál inkább csökken a további változásokra hajtó törekvés, és ha ez az állapot végre bekövetkezett, akkor nincs többé változás sem: a világ holt állapotba kerül.
Bár a világ jelenleg messze van ettől a határállapottól, és bár az ehhez való közeledés oly lassan történik, hogy mindazok az időközök, melyekkel a történelmet mérjük, rövid arasznyi szakaszok csupán ahhoz az iszonyúan hosszú időhöz képest, amelyre a világnak még az aránylag kis átalakulásokhoz is szüksége van; mégis fontos eredmény az, hogy olyan természeti törvényt találtunk, amelyből biztosan következtethetünk: a világban nem minden körforgás, a világmindenség bizonyos irányban állandóan tovább és tovább változik és végső soron egy határállapot felé törekszik."$^{17}$
A materialista és az idealista szemlélet között heves vita indult meg a "hőhalál"‑tétel körül, s ez a vita még ma sem zárult le teljesen. A bizonyítható tények kezdettől fogva a materialista világnézet mellett szóltak, azonban bizonyos hipotézisekből, melyek lehetetlenségét nem sikerült teljes egyértelműséggel bizonyítani, a "hőhalál" bekövetkezésére lehetett következtetni. Maga a tétel a fizikában és a csillagászatban sohasem nyert polgárjogot: a "hőhalál" kérdése kimondottan világnézeti jellegű probléma. Szakemberek körében egy időben valóban felmerült ennek a kérdésnek lehetősége, de komoly formában sohasem tekintették egyenrangúnak a többi fizikai tétellel. Már ezelőtt 50 évvel sem akadt egyetlen fizikus sem, aki ne illette volna kritikával a "hőhalál"‑ra vonatkozó népszerűsítő jellegű megállapításokat.
$\ast $
A "hőhalál"‑tétel nem egyéb, mint a második főtételnek a világegyetemre való alkalmazása. Eszerint: zárt rendszeren belül az entrópia mindig szaporodik és a szaporulattal arányban egyre kevesebb marad forgalomban. Ezzel megáll a világ élete: az intenzitásparaméterbeli különbségek mind kiegyenlítődnek. A fenti következtetést első alkalommal csupán a hőmérséklet kiegyenlítődésével kapcsolatban gondolták végig, ezért nevezték ezt az állapotot "hőhalálnak".
Első pillanatra úgy látszik: itt nem lehet ellenvetés. A materialista az első meglepetés pillanatában csupán gyanakodhat, sejtve, hogy itt valami nincs rendben; és tovább kutat. E továbbkutatás azután kideríti, hogy elhamarkodott általánosításról van szó. A jogos általánosításnak jól meghatározható korlátai vannak, amint ezt a továbbiakban látni fogjuk.
Ne legyünk azonban elfogultak és ne hallgassuk el az újabb keletű idealista véleményeket sem. Egész fejtegetésünk nem sokat érne, ha egyetlen lényegesnek látszót is mellőznénk közülük. Az elmúlt évtizedek során az idealista felfogás is módosult. Íme az egyik ilyen módosulat (mely azonban valamennyi jellegzetességét tartalmazza), Eddington előadásában:
"A régebben szokásos elgondolás szerint, a dolgok végeztekor a világ egész anyagkészlete meglehetősen sűrű, egyenletes hőmérsékletű golyóvá fog tömörülni. De a szférikus tér tana és még inkább a világmindenség tágulására vonatkozó újabb eredmények mindezt megváltoztatták. Vannak tisztázatlan kérdések, melyek nem engedik meg végső következtetések levonását; megelégszem tehát a sok lehetőség közül egynek az elmondásával. Széles körökben feltételezik, hogy a protonok és elektronok végső rendeltetése: egymás megsemmisítése és a bennük rejlő energiának sugárzás alakjában való felszabadítása. Ha ez így van, akkor a világmindenségből végeredményben egy mindinkább ritkuló, mindig nagyobb hullámhosszúságú sugárzásból álló golyó lesz. A sugárzás leghosszabb hullámai a rádióközvetítésre is felhasznált Hertz‑féle hullámok. A rádióhullámok alkotta golyó átmérője kb. minden 1500 millió évben meg fog duplázódni és geometriai haladvány szerint fog növekedni tovább, az örökkévalóságig. Így talán leírhatom a világ végét - egyetlen, lenyűgöző rádió‑közvetítés alakjában."$^{18}$
Látjuk, hogy az idealista felfogás módosulása csupán a világ végének mikéntjére vonatkozik, a lényeg 100 év óta nem változott semmit. Így a kérdésnek ezt a vonatkozását nem szükséges tovább részleteznünk. Nézzük most már az érem másik oldalát. Mi volt a materialista fizikusok gyanakvásának alapja és hogyan igazolta ezt a gyanakvást a hőelmélet és a fizika újabb fejlődése?
Mielőtt a felvetett kérdésekre részletesen válaszolnánk, hasznos lesz, ha még néhány lényeges dolgot elmondunk a kiegyenlítődési folyamatokról és az entrópiáról. Az entrópia fogalmát kezdetben különösen az tette a fizikai szemlélet számára nehezen hozzáférhetővé, hogy először csupán matematikai jellegű segédfogalomként jelent meg a hőelméletben. Ily módon a hőelmélet matematikai apparátusában való szerepe teljesen világos volt ugyan, de nem látszott tisztán, hogy a matematikai forma milyen fizikai tartalmat takar. Ez az állapot aránylag hosszú ideig tartott, és csak az utóbbi évtizedek kutatásainak eredményei után mondhatjuk, hogy az entrópia fogalma, jelentése lényegében véglegesen tisztázódott.
Érdekes körülmény, hogy a hőhalál‑kérdés egész problémaköre teljes egyértelműséggel és a legnagyobb tudományos elmélyültséggel letárgyalható anélkül, hogy az entrópia fogalmát felhasználnánk.
Arra az előbbiekben már részletesen ismertetett tényre gondolunk, hogy az entrópia növekedésének, valamint az intenzív mennyiségek kiegyenlítődésének tételei végső fokon azonos jelentésűek.
2. A "hőhalál"‑tétel érvényesülésének feltételei
Az entrópia‑tétel érvényesülésének jól meghatározott feltételei vannak. Ahhoz, hogy a tétel érvényre jusson, mindegyik feltételének fenn kell állnia. Ha a szükséges feltételek közül csak egy is hiányzik, az entrópia-tétel a kérdéses esetben nem alkalmazható. Tekintsük át röviden a tétel érvényességének szükséges feltételeit.
Az entrópia‑tétel csupán akkor érvényesülhet, ha zárt, véges rendszerre vonatkoztatjuk. Tehát a világegyetem egyes, általunk térben és időben áttekinthető részeiben valóban bekövetkezik a "hőhalál", ha ezek a részek el vannak zárva a környezettől. Az illető rendszer idővel valóban kimerül: minden "életmegnyilvánulás" valóban megszűnik benne. Nyilvánvaló, hogy a világegyetem csak akkor juthat a "hőhalál" sorsára, ha zárt és véges. A "véges" jelzőnek itt egyidejűleg többféle jelentése van, először e jelentések értelmét kell megvizsgálnunk.
A "véges" jelző a térbeli kiterjedésre, az időbeli fennállásra, és nem utolsósorban az anyag tulajdonságainak sokféleségére egyaránt vonatkozhat. Az első két vonatkozás világos; a harmadik már kevéssé, ezért a továbbiakban ennek jelentését és tartalmát is részletesen ki kell fejtenünk.
Az anyag szerkezetére és mozgásformáira vonatkozó ismereteink egyre bővülnek. Ha csak az utóbbi 50 év, de még ha csak az utolsó 10 esztendő eredményeit tekintjük, megállapíthatjuk, hogy az anyag szerkezetének és mozgásformáinak sokféleségére vonatkozó ismereteink egyre gazdagodnak. Joggal merül fel a kérdés: hol itt a határ, illetőleg van‑e egyáltalán határ? Ahogyan a különböző világnézetű fizikusok között vita tárgyául szolgálhat az anyagi világ tér- és időbeli kiterjedésének véges vagy végtelen volta, ugyanígy azt is kérdezhetjük: kimeríthető‑e az anyag tulajdonságainak sokfélesége? Ilyen értelemben tehát harmadik fajta "véges"‑ségről is kell beszélnünk. A végtelenség ebben a vonatkozásban is felboríthatja mindazon számítások érvényét, melyek a világegyetemet véges, zárt rendszernek tekintik.
Az így adódó szempont szerepének megértéséhez a hőelmélet tárgyát és módszereit közelebbről is meg kell vizsgálnunk. A hőelmélet ismeretes kétféle tárgyalásmódja szerint megkülönböztetünk "fenomenologikus" és "statisztikus" hőelméletet.
A fenomenologikus tárgyalásmód megelégszik a szemlélet számára közvetlenül adott hőjelenségek kapcsolatainak vizsgálatával, nem kutatja, hogy ezek a jelenségek az anyag szerkezetével és mozgásformáival milyen kapcsolatban állnak. A fenomenologikus tárgyalásmódban az anyag mint a teret, illetőleg egy‑egy térrészt folytonosan kitöltő szubsztancia jelenik meg, melynek kiterjedése, nyomása, entrópiája, hőmérséklete és még számos egyéb tulajdonsága van; a fenomenologikus szemlélet arra azonban nem ad választ, hogy a nyomás, hőmérséklet és a többi tulajdonság milyen viszonyban van az anyag szerkezeti felépítésében adott tulajdonságaival? Nem tartozik ugyan szorosan ide, de félreértések elkerülése végett megemlítjük, hogy a fenomenologikus tárgyalásmód gyakorlati szempontból nemcsak megengedhető, de szükséges is. Bajt csak akkor okoz, ha alapelveit világmagyarázó elveknek tekintjük. Figyelembe kell tehát venni, hogy a fenomenologikus tárgyalásmód fogalmai és törvényei terjedelmükben és érvényükben korlátozottak. Súlyos hibát követnénk el, ha ezt elmulasztanánk.
A statisztikus tárgyalásmód az anyag molekuláris felépítettségének tényéből indul ki. Ekkor a statisztikus tárgyalásmód alkalmazása feltétlenül szükséges, hiszen a nagyszámú molekulából álló rendszerek tömegjelenségei alkotják a közvetlen szemlélet tárgyát. Így pl. nem az a fontos, hogy a környezetünkben levő levegő egyes molekulái milyen sebességgel mozognak, hanem az, hogy mekkora az átlagos sebességük. Az átlagos sebesség konkrét megnyilvánulása a gáz nyomása és hőmérséklete. Ily módon azonban kiderül, hogy a hőelméleti törvények valószínűségi jellegűek. Mit jelent ez? Tudjuk, hogy a melegítendő vizet tűz fölé kell tenni, és azt is tudjuk, hogy a várt eredmény nem marad el: a víz felmelegszik. Ez azonban elvben nem szükségszerű: bár igen‑igen kis valószínűséggel, de fennáll annak a lehetősége is, hogy a víz megfagy és a tűzhely még melegebb lesz... A nagy számok törvénye (mivel már kis mennyiségű anyagban is igen nagyszámú molekula van) gyakorlatban megment az ilyen meglepetésektől. Azonban nagyon hosszú időn át vizsgálva ugyanazt a jelenséget, egyszer be kell következnie a kis valószínűségű esetnek is. A hőelmélet több, gyakorlatilag is fellépő "ingadozás‑jelenség"‑et ismer. Az ingadozás‑jelenségek akkor válnak jelentősekké, ha egyszerre többféle lehetőség kb. egyenlő valószínűséggel következhet be.
A statisztikus hőelmélet megszületése a hőelmélet, illetőleg a fizika ismeretelmélete szempontjából is jelentős esemény volt. Ugyanis általa a fizikában is polgárjogot nyert a "véletlen" fogalma. Ha pedig meggondoljuk, hogy a dialektikus felfogás szerint a szükségszerűség véletleneken keresztül is megjelenhetik, akkor a hőelméleti fogalmak és a tételek statisztikus jellegét sem hagyhatjuk figyelmen kívül: a statisztikus jellegnek a "hőhalál"‑tétel kritikája szempontjából is jelentősége van, amint azt a továbbiakban szintén látni fogjuk.
A hőelmélet statisztikus jellege nemcsak a véletlen szerepének fontosságára irányítja figyelmünket, hanem az anyag építőköveinek individuális szerepére is. Az anyagon észlelt "nagybani" tulajdonságok és törvényszerűségek végeredményben a "kicsinyben" végbemenő elemi folyamatokból származnak. Ahányfélék lehetnek a kicsinybeni elemi folyamatok, annyiféle az előttünk makroszkopikusan végbemenő kiegyenlítődési folyamatok lehetősége is. A relativitás elméletéből tudjuk, hogy az anyagnak tehetetlen tömegével arányos energiája is van. Mivel az anyag nem semmisíthető meg, energiája is örökérvényű. Azonban a munkavégzés, illetőleg az ezzel egyenértékű energiaátadás mindig csak kiegyenlítődési folyamatok által realizálódhat. A "hőhalál"‑tétel pedig éppen azt állítja, hogy hiába van energiakészletünk, ha a világegyetemben mindenfajta intenzitásparaméter szempontjából egyneműség uralkodik: ekkor már nem jöhet létre újabb kiegyenlítődési folyamat és energiaátadás sem, vagyis a világ energiakészlete tétlenségre van kárhoztatva. Nem nehéz azonban észrevennünk, hogy ebben az okfejtésben hallgatólagosan az a feltevés is szerepel, hogy az energiaátadás csak véges számú s általunk már ismert formában mehet végbe. Az elemi részecskék egymásba való átalakulásainak ismerete és ismereteink szédítő iramú gyarapodása azonban természetesen semmiképp sem jogosít fel erre a feltevésre. Nem hinném, hogy jelenleg már az összes fajta kiegyenlítődési folyamatokat ismerjük és azt sem, hogy még néhányat megismerve a sor valóban bezárulna. Egyetlen átfogó természeti törvény sem követeli meg, hogy az anyagot ne tekinthessük ebből a szempontból is végtelennek. Az örök fejlődésben és átalakulásban levő anyag bizonnyal végtelen az intenzitásparaméterek számát illetően is. E megállapítással talán kissé túl előre léptünk, azonban semmiképpen sem jártunk el tudományellenesen.
Mint látjuk, az anyag szerkezetének és mozgásformáinak figyelembevétele új oldalról világítja meg az entrópia‑törvény jellegét a véletlen szerepével kapcsolatban, és új oldalról világítja meg a kiegyenlítődési folyamatok lehetőségeit is. A "hőhalál"‑tétel kritikájában ezeket a szempontokat is fel fogjuk használni
A "kritika" kellékeinek felsorolása ezzel meg is történt. Következő és egyben utolsó feladatunk, hogy még egyszer sorra vegyük az entrópiatétel érvényesülésének előbb említett feltételeit és megvizsgáljuk, fennállnak‑e ezek a feltételek a világegyetemre vonatkozóan.
Könnyebb áttekinthetőség kedvéért összefoglalóan felsoroljuk még egyszer a megvizsgálandó szempontokat:
- A világegyetem térbeli kiterjedésének problémája
- Milyen feltételt szab az energia és mozgásmennyiség megmaradásának elve a világegyetem időbeli kiterjedésének méretére vonatkozóan?
- Az entrópiatétel érvényességi területe a fenomenologikus elmélet keretében
- A véletlen szerepe a hőelméleti folyamatoknál
- Véges‑e vagy végtelen az energia átalakulási lehetőségeinek száma?
Még egyszer hangsúlyozzuk: ha a fenti szempontok vizsgálata csak egyetlen esetben is tagadó válaszra vezet a "hőhalál" bekövetkezésével kapcsolatban, úgy - egyenként szükséges feltételekről lévén szó - maga a "hőhalál"‑tétel is megdőlt. Azonban nem elégszünk meg egyetlen feltétel vizsgálatával, és kimutatjuk, hogy a világegyetem végső halálát következtető tétel egyik feltétel szerint sem helytálló vagy legalábbis nem szükségszerű.
Mit szólnak új érveinkhez a "hőhalál"‑tétel hívei? Újabb ellenérveiket tartalmazó nyilatkozatot nem ismerek, a kiindulásul szolgáló fenti megállapítások alig néhány évtizedesek. De hasonló - bár kevésbé csattanós - érvek már régebben is voltak a "hőhalál"‑tétellel szemben. Mindenesetre nagyon tanulságos az az "ismeretelméleti módszer", melynek gyakorlására ilyen esetekben sor szokott kerülni, s amit éppen egy Eddingtontól származó idézettel tudnánk legjobban megvilágítani: "2000 körül$\boldsymbol{\large ^\circ}$ Lambda professzor, a híres régész, egy antik görög feliratot talál. Arról van benne szó, hogy egy idegen herceg - bizonyos Κανδείκλης$\boldsymbol{\large ^\circ{}^\circ}$ - népével együtt Görögországba jött és letelepítette törzsét. A professzor azonosítani kívánja a herceget, átnéz minden lehetséges forrást, végül az Encyclopaedia Athenica $\mathrm{C}$ és $\mathrm{K}$ betűjénél kezd el keresgélni. Figyelme megakad egy szócikken Canticles-ről, aki Salamon fia volt. Megvan a kívánt személy, világos, hogy Κανδείκλης azonos Canticles-szel, a zsidó herceggel. Lambda elmélete széles körben elterjed. Abban az időben Palesztina$\boldsymbol{\large ^\circ{}^\circ{}^\circ}$ és Görögország, a két tekintélyes hatalom, szövetséget kötött egymással. A görög miniszterelnök ékesszóló beszédben, elérzékenyülve emlékezik meg a két nép rokonságára mutató újonnan felfedezett történelmi kötelékekről. Rövidesen azonban Lambda professzor ismét átnézi a szócikket, és rádöbben, hogy szerencsétlen félreértés áldozata lett. Salamon énekét (»Song of Solomon«),$\boldsymbol{\large ^+}$ Salamon fiának (»Son of Solomon«) olvasta. A professzor beismeri és kiigazítja tévedését, így azt gondolhatnánk, hogy a Canticles-elmélet természetes módon kimúlt. De a görögök és palesztiniaiak továbbra is hisznek a rokonságban, és a görög miniszter továbbra is erről szónokol. Lambda professzor egyszer meg is próbál tiltakozni, mire a miniszter szigorú hangon ráförmed: »Honnan tudja, tanár úr, hogy Salamonnak nem volt Canticles nevű fia? Ön sem mindentudó.« A professzor - Salamon igencsak széles körben létesített házastársi kapcsolataira gondolván - hirtelen nem is tud erre mit mondani."$^{19}$
Nem nehéz felismerni, hogy az idézet teljes egészében ráillik az általunk vizsgált problémára is.
3. A világegyetem térbeli kiterjedésének problémája
Az ősi primitív elképzelések szerint a világegyetem térbeli kiterjedése véges. A távcső felfedezése és fejlődése, illetőleg a távcső segítségével szerzett megfigyelési anyag azonban a másik lehetőség felé irányította a figyelmet. Az általános relativitás elmélete ismét felszínre vetette a világegyetem végességének gondolatát. E gondolatrendszer keretében ugyanis megfogalmazható olyan hipotézis, mely szerint a világ véges, de határtalan. Hogy ez pontosabban mit is jelent, arra vonatkozóan hallgassuk meg ismét Eddingtont, aki ennek a felfogásnak a híve:
"Okunk van feltenni, hogy a tér dimenzióit illetőleg a világ zárt gömb alakú. A tér bármely irányában haladunk is, mégsem érhetünk a végére, de nem is haladhatunk a végtelenségig: óriási, de nem mérhetetlenül nagy távolság megtevése után ismét indulási pontunkhoz jutunk, miután »körülutaztuk a világot«. Az oly térre, melynek megvan ez az újra visszatérő tulajdonsága, azt mondjuk, hogy véges, de határtalan. A gömbfelszín példája a kétdimenziójú véges, de határtalan térnek; a világmindenségben az összefüggések hasonló fajtáját kell feltételeznünk, de eggyel több dimenzióval. (...) Amikor kijelentem, hogy a tér véges, de határtalan volta nem áll a tapasztalással ellentétben, úgy arra gondolok, hogy nem zárja ki az idegvégződéseink külső jelenségek által való izgatásának azt a módját, mely tényleges észlelésünkhöz vezet. Így tehát, ha a véges, de határtalan tér kínálja a titkosírás legkielégítőbb megoldását, úgy nincs okunk e megoldás elől kitérni."$^{20}$
Mindebből látjuk, hogy itt csupán egy lehetséges hipotézisről van szó. A hipotézis realitásának "indoklása" azonban teljes egészében a szubjektív idealista világnézetben gyökeredzik. Hogy a szubjektív idealista felfogás "nem zárja ki", sőt "kínálja" a tér véges voltának lehetőségét, mint a probléma "legkielégítőbb megoldását", ez elől nekünk "nincs okunk (...) kitérni". Ugyanis most nem az a kérdés, hogy milyen megoldást diktál az idealista - vagy akár a materialista - felfogás, de az, hogy a tudomány eredményei melyik nézet mellett hoznak fel döntő érveket.
Ha a világegyetem térbeli kiterjedésének végessége a csillagászat és a fizika tudománya szerint valóban bizonyított tény lenne, úgy fennállana az egyik szükséges feltétel ahhoz, hogy a "hőhalál" bekövetkezzék. A fentebb már többször említett megállapítások szerint azonban ez még önmagában nem lenne döntő bizonyíték a világ "hőhalál"‑ának bekövetkezése mellett, sőt - mint ezt már ugyancsak mondottuk -, ha a szükséges feltételek közül csak egy is hiányzik, lehetne akár véges is a világegyetem, a "hőhalál" mégsem következik be.
Mindezen feltételezett lehetőségekkel szemben a tény az, hogy sem a csillagászat, sem a fizika nem ismer olyan perdöntő bizonyítékokat, melyek a világmindenség véges volta mellett szólnának. De ennél többet is szeretnénk tudni, ti. azt, hogy a világegyetem térbeli kiterjedésének végtelenségére vannak‑e megdönthetetlen csillagászati és fizikai érveink? Ha most is tartani akarjuk magunkat ahhoz a felfogáshoz, hogy ezúttal nem a materialista (vagy esetleg csak egy materialistának képzelt) felfogás felől akarjuk a fizikát magyarázni, hanem fordítva: a fizikai törvényekben a materialista világnézet bizonyítékait keressük, úgy óvatosaknak kell lennünk. Az óvatosság úgy értendő, hogy többet semmiképp ne mondjunk, mint amennyire a fizika és csillagászat jelenlegi állása szerint elmehetünk. Természetesen nincsenek - a dolog természetéből kifolyólag nem is lehetnek - közvetlen és abszolút döntő bizonyítékaink a világ végtelensége mellett sem. A tudomány mai állása szerint jogában áll az idealistának feltételeznie a világegyetem végességét; sokkal valószínűbb azonban, hogy a világegyetem térbeli kiterjedése végtelen. Mivel azonban teljesen egyértelmű választ sem pro, sem kontra nem tudunk adni, más módon kell döntésre jutnunk.
Még Helmholtz, Clausius kortársa hívta fel a figyelmet arra, hogy nem elég csupán az entrópianövekedés törvényét figyelembe venni. Azt is meg kell vizsgálnunk: milyen módon folyik le időben az intenzitásmennyiségek kiegyenlítődése. Az előzőekben már foglalkoztunk ezzel a kérdéssel és mondottuk, hogy a kiegyenlítődés folyamata csak végtelen távoli időben fejeződhet be.
Ha kicsiny a rendszer kiterjedése, és közvetlen környezete már egyensúlyban van, úgy gyakorlatilag véges időn belül beáll az egyensúly. Másként fogalmazva ez azt jelenti, hogy véges idő eltelte után már annyira kicsiny az egyensúlytól való eltérés, amennyi gyakorlati szempontból teljesen elhanyagolható. Igen nagy méretű testekre alkalmazva azonban ezt a tételt, elvi és gyakorlati szempontból egyaránt végtelen hosszú idő alatt lejátszódó folyamattal kell számolnunk. Ez volna a helyzet véges és zárt világegyetem esetében is.
Tegyük fel egy pillanatra, hogy a világegyetem valóban véges, mondhatjuk‑e azonban, hogy zárt? Nyilván nem, mert pl. a térfogata nem állandó (csillagászati megfigyelések szerint a világegyetem tágul), holott a "zártság" fogalmában benne van a térfogat állandósága is. Bármilyen egyszerű modellt alkotunk is a változó térfogatú világegyetemről, felírva rá a hőelméleti folyamatok egyenletét, az egyenleteket megoldva nem kapunk, - még határesetben (végtelen távoli időpontban) sem kapunk egyensúlyi állapotnak megfelelő megoldást. Méginkább ezt az eredményt kapjuk végtelen kiterjedésű világegyetem feltételezése esetén. Tehát akár véges, akár végtelen a világegyetem, véges időn belül nem juthat a "hőhalál" állapotába.
4. A "hőhalál" az energia- és impulzustétel szempontjából
További kérdés, amelyet meg kell vizsgálnunk: a világ időbeli végességének feltételezése (már az eddigiek alapján is legfeljebb feltevésként használhatjuk a "hőhalál"‑tételt) összeegyeztethető‑e az energia és mozgásmennyiség (impulzus) megmaradásának elvével? Ha ugyanis okfejtésünket enélkül megszakítanánk, jóvátehetetlen félreértésben hagynánk az olvasót. Úgy tűnne, a világegyetem hőhalálának kérdése csupán azon múlik, hogy a hőhalál bekövetkezése összeegyeztethető‑e a hőelmélet második főtételével, vagy pontosabban: következik‑e a második főtételből az, hogy a magára hagyott zárt rendszer véges időn belül örökös egyensúlyi állapotba kerül? Márpedig ennek a kérdésnek sem az impulzus-, sem az energiatételhez nincs semmi köze. Az energia-, az impulzus- és az intenzív mennyiségek kiegyenlítődéseinek tételei egymástól logikailag függetlenek, így egyik helyességéből ill. helytelenségéből sem következtethetünk a többi fennállására, ill. érvénytelenségére.
Más helyen kifejtjük, hogy a II. főtétel megállapításai ellentétben állnak egy olyan megállapítással, mely szerint véges időn belül örökös egyensúlynak kellene beállni. Ha azonban e körülményt valami oknál fogva (pl. ismereteink megbízhatatlanságára hivatkozva) mégsem vennénk figyelembe, egyrészről a tényekkel kerülnénk ellentétbe, másrészről még ilyen áron sem lehetne beigazolni a hőhalál bekövetkezését.
A véges élettartamú mozgási állapot ugyanis szükségszerűen feltételezi a mozgás megindulását. E megindulás kétféleképp képzelhető el. Vagy úgy, hogy a II. főtétel által megengedett statisztikus ingadozásból származtatjuk, vagy úgy, hogy egy mozgást teremtő aktust tételezünk fel. A statisztikus ingadozásra való hivatkozás éppen az előbb már bizonytalannak bélyegzett II. főtételt állítaná vissza jogaiba: a teremtő aktus viszont az energia- és impulzustétellel áll ellentétben.
Ezzel kapcsolatban gyakran szoktak Engels okfejtésére hivatkozni:
"Clausius - ha jól értem - azt bizonyítja, hogy a világot teremtették, tehát az anyag teremthető, tehát elpusztítható, tehát az erő, illetve mozgás is teremthető és elpusztítható, tehát az egész tanítás az »erő$^{21}$ megmaradásáról« képtelenség, tehát az ő ebből levont valamennyi következtetése is képtelenség (...) Clausius második tétele stb. bármilyen formában jelenik is meg, szerinte energia vész el, ha nem mennyiségileg, minőségileg. Az entrópia természetes úton nem semmisíthető meg, ezzel szemben teremthető. A világ óráját fel kell húzni, akkor azután jár, míg egyensúlyba nem kerül, amelyből csak csoda indíthatja meg újra. A felhúzásra fordított energia, legalábbis minőségileg, elveszett és csak külső lökés útján állhat elő újra. A külső lökésre tehát kezdetben is szükség volt, a világegyetemben feltalálható mozgás, illetve energia mennyisége tehát nem mindig ugyanaz, az energiát tehát teremteni kellett, tehát teremthető, tehát megsemmisíthető. Ad abszurdum!"$^{22}$
Engels érvelése valóban világos: ha a világ "órája" egyszer majd "lejár", úgy valamikor fel kellett "húzni". A felhúzáshoz szükséges energiával és impulzussal az anyagi világ előzően nyilvánvalóan nem rendelkezhetett, vagyis a teremtő aktus feltétlenül ellentmond az energia és impulzus megmaradása elvének, ezért feltételezése abszurdum. Ebben a vonatkozásban már nem engedhetünk meg semmilyen hipotézist. Az energia- és az impulzustétel olyan általános érvényű, hogy nélkülük egész fizikai világképünk illuzórikussá válna. Ugyanis nincs az a legegyszerűbb tény, amely ne bizonyítaná ezeket a tételeket. Tényekkel pedig nem állíthatunk szembe egyenrangú félként illúziókat.
5. Az entrópiatétel érvényességének korlátai a fenomenologikus elméletben
Említettük előzőleg, hogy az entrópia‑fogalom és az entrópiatétel első ízben az ún. fenomenologikus hőelmélet keretében nyert megfogalmazást. Ha megfigyeltük az entrópia fogalmával kapcsolatban mondottakat, látjuk, hogy az entrópia fogalmának csak addig van értelme, amíg az intenzitásparaméterek fogalma is értelemmel bír. A hőelmélet alapjainak szigorú vizsgálata azonban kiderítette, hogy csak azokban az esetekben beszélhetünk intenzitásparaméterekről, amikor a vizsgált rendszer nincs túl messze az egyensúlyi állapottól.
Ilyen körülmények között nem csodálkozhatunk Ehrenfest‑Afanasjevának azon a megállapításán, hogy nincs minden rendszernek entrópiája. Az entrópia létezéséhez ugyanis az szükséges, hogy a rendszer állapota közel álljon nyugalmi egyensúlyához, és biztosan bekövetkezzék az egyensúlyi állapot. Az egyensúlytól távol álló rendszereknek tehát nincs entrópiájuk. Mivel pedig a világegyetem is ilyen rendszer, a világegyetemnek sincs entrópiája, így az entrópiatétel sem alkalmazható rá.
Szándékosan fogalmaztuk utóbbi állításunkat ilyen élesen, holott ennek érvénye is vitatható. Ti. ha egy rendszernek nincs is entrópiája, egyes részeinek lehet, és e részek összegére a növekedés törvénye továbbra is érvényes. Megítélésünk szerint azonban nem tudományellenes álláspont az sem, ha határozottan leszögezzük: a világegyetemnek nincs entrópiája, így az entrópiatétel sem alkalmazható rá. Most azonban, hogy nemcsak a hőhalál‑tétel cáfolása a célunk, hanem az is, hogy minél több oldalról és minél tisztábban lássuk a véglegesen még le nem zárható problémát, még nem célszerű eleve mereven elzárkózni a vita elől.
6. A hőelmélet statisztikus jellegéből adódó szempontok
A statisztikus hőelmélet új megvilágításba helyezte a hőelmélet fogalmait és tételeit. Eszerint a hőmérséklet, a nyomás s a többi makroszkopikus jellemző értékeit a kiterjedt anyagot alkotó molekulák bizonyos jellemzőinek átlagos értékei adják. A valóságban észlelt adatok természetszerűleg kisebb‑nagyobb ingadozásokat mutatnak az elméletileg számított átlagértékekhez képest. Az egyensúlyi állapottól erősen eltérő esetben viszont az ingadozások olyan nagymértékűvé lehetnek, hogy az átlagértékek jelentése teljesen illuzórikussá válik. Ezek az esetek azok, amelyekkel kapcsolatban megszokott hőelméleti fogalmaink felmondják a szolgálatot (pl. nincs hőmérséklet és nincs entrópia).
Az a körülmény, hogy a hőelmélet tételei csupán valószínűségi jellegűek, feltétlenül szükségessé teszi a kevésbé valószínű, a legvalószínűbb eseményekre vonatkozó hőelméleti törvényektől eltérő törvényű folyamatok figyelembevételét is. A valószínűségszámítás szerint a kis valószínűségű események, vagyis a hőelméleti törvényeket nem követő folyamatok kis gyakorisággal szintén bekövetkeznek. E lehetőség elől kitérni nem lehet. Ilyen módon nemcsak az egyensúly felé, hanem az egyensúlytól elvezető folyamatoknak is realitásuk van, ami viszont ellentmond a "hőhalál" bekövetkezését állító kijelentéseknek.
A statisztikus hőelméletnek egyik fontos alapvető kérdése (többek között) mai napig sincs részleteiben tisztázva. Ti. az, hogy hogyan történik a változó állapotból az egyensúlyi állapotba való átmenet. A gyakorlati számítások mindig extrém esetre szorítkoznak: két test kölcsönhatásának vizsgálatakor föltételezik az egyes testekről, hogy azok a maximális valószínűségű állapotban vannak. Kis idő- és térbeli méretekre vonatkozóan ez helytálló, különben azonban nem. Ezt azért is szükséges hangsúlyoznunk, mert egyáltalán nem lehetetlen, hogy egyes esetekben a maximális valószínűségű állapot a többi lehetséges, de kisebb valószínűségű állapotokhoz képest kisebbségben marad. (Ez úgy értendő, hogy pl. százféle lehetőség közt van egy, amely az esetek 10 százalékában következik be, míg a többi 99 lehetőség külön‑külön 1 százalékot sem, de együttvéve mégis 90 százalékot jelent.)
Matematikai nehézségek és a kellő előismeretek hiánya miatt nem térhettünk ki a második főtétel tárgyalásakor a kvantumelmélet szempontjaira. Teljesen elhallgatni a kérdést mégsem lehet, különösképpen a "hőhalál"‑tétel szempontjából nem. Ma már világos, hogy a kvantumelmélet nem úgy viszonylik a fizika többi ágához (pl. a klasszikus mechanikához), mint az egymástól idegen jelenségekre vonatkozó elméletek. Végső fokon az egyetlen átfogó, minden fizikai jelenséget magyarázni illetékes diszciplína a kvantumelmélet; a fizika többi ágai ennek csupán (különböző speciális területekre vonatkozó) közelítései. Meg kell magyaráznunk, mit jelent pontosabban ez utóbbi kijelentésünk. Az ún. makroszkopikus testek mechanikai, hőtani, stb. viselkedésének nagy része megérthető a molekuláris szerkezet figyelembevétele nélkül is, nagy része azonban nem. Nyilvánvaló tehát, hogy a makroszkopikus testek tulajdonságai a molekuláris törvényekből, e törvények viszont a molekulákat alkotó elektronok, atommagok, azaz legvégső fokon az elemi részek tulajdonságaiból erednek. Teljes pontossággal értelmezni a fizikai entrópia‑fogalmat és megmagyarázni az entrópianövekedés törvényét tehát csak a kvantumelmélet alapján lehet. Itt azonban egy alapvető nehézséggel kerülünk szembe. A kvantumelmélet kétféle, egymástól idegen folyamatot tart nyilván. A magukra hagyott, más anyagi rendszerekkel kölcsönhatásban nem álló rendszerek ún. spontán folyamatot végeznek. E spontán folyamatok szigorúan determinisztikusak, miközben az entrópia is állandó marad. Ha ezt a törvényt alkalmazzuk jelenlegi problémáinkra (a világegyetem más anyagi rendszerekkel nem állhat kölcsönhatásban), úgy szükségszerűen a világegyetem entrópiájának állandóságát nyerjük következményként. A folyamatok másik csoportját a mérési folyamatok alkotják. A mérési folyamat lényege abban áll, hogy a vizsgált rendszer más anyagi rendszerrel van kölcsönhatásban. (Az ilyen kölcsönhatás még nem zárja ki a termodinamikai értelemben vett zártságot.) A kvantumelméletnek jól ismert törvénye szerint a mérési folyamatok valóban entrópianövekedéssel járnak. Éppen ezen az alapon igyekezett Max Born egy nemrégen megjelent munkájában az entrópiatörvényt bizonyítani. Born rámutatott arra, hogy az entrópianövekedés csakis más anyagi rendszerek hatásának következménye lehet. Ma még korántsem tekinthetjük minden vonatkozásban lezártnak a hőelmélet kvantumelméleti megalapozását, de az eddigi eredményeket figyelembevéve, csak tagadni lehet a "hőhalál" állapotának bekövetkezését állító következtetéseket.
7. Az anyagi világ végtelenségének egy újabb lehetősége. Összefoglaló következtetések
A világunkban végbemenő makroszkopikus folyamatok, mint láttuk, egy‑egy fajta intenzitásmennyiségben fennálló inhomogenitás kiegyenlítődésével kapcsolatosak. Az eddigiekben hallgatólagosan mindig az a feltevés szerepelt, hogy a különböző kiegyenlítődési folyamatok száma véges. Pusztán a klasszikus fizikát felhasználó statisztikus értelmezések valóban erre az eredményre vezetnek, de az egzaktabb kvantumelméleti megalapozás már nem. Eszerint megvan a lehetősége végtelen sokféle kiegyenlítődési folyamat létezésének.
Utolsó (és véleményem szerint egyik legdöntőbb) érv a "hőhalál" lehetetlensége mellett az, hogy az anyag tulajdonságainak sokfélesége kimeríthetetlen, végtelen, és ily módon a kölcsönhatások (kiegyenlítődési folyamatok) lehetősége is végtelen. Bár ezt a kérdést különösképpen nem lehet lezártnak tekinteni, az eddigi ismeretek olyan távlatokat mutatnak, melyek szinte elképzelhetetlenné teszik az ellenkező esetet.
Ezzel megvizsgáltuk azokat a főbb alapkérdéseket, amelyek a "hőhalál"‑probléma megértéséhez szükségesek és hozzásegítenek ahhoz, hogy e kérdésben helyesen lássunk. Összefoglalva a tanulságot, a következőket mondhatjuk: egyáltalán nem helytálló az a megállapítás, hogy a világ "életképes" energiakészlete állandóan csökken és szükségképpen elérkezik egyszer az az idő, midőn az anyagi világban minden fejlődés megáll. Azonban, ha egyszer már felvetődött a probléma és felvillant a lehetőség, a kívülálló szemlélő gyanakodni kezd. A szakember által nyújtható magyarázat ennek megfelelően problematikus. Hiszen ha csak egy kicsit is túllő a célon, azaz többet és biztosabban állít, mint amennyire a tudomány jelenlegi állása feljogosítja, esetleg hiábavalóvá válik a meggyőzésre fordított minden igyekezete. Ezért meg kell világítanunk minden oldalról a kérdést: nem mondhatjuk azt sem, hogy a fizika törvényei százszázalékosan bizonyítják a világ örökös fejlődésére vonatkozó tételt; de azt igen, hogy sok mindenben alátámasztják azt, és hogy nincs a fizikának egyetlen olyan tétele sem, amely kifejezetten az ellenkezőjét állítaná. Végigtekintve a fizika fejlődését, attól az időtől kezdve, hogy a világ "hőhalál"‑ának gondolata egyáltalán felvetődött, a cáfolatok egész sorával találkozunk, melyek közül többet itt is megemlítettünk.
Mindezeket figyelembe véve, bár nem tudunk mindent, a "hőhalál" lehetőségét tudományos szempontból képtelenségnek kell minősítenünk.
Jegyzetek
1. Engels, F.: A természet dialektikája [MEM 20. köt., 400. o.]
2. A flogisztonelmélet a hőanyagelmélet primitívebb rokona a XVII-XVIII. században. Ez elmélet szerint minden test bizonyos mennyiségű flogisztonnak nevezett anyagot tartalmaz, amely a test elégése során eltávozik a testből. Az elméletet Lavoisier döntötte meg, kimutatván, hogy az égéstermékek súlya nem kisebb (de a felvett oxigén súlyával éppenséggel nagyobb) az elégetett test eredeti súlyánál, vagyis az égés során nem távozhatott belőle semmiféle anyag.
3. "Adiabatikus" az olyan folyamat, melyet a változásnak alávetett rendszer környezetétől elszigetelve végez olymódon, hogy e rendszer környezetének sem hőt átadni, sem attól hőt felvenni nem tud. A Poisson‑egyenlet azt mondja ki, hogy pl. egy dugattyúval lezárt s a környezettől elszigetelt hengerbe zárt ideális gáz nyomásnak és $\kappa $ hatványra emelt térfogatának szorzata ilyen viszonyok között állandó. A hatványkitevőben levő tényező, amely egy adott gázra nézve ugyancsak állandó, a gázok fajhőjével van kapcsolatban: $\kappa =\displaystyle \frac{C_p}{C-v}$ ahol $C_p$ az állandó nyomáson, $C_v$ az állandó térfogaton mért fajhő.
4. Ostwald nyomán. [Ostwald, W.: Feltalálók, felfedezők, nagy emberek, Bp., Révai, 1912, 52-54. o.]
5. A termodinamika első főtétele kimondja, hogy ha egy vizsgált rendszerrel $dQ$ mennyiségű hőt közlünk, a rendszer belső energiája $dE$ értékkel megnövekszik és ezenkívül külső testeken $dW$ munkát végez; az energiamegmaradás törvénye alapján: $dQ=dE-dW$.
6. A termodinamikában fontos szerepet játszik a természetben végbemenő folyamatok irányának kérdése. A rendszer különböző állapotváltozásai egyenes és fordított irányban játszódhatnak le: pl.: egy gáz kitágul és összehúzódik. Ha a vizsgált rendszerben egy folyamat fordított irányban is végbemehet, úgy, hogy a rendszer visszajut eredeti állapotába, miközben pontosan ugyanazokon a közbeeső állapotokon halad keresztül, reverzibilis folyamatról, ellenkező esetben irreverzibilis folyamatról beszélünk.
7. "Aequivalenswert" — egyenértékszám
8. "Verwandlungswert" — átalakulási érték, átalakulási szám
9. die Verwandlung = átalakulás
10. Clausius, R.: A mechanikai hőelmélet második főtételéről (1867, Braunschweig, Friedrich Vieweg und Sohn.)
11. Hincsin, A.: A statisztikai mechanika analitikus módszerei [Bp., Akadémiai Kiadó, 1951.]
12. $N!=N$ faktoriális, az 1-től $N$-ig terjedő egész számok szorzata, pl. $5!=1\cdot 2\cdot 3\cdot 4\cdot 5=120.$
13. Ugyanis a fenti függvényegyenlet szerint a leendő függvénynek olyannak kell lennie, hogy a szorzat függvényértéke egyenlő legyen a szorzattényezők függvényértékeinek összegével (ezt jelenti az $f(w_1\cdot w_2)=f(w_1)+f(w_2)$). A logaritmus éppen megfelel a követelménynek, ugyanis, amint az köztudomású, a szorzat logaritmusa egyenlő a szorzattényezők logaritmusának összegével: $\log{(a\cdot b)}=\log{a}+\log{b}$.
14. Közbevetőleg megjegyezzük, hogy megfelelő konvergenciafeltételek kirovásával megszámlálhatóan végtelen sok elemből álló hírkészletre is kiterjeszthetjük vizsgálatainkat, sőt pl. a valószínűségi eloszlások Rényi és Balatoni által értelmezett dimenzió fogalmának felhasználásával nagyobb számosságú sokaságokra is. Mi a továbbiakban a formailag legegyszerűbb esettel foglalkozunk csupán, mivel előírt pontosság mellett a probléma mindig véges számú elem figyelembevételére redukálható.
15. Ha a fentieken kívül egyéb megkötéseket nem teszünk, az $F(I)=F[f(p_1,\ p_2,\ ...,\ p_n)]=g(p_1,\ p_2\ ...p_n)$ függvény ugyancsak az információ egyik lehetséges mértékének tekinthető.
16. A következőkben ismertetésre kerülő problémákat nagyrészt R. Fürth és iskolája kutatásai alapján ismertetjük.
17. Clausius, R.: A mechanikai hőelmélet második főtételéről (1867, Braunschweig, Friedrich Vieweg und Sohn.)
18. Eddington, A.: A természettudomány új útjai [Bp., Franklin, é.n., 71. o.]
19. Eddington, A.: A természettudomány új útjai [Bp., Franklin, é.n., 84. o.. Mivel a történet a Fényes Imre által idézett fordításban nem teljesen érthető, a fordítást az angol eredeti alapján (Sir Arthur Eddington: New Pathways of Science, Cambridge, CUP, 1935.) erősen módosított formában közöljük.]
20. Eddington, A.: A természettudomány új útjai [Bp., Franklin, é.n., 51. sk.o.]
21. Értsd: energia. (A szerző megjegyzése.)
22. Engels, F.: A természet dialektikája [MEM 20. köt., 549. o.]
$\large{^\ast }$Jelen formátumban - a jobb láthatóság kedvéért - ezek az eredetileg apróbetűs szövegrészek is normál méretben olvashatók.
$\large{^\ast{}^\ast}$MEM 20. köt., 378-391. o.
$\large{^\ast{}^\ast{}^\ast}$Clausius, R.: Über verschiedene für die Anwendung bequeme Formen der Hauptgleichungen der mechanischen Wärmetheorie. Annalen der Physik und Chemie, 125, 353-400. o. (1865)
$\boldsymbol{\large ^\circ}$Eddington idézett könyve (amely a new york-i Cornell Egyetemen 1934-ben tartott Messenger-előadásait adja közre) 1935-ben jelent meg.
$\boldsymbol{\large ^\circ{}^\circ}$Mai iskolai kiejtés szerint Kandejklész-nek ejtendő, latinos átírásban: Candicles.
$\boldsymbol{\large ^\circ{}^\circ{}^\circ}$1935-ben a mai Izrael Állam még nem létezett.
$\boldsymbol{\large ^+}$Eddington a Salamonnak tulajdonított ószövetségi Énekek énekére (latinul: Canticum canticorum) utal, amire angolul szokás Song of Solomon, Canticle of Canticles vagy csak egyszerűen Canticles (Énekek) címen is hivatkozni.
(Fényes Imre: Entrópia, Bp., Gondolat Kiadó, 1962.)
