1. furcsaság: felmelegítés majd visszahűtés
Vegyünk egy olyan fémrudat, melynek lineáris hőtágulási együtthatója az egyszerűség kedvéért legyen kerek, de a fémekre jellemző szám:
\(\alpha=10^{-5}\ \mathrm{\displaystyle \frac{1}{{}^\circ C}}\)
A fémrúd kezdeti adatai:
\(T_1=0\ \mathrm{{}^\circ C}\)
\(l_1=3\ \mathrm{m}\)
Melegítsük fel \(T_2=100\ \mathrm{{}^\circ C}\) hőmérsékletre! Számítsuk ki a fémrúd új (2‑es) hosszát!
\[l_2=l_1+\Delta l\]
\[l_2=l_1+\alpha\cdot l_1\cdot \Delta T_{1\to 2}\]
\[l_2=l_1+\alpha\cdot l_1\cdot \left(T_2-T_1\right)\]
Minden adatot írjunk be SI egységben, így megtehetjük, hogy mértékegység nélkül írjuk be őket:
\[l_2=3+10^{-5}\cdot 3\cdot 100\]
\[l_2=3+0,003\]
\[l_2=3,003\ \mathrm{m}\]
Ezután hűtsük vissza a kezdeti hőmérsékletre, vagyis legyen \(T_3=0\ \mathrm{{}^\circ C}\)! Ez alapján a hőmérséklet‑változás:
\[\Delta T_{2\to 3}=T_3-T_2=0\ \mathrm{{}^\circ C}-100\ \mathrm{{}^\circ C}=-100\ \mathrm{{}^\circ C}\]
Számítsuk ki a legvégső hosszt! Ebben a lehűtési folyamatban a 2‑es állapot lesz a "kiindulási" állapot, így
\[l_3=l_2+\Delta l\]
\[l_3=l_2+\alpha\cdot l_2\cdot \Delta T_{2\to 3}\]
Minden adatot írjunk be SI egységben, mértékegység nélkül:
\[l_3=3,003+10^{-5}\cdot 3,003\cdot \left(-100\right)\]
\[l_3=3,003-0,003003\]
\[l_3=2,999997\ \mathrm{m}\]
Azt kaptuk, hogy hiába hűtöttük pontosan a legelső hőmérsékletre, a hossza nem "tért vissza", hanem "picit összement". Mielőtt a furcsaság okát megmagyaráznánk, nézzünk egy másik, hasonló esetet!
2. furcsaság: felmelegítés egy illetve két lépésben
Ugyanezt az \(\alpha=10^{-5}\ \mathrm{\displaystyle \frac{1}{{}^\circ C}}\) lineáris hőtágulási együtthatójú, \(l_1=3\ \mathrm{m}\) kezdeti hosszúságú, \(T_1=0\ \mathrm{{}^\circ C}\) kezdeti hőmérsékletű rudat melegítsük fel $100\ \mathrm{{}^\circ C}$‑ra, egyik esetben "egy lépésben", másik esetben viszont két lépésben: először $50\ \mathrm{{}^\circ C}$‑ra, majd onnan tovább $100\ \mathrm{{}^\circ C}$‑ra. Az első esetet az előbb kiszámoltuk, ekkor a hossza
\[l_{\mathrm{végső}}=3,003\ \mathrm{m}\]
lett. A második esetben először $50\ \mathrm{{}^\circ C}$‑ra melegítjük. Ettől a hossza:
\[l_2=l_1+\alpha \cdot l_1\cdot \Delta T\]
\[l_2=3+10^{-5}\cdot 3\cdot 50\]
\[l_2=3+0,0015\]
\[l_2=3,0015\ \mathrm{m}\]
A következő lépében $50\ \mathrm{{}^\circ C}$‑ról $100\ \mathrm{{}^\circ C}$‑ra melegítjük, vagyis a hőmérséklet‑változás most is \(\Delta T=50\ \mathrm{{}^\circ C}\) lesz. Számítsuk ki a végső hoszt:
\[l_3=l_2+\alpha \cdot l_2\cdot \Delta T\]
\[l_3=3,0015+10^{-5}\cdot 3,0015\cdot 50\]
\[l_3=3,0015+0,00150075\]
\[l_3=3,00300075\ \mathrm{m}\]
Vagyis kicsit más eredményt kaptunk, mint amikor "egy lépésben" melegítettük fel $0\ \mathrm{{}^\circ C}$‑ról $100\ \mathrm{{}^\circ C}$-ra. (Persze érdekes kérdés az is, hogy mi értelme a "két lépésben" melegítésnek, hiszen ha "egy lépésben" melegítjük $0\ \mathrm{{}^\circ C}$-ról $100\ \mathrm{{}^\circ C}$‑ra, a folyamat során akkor is "átmegy" az $50\ \mathrm{{}^\circ C}$‑os állapoton...)
A furcsaságok magyarázata
A furcsaság magyarázatához nézzük meg, hogy mit is jelent a "lineáris" a lineáris hőtágulási törvényben. Nemcsak azt, hogy a testnek valamilyen lineáris (hosszmenti) méretéről beszélünk, hanem hogy ennek hőmérséklettől való függése (a hőtágulási grafikon) egy egyenes képét mutatja, azaz a hőtágulási függvény lineáris:
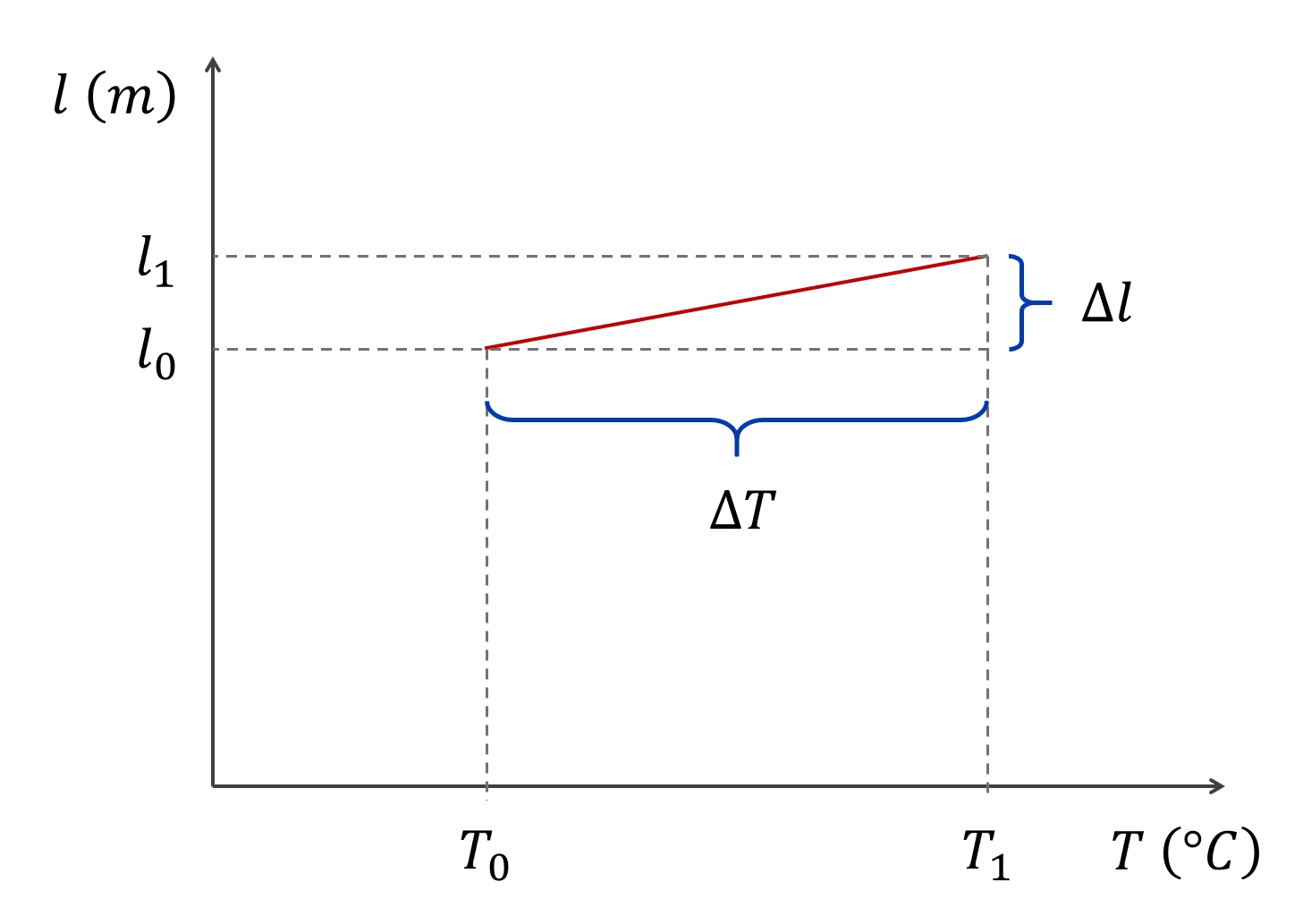
Ha egy függvény egyenes, akkor a meredeksége mindenhol ugyanakkora, tehát állandó érték. A meredekség általánosságban az egységnyi pozitív irányú vízszintes lépés hatására bekövetkező függőleges elmozdulása a függvénynek ("ha egyet lépünk jobbra, mennyit lépünk fel/le")
\[m=\frac{\Delta y}{\Delta x}\]
Most, hőtáguláskor, a függőleges $(y)$ tengelyen az \(l\) hossz van, a vízszintes $(x)$ tengelyen pedig a \(T\) hőmérséklet, emiatt most a meredekség:
\[m=\frac{\Delta l}{\Delta T}\]
A hőtágulási törvény szerint:
\[\Delta l=\alpha\cdot l_0\cdot \Delta T\]
Ezt beírva:
\[m\frac{\alpha\cdot l_0\cdot \Delta T}{\Delta T}\]
\[m=l_0\cdot \alpha \]
Azt kaptuk, hogy a hőméréklet változtatásakor az \(l_0\cdot \alpha \) szorzat mindig állandó. Tehát nem az \(\alpha\) lineáris hőtágulási együttható adódott állandónak. Konkrétabban: ha mondjuk egy \(0\ \mathrm{{}^\circ C}\)‑ról kezdődő, \(100\ \mathrm{{}^\circ C}\)‑ig tartó hőtágulási folyamatot végignézünk az elejétől fogva, illetve "a felétől, \(50\ \mathrm{{}^\circ C}\)‑tól, akkor az utóbbi esetben az \(l_0\) kezdeti hossz már nem ugyanannyi, mint a teljes folyamatban. Emiatt az \(50\ \mathrm{{}^\circ C}\)‑ról induló folyamatnál az \(\alpha\) lineáris hőtágulási együttható már kisebb kell legyen, mint a \(0\ \mathrm{{}^\circ C}\)‑ről kezdődő folyamat esetén. Tehát az \(\alpha\) lineáris hőtágulási együttható hőmérsékletfüggő (például amikor a hőtágulási gradikon egyenes, akkor a hőmérséklettel csökken). Ezért van, hogy ha egy táblázatban megnézzük egy anyag hőtágulási együtthatóját, akkor ott szokott szerepelni zárójelben egy megjegyzés, hogy például ($20\ \mathrm{{}^\circ C}$‑on). Ugyanis különböző hőmérsékletekről indítva a hőtágulást, az $\alpha$ más és más értékű. De az $\alpha$ ilyen módosulása csupán százalékos-ezrelékes nagyságrendű, mivel (szobahőmérsékletről indulva) a legtöbb szilárd anyag pár száz vagy pár ezer Celsius-fokos melegítéstől már megolvad, és az $\alpha$ legfeljebb néhányszor $10^{-5}$.
Vagyis a fenti levezetésekben az volt a hiba, hogy minden kiindulási hőmérsékletnél ugyanazzal az \(\alpha\)‑val számoltunk (a $0\ \mathrm{{}^\circ C}$‑hoz tartozóval), pedig $50\ \mathrm{{}^\circ C}$‑ról vagy $100\ \mathrm{{}^\circ C}$‑ról indulva a hőtágulási együttható ettől eltér.
(Gyakori, de téves elképzelés, hogy a fenti furcsaságok háttere az, hogy a lineáris hőtágulási törvény nem pontos, hanem csak közelítőleg írja le a valódi testek hőtágulását. Ugyan a hőtágulási függvény valóban csak bizonyos hőmérséklettartományban lineáris, akkor is csak közelítőleg, de a fent tárgyalt furcsaságok akkor is fennállnak, amikor a hőtágulási grafikon tökéletes egyenes.)