Az, hogy a Föld forog a saját tengelye körül, ma közismert, azonban a 19. század közepén ezt még csak közvetett megfigyelések támasztották alá:
- csillagászati jelenség: a tengely körüli forgás miatti "napi aberráció" (Bradley, 1728)
- geofizikai jelenség: a Föld egyenlítői kidudorodása
Az "igazi", földi, laboratóriumi kísérleti igazólás sokáig váratott magára. Először Foucault-nak sikerült 1851-ben, híres ingakísérletével. A párizsi Panthéon kupolájából lelógattak egy \(1,4\ \mathrm{mm}\) átmérőjű, \(67\ \mathrm{m}\) hosszú acéldrótot, aminek aljára egy kb. \(17\ \mathrm{cm}\) átmérőjű, \(28\ \mathrm{kg}\) tömegű, sárgarézzel bevont ólomgolyót erősítettek, amitől a drót egyből meg is nyúlt \(5\unicode{x2013}6\ \mathrm{cm}\)-t. Az így kapott gigantikus inga méltóságteljesen, szép lassan, \(T=16,5\ \mathrm{s}\) periódusidővel, \(\approx 3\ \mathrm{m}\) kitérésekkel lengedezett, ahogy az egy hatalmas templomban illendő viselkedés:
Egy lassú, nagy inga önmagában még nem lett volna olyan egetrengető mutatvány, az viszont igen, hogy az inga függőleges lengési síkja a jóslatnak megfelelően igen lassan (nagyjából \(32\ \mathrm{h}\) periódusidővel) körbeforgott, a közönség ámulatára. Ez azt jelenti, hogy a lengési sík óránként már jól megfigyelhető mértékben \(\approx 11,3{}^\circ\)-kal fordult el (a körbefutó "kerítésre" festett skála nagy számai azt mutatják, hogy hány órakor lesz ott a lengési sík). Egy hasonló ingával láthatjuk felgyorsítva mindezt úgy, hogy mindig csak az inga szélső helyzeteiben készítettek képeket:
Annak fizikájáról, hogy az inga miért olyan paraméterekkel rendelkezik, amilyenekkel, nevezetesen:
- az inga hossza igen nagy
- a nehezék (golyó) átmérője jó nagy
- a nehezék (golyó) nagy sűrűségű ólomból van
- a nehezék gömb alakú
ezek okairól itt lehet részletesen olvasni.
Miért nem \(24\ \mathrm{h}\) pediódusidővel fordult körbe az inga lengési síkja, ha a Föld forgásának periódusideje ennyi, a szerkezet pedig pont azt demonstrálta? Azért, mert az inga golyója lényegében vízszintesen mozog, emiatt a
\[\vec {F}_{\mathrm{Cor}}=2m\cdot \left(\vec{v}\times \vec{\omega }\right)\]
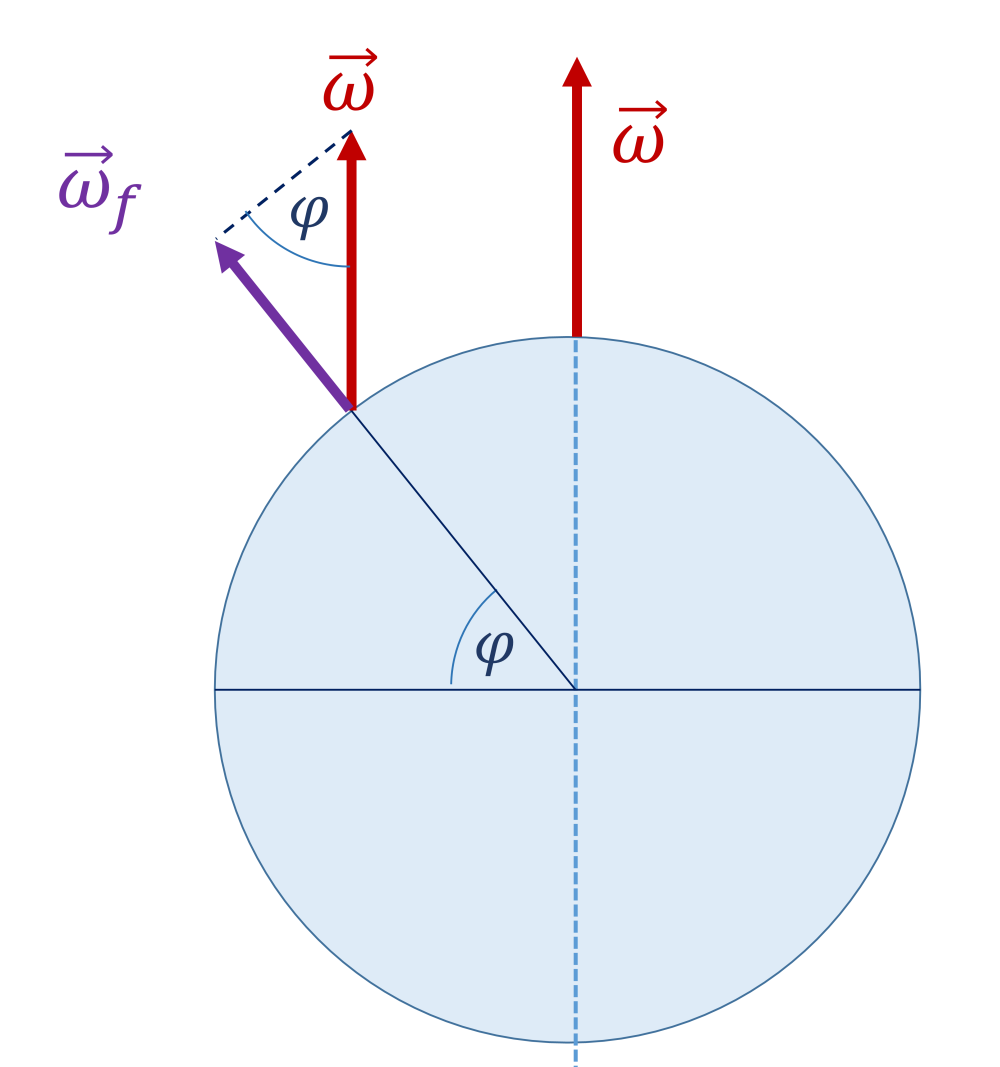
Coriolis-erőben csak a Föld tengely körüli forgását mutató \(\vec{\omega}\) szögsebességnek csak a \(\vec{v}\) vízszintes sebességre merőleges, azaz \(\vec{\omega}_f\) függőleges komponense "forgatja a lengési síkot".
Ez pedig, mivel Párizs a \(\varphi\approx 49{}^\circ\) szélességi körön fekszik, ezért
\[\vec{\omega}_f=\vec{\omega}\cdot \sin{\varphi}=\vec{\omega}\cdot \sin{49{}^\circ}=\vec{\omega}\cdot 0,755\]
ami pedig
\[T=\frac{2\pi}{\omega}\]
alapján nagyobb periódusidőt ereményez, konkrétan:
\[T'=\frac{T}{0,755}=\frac{24\ \mathrm{h}}{0,755} \approx 32\ \mathrm{h}\]
Érdekes, hogy Foucault munkásságából ez az ingás kísérlet messze a legismertebb, pedig tudományos szempontból nem kevésbé jelentős, hogy Fizeau-vel 1849-ben elsőként mérték ki a fénysebességet a Földön (azaz nem csillagászati módszerrer), aminek segítségével 1851-ben meg tudták állapítani, hogy a fény lassabban terjed vízben, mint levegőben. Majd 1862-ben kidolgozta saját fénysebességmérő módszerét (forgótürkös), ami annyira pontos lett, hogy a ma elfogadott értéktől mindössze 0,6%-kal tért el. Műszaki, gyakorlati szempontból nem kevésbé fontos felfedezése, hogy fémekben a változó mágneses mező örvényáramokat kelt (Foucault-áramok). A csillagászok amiatt emlékeznek rá, mert Fizeau-vel először készítettek - a fénykép előfutárának számító - daggerotípiás képet a Napról, amiből arra követleztettek, hogy a Nap felszíne gáz halmazállapotú, továbbá mert egyszerű, de pontos módszert dolgozott ki a tükrös távcsövek csiszolási hibáinak ellenőrzésére.