Áramerősséget mérhetünk digitális vagy analóg műszerrel:
Bármelyikkel is tesszük, a célunk az, hogy minél pontosabban az eredeti áramkörben uralkodó értékeket mutassa a műszer. Csakhogy a műszer bekötése az áramkörbe óhatatlanul megváltoztatja az áramkörben a feszültség- és áramerősségviszonyokat.
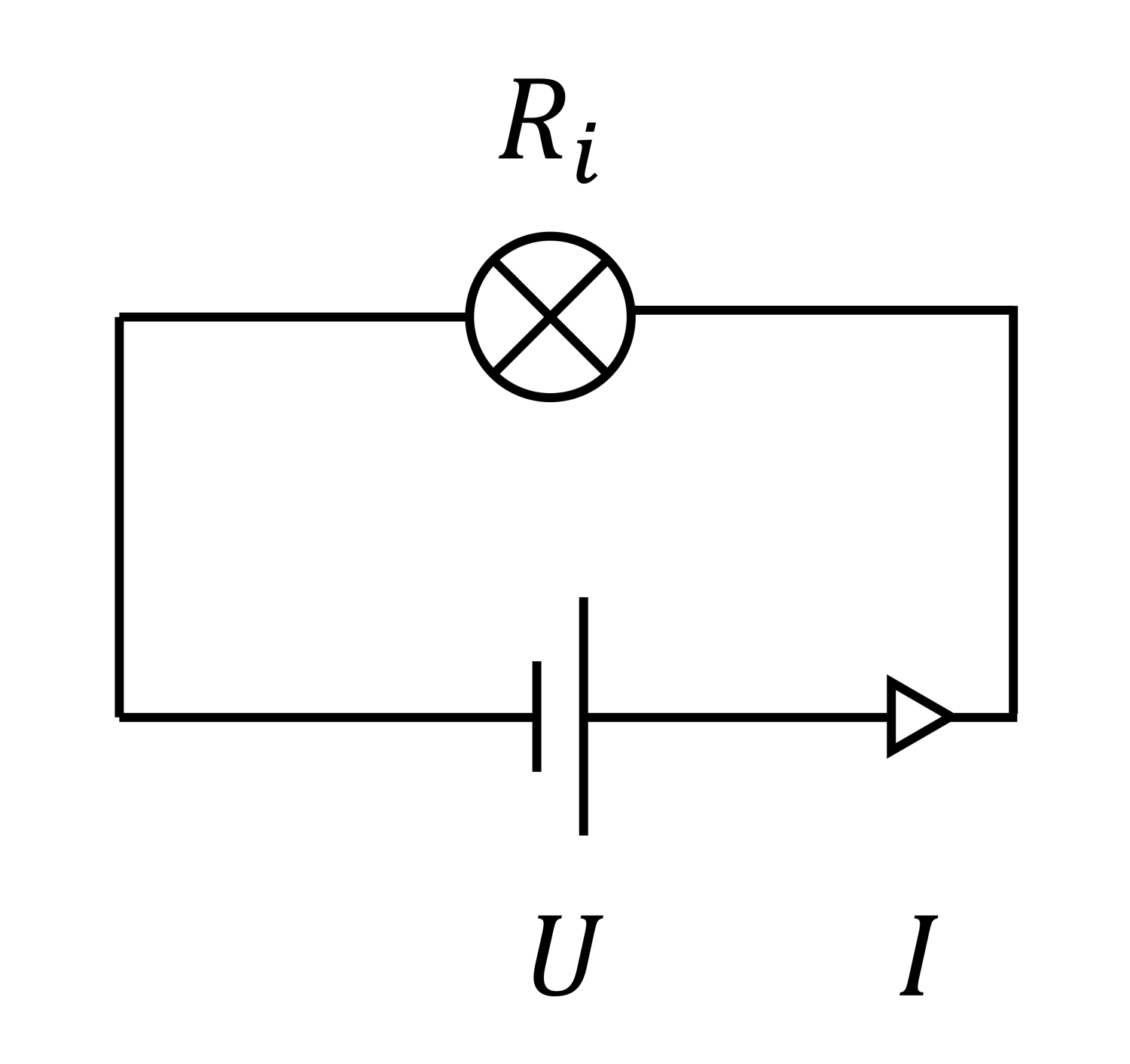
Nézzünk egy egyszerű áramkört, melyben egy állandó \(U\) feszültségű egyenáramú áramforrás táplál egy \(R_i\) ellenállású izzót, amin eközben \(I\) áramerősség halad át:
Mennyi az áramfelvétele az izzónak? Ez Ohm-törvénye alapján kiszámíthatjuk:
\[I={U}{R_i}\]
De nem biztos, hogy ismerjük az izzó ellenállást (mármint a működés közbeni ún. melegellenállását). Ilyenkor a fenti számítással nem tudjuk megkapni az áramfelvételét, ezért azt ki kell mérnünk. Ehhez sorosan kell vele kapcsolni az áramerősségmérőt, hiszen soros kapcsolás esetén lesz azonos a két alkatrészen átfolyó áram:
Csakhogy ezzel megváltozik az áramkör eredő ellenállása, hiszen eddig csak az izzó \(R_i\) ellenállása volt, most meg már van a műszer \(R_m\) ellenállása is:
\[R_e=R_i+R_m\]
ezért az áramforrás \(U\) feszültsége nem ugyanakkora \(I\) áramot fog "átpumpálni", mint eredetileg, hanem egy megváltozott \(I'\) áramot:
Az ideális az lenne, ha az áramerősségmérő beiktatása semennyire nem változtatná meg az izzó áramát, hiszen akkor a műszer az eredeti áramot mutatná. Ehhez az kell, hogy az ampermérő nulla ellenállású legyen, vagyis
az ideális áramerősségmérő-műszer elllenállása nulla (végtelenül kicsi).
Természetesen a valóságban ilyen nincs, de amikor a mérendő áramkörben lévő ellenállásokhoz képest a műszer ellenállása elhanyagolhatóan kicsi (mondjuk ezerszer kisebb), akkor a műszer bekötése csak elhanyagolhatóan kis mértékben változtatja meg a mérendő alkatrészen átfolyó áramerősséget.
A multiméteres leírásában a műszer ellenállása "burden voltage" néven szerepel, méghozzá olyan formában, hogy mekkora feszültség esik a műszeren egységnyi áramerősség hatására; az alábbi kép a Fluke 77IV digitális multiméter adatlapjából való:
A fentiek alapján a műszer ellenállás a \(400 \ \mathrm{mA}\)-es méréshatáron:
\[R_m=\frac{U_m}{I_m}\]
\[R_m=\mathrm{\frac{2\ mV}{1\ mA}}\]
\[R_m=2\ \Omega\]
ami bizonyos szituációkban nem kevés, sőt,akár az is lehetséges, hogy a mérendő alkatrész ellenállásánál is nagyobb. De hát minden műszer csak értő kezekbe való.
(Háklis fizika tanárok idegesek lesznek az "ampermérő" szó hallatán, mert hogy a műszer nem ampert mér, hanem amperben mér áramerősséget. Mindenkinek van valami dilije.)