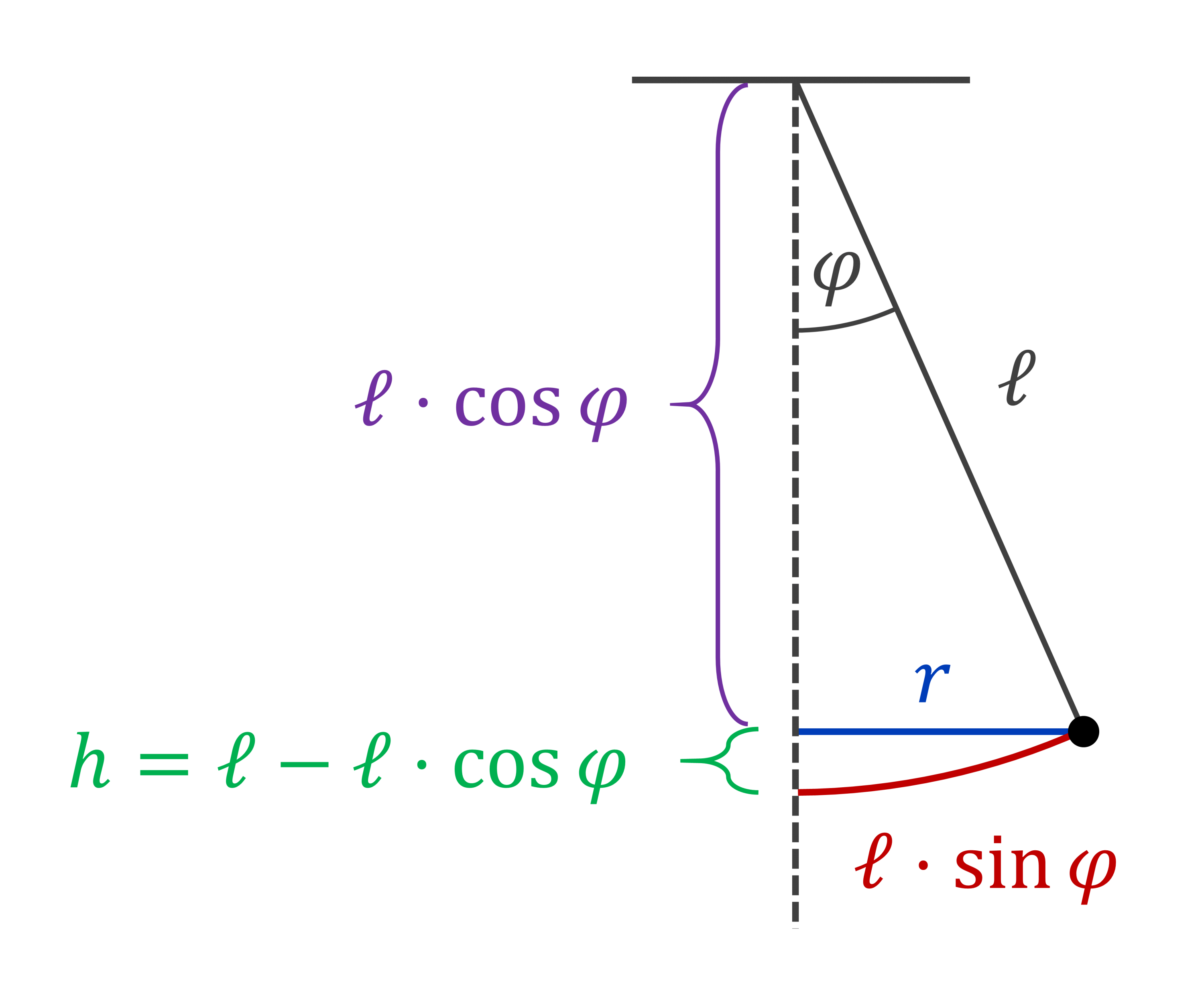Miért szükséges, hogy az inga hosszú legyen?
Ha az Északi- vagy a Déli-sarkon építenénk egy ingát, annak lengési síkja kereken egy nap alatt fordulna körbe (ideális körülmények között; hogy ez mit is jelent, lásd alább). Ha az ingát egyre közelebb költöztetnénk meg az Egyenlítőhöz, attól a körbefordulás periódusideje egyre nagyobb lenne, míg az Egyenlítőn már végtelen naggyá válna, vagyis ott már nem forogna körbe a lengési sík, mert a Föld szögsebességvektorának a függőleges komponense ide érve pont nullára csökken. A legnagyobb sűrűségben lakott mérsékelt égövön az inga lengési síkja nagyjából \(30\ \mathrm{h}\) alatt fordul körbe, vagyis ahhoz, hogy a körbeforduláson komoyabb mérést végezzünk, olyan inga szükséges, ami órákon át tartó lengedezés során sem nagyon csillapodik. Ezzel szemben a hétköznapi tapasztalatainkból tudjuk, hogy egy egyszerű, "házi" készítésű, mondjuk \(1\ \mathrm{m}\) hosszúságú pontinga már pár perc alatt teljesen megáll. Fizika tudás nélkül is érezzük, hogy az órákon át tartó lengéshez valami extrém ingára lesz szükség; talán a nagy ingahossz jelenti a megoldást. De pontosan miért jó, ha hosszú az inga?
A Foucault-ingákról mindig azt mondjuk, hogy van egy lengési síkjuk, pedig ha egy ingát véletlenszerű helyzetben véletlenszerű irányba meglökünk, akkor szinte biztos, hogy az inga még rövid időn át vizsgálva sem egy síkban fog lengeni, hanem "kerülgeti" a középpontot, ráadásul a legszélső helyzetei folyamatosan körbe vándorolnak, de sokkal gyorsabban, mint a Foucault-inga \(\approx 30\ \mathrm{h}\) periódusideje, mondjuk már fél perc alatt:
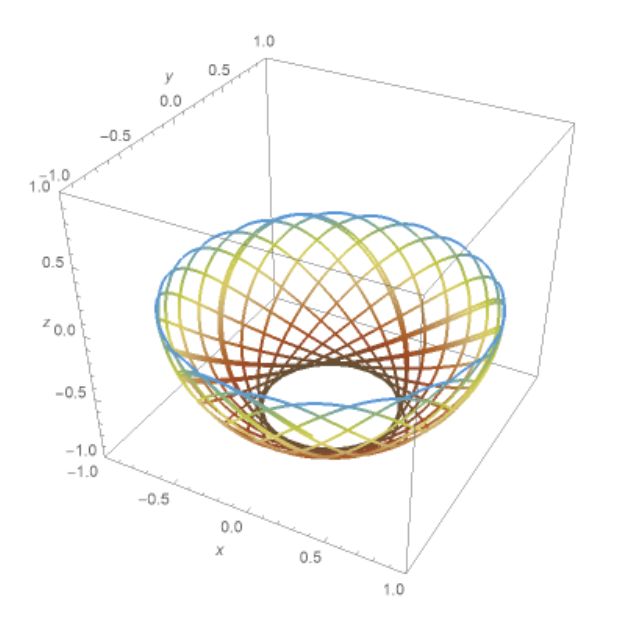
Más szóval a Foucault-inga, mint minden pontinga, igazából gömbi ingának számít. Csak abban a rettentő nehezen előállítható speciális esetben zajlik a lengése egy síkban (rövid időtartamot nézve), ha úgy sikerül elindítanunk, hogy a kezdősebesség pont átmegy az inga nyugalmi helyzete által meghatározott (függőleges) tengelyén. Minden egyéb esetben "rozettaszerűen" körbe-körbe forogva leng az inga. Az alábbi kép ezt szimulálja: a sötétbarna szín a mélyebben lévő állapotokat, a kék pedig a legmagasabban lévő állapotokat jelöli:
Tehát az inga lengési síkja sajnos nemcsak amiatt képes körbeforogni, amit épp ki akarunk vele mutatni (nevezetesen a Föld forgása miatti Coriolis-erő), hanem az inga lengési "síkja" olyankor is folyamatosan körbe forog, ha az ingának a nyugalmi helyzetére (a felfüggesztésen átmenő függőleges egyenesre), mint tengelyre vonatkoztatva van impulzusnyomatéka (perdülete). Tehát ha az indításkor az inga nem precízen a középpont felé indul, hanem "oldalirányban" is van egy kis kezdősebessége. Jelöljük ezt, az ideális kezdősebességre merőleges "káros" sebességet \(\vec{v}_{\bot}\)-sel. Ilyenkor az inga a fenti ábra szerint "precesszálni" fog. Ha ugyanis a golyónak van a középső függőleges tengelyre vonatkoztatva impulzusnyomatéka, akkor annak meg is kell maradnia (tehát a pályaperdület egy mozgásállandó), mivel az inga golyójára ható erőknek erre a tengelyre vonatkozóan sosincs forgatónyomatékuk, ugyanis:
- a nehézségi erőnek azért nincs, mert hatásvonala párhuzamos a tengellyel (mindketten függőlegesek)
- a kötélerő hatásvonala pedig átmegy a tengelyen, emiatt neki sincs forgatónyomatéka
Ez az állandó impulzusnyomaték azt okozza, hogy az inga nem haladhat át a legalsó ponton, hiszen ott a tengelyre vonatkoztatott impulzusnyomatéka eltűnne. Hogy a rozetta mozgás hogyan alakul ki, az már egyetemi tananyag. Számunkra most annyi a fontos, hogy ha az ingával ki akarjuk mutatni a Föld forgását, akkor először is minimalizálnunk kell ezt a "zavaró" effektust, vagyis el kell érnünk, hogy az indításkor az ingának minél kisebb impulzusnyomatéka legyen a függőleges tengelyre.
De egyáltalán miért tenne szert a golyó ilyen \(\vec{v}_{\bot}\) sebességre az elindításkor? Szemléletesen szólva azért, mert a kezünk, amivel a "kimozdított" golyót elengedjük, az egy kicsit remeg. Ez a kézi módszer a legrosszabb módja az inga indításának (inkább egy cérnával kifeszítve, és a cérnát elégetve szokás indítani), de akárhogy is ügyeskedünk, az "elengedő szerkezet" sosem lesz tökéletesen mozdulatlan, mivel a talajban állandóan kisebb-nagyobb rezgásek terjednek, például mert elmegy egy jármű a közelben. Szóval ezt a \(v_{\bot}\) oldalirányú kezdősebességet lehetetlen teljesen kiiktatni, azonban a kísérleti feltételek megfelelő biztosításával erősen lehet csökkenteni, méghozzá olyan kicsire, hogy a minket izgató Coriolis-erő hatása a lengési sk elforgatására már jóval nagyobb legyen, mint a precessziónak a forgató hatása.
A \(\vec{v}_{\bot}\) "oldalirányú" sebesség közelítőleg vízszintes, ahogy a tengelytől a golyóhoz húzható \(\vec{r}\) rádiuszvektor is, ezért az emiatti "káros impulzusnyomaték" vektora függőleges irányú:
\[\vec{N}=\vec{r}\times m\vec{v}_{\bot}\]
Az impulzusnyomaték-vektor hossza:
\[N=m\cdot v_{\bot}\cdot r \cdot \sin{\gamma}\]
ahol a \(\gamma\) szög a \(\vec{v}_{\bot}\) és az \(\vec{r}\) által bezárt szög. Mivel azonban \(\vec{v}_{\bot}\ \bot \ \vec{r}\), azaz \(\gamma=90{}^\circ\), ezért \(\sin{\gamma}=1\), így a káros impulzusnyomaték nagysága:
\[N=m\cdot v_{\bot}\cdot r\]
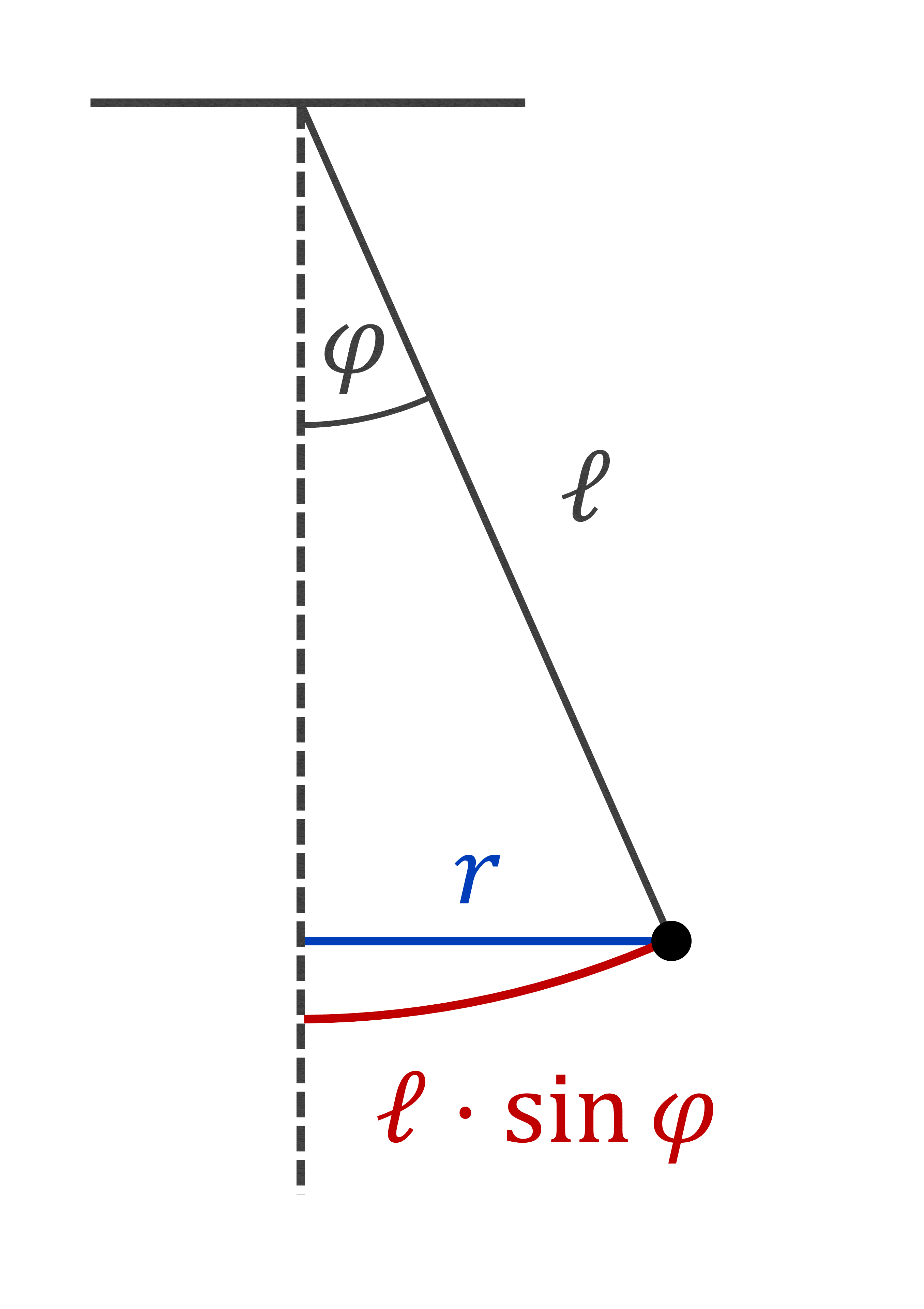
Fejezzül ki \(r\) értékét az inga paramétereivel, vagyis az \(\ell\) hosszával és az inga \(\varphi\) ún. félnyílásszögével (ami az inga drótjának a függőlegessel bezárt szöge)! Kis szögek esetén \(r\) a golyó által bejárt ívhosszal közelíthető:
\[r\approx \ell\cdot \sin{\varphi}\]
Ebből a számunkra káros impulzusnyomaték nagysága:
\[N=m\cdot v_{\bot}\cdot r\]
\[N=m\cdot v_{\bot}\cdot \ell \cdot \sin{\varphi}\]
Hogyan érjük el, hogy ez minél kisebb legyen? A szorzat alapján az alábbi lehetőségeink vannak:
- az \(m\) tömeg csökkentése: ez itt, ebből a szempontból előnyösnek tűnik, de azt azért sejtjük, hogy a minél kisebb tömegű golyó mégsem olyan jó ötlet, hiszen ha a szálló porra gondolunk, ott a pici tömegű porrészecskék lényegében lebegnek a levegőben, vagyis az ő életükben a légellenálási erő a domináns.
- a \(v_{\bot}\) csökkentése: ez minél rezgésmentesebb ingaindítást jelent. Törekedni mindenképpen kell rá, de önmagában ez (akámilyen paramérterekkel rendelkező inga esetén) nem lesz elegendő a mérés sikeréhez.
- az \(r\approx \ell \cdot \sin{\varphi}\) szorzat csökkentése: ez azt jelenti, hogy az inga vízszintes irányú maximális kitérése (nevezzük vízszintes amplitúdónak) legyen minél kisebb. Azonban ezt nem csökkenthetjük nagyon kicsire, más természetű okokból: mi a lengési sík elfordulását akarjuk mérni, márpedig ha mondjuk egy óra alatt \(\theta\) szöget fordul el a lengési sík, akkor az inga köré helyezett henger alakú skálán ez \(\ell \cdot \sin{\varphi}\cdot \theta\) elmozdulást fog okozni. Az alábbi képen a skálán a számok azt mutatják, hogy hány órakor hol lesz a lengési sík. Ezt az elmozdulást annál pontosabban lehet leolvasni, minél nagyobb a vízszintes amplitúdó; mellesleg a lengési sík elfordulása is annál látványosabb. Mivel a lengési sík óránkénti szögelfordulása a helyszín földrajzi szélességétől és a Föld szögsebességétől függ, és hát ezeket a paramétereket nem tudjuk növelni, így muszáj, hogy az elfordulás jól leolvashatósága érdekében \(\ell \cdot \sin{\varphi}\) "kellően nagy legyen".
A párizsi Pantheonban például \(\approx3\ \mathrm{m}\) a vízszintes amplitútó, és mivel a lengési sík óránként \(11,3{}^\circ\)-ot fordul körbe, azaz \(1\ \mathrm{perc}\) alatt 60-szor kevesebbet,
\[\Delta \theta=\frac{11,3{}^\circ}{60}\approx 0,188{}^\circ\]
szöget fordul el, ami radiánban:
\[\Delta \theta=\frac{0,188{}^\circ \cdot 2\pi}{360{}^\circ}\approx 0,00329\]
Ebből a körben elhelyezett skálán való elmozdulás a \(\theta\) szöghöz tartozó ívhosszként adódik:
\[\Delta s=r\cdot \Delta \theta\]
\[\Delta s=3\ \mathrm{m}\cdot 0,0329\]
\[\Delta s\approx 0,01\ \mathrm{m}=1\ \mathrm{cm}\]
Vagyis még 3 méteres (azaz jó nagy) vízszintes amplitúdónál is csak \(1\ \mathrm{cm}\)-t vándorol az inga szélső helyzete percenként a körben elhelyezett skálán. Úgyhogy tényleg nem lehet az \(r\approx \ell\cdot \sin{\varphi}\) vízszintes amplitúdó kicsi.
Összefoglalva: úgy optimalizálhatjuk az inga terveit, hogy először a leolvasási kívánalmak (pontossági elvárás) alapján rögzítjük, hogy legalább mennyi legyen az \(\ell \cdot \sin{\varphi}\) vízszintes amplitúdó, és ezek után megnézzük, hogy milyen egyéb előnnyel vagy hátránnyal járna, ha esetleg az inga hosszát nagyra választanánk. Mindenek előtt nézzük meg, hogy rögzített \(\ell \cdot \sin{\varphi}\) esetén az inga mekkora hossz esetén fog sokáig lengedezni, hiszen órákon át kell "kitartania"!
Az inga összenergiája a légellenállás miatt fog csökkenni: a légellenállási erő negatív munkavégzése fogja "felzabálni", pontosabban szólva disszipálni, szétszórni a környezetbe a kezdeti rendezett mechanikai összenergiát. Nekünk az lenne a jó, ha a légellenállás "lassan emésztené fel" az összenergiát. Vagyis nekünk nem olyan ingahosszt kell választanunk, amikor minél nagyobb lesz az összenergia, hanem, amelyiknél "hosszabb időn át kitart". Hogyan lehetne ezt a gondolatot konkrétan megragadni? Az \(E\) összes mechanikai energia időbeli csökkenését szeretnénk minimalizálni, vagyis ehhez az a jó, ha vagy az \(E\) energia nagy, vagy az időbeli csökkenést megragadó \(P\), mint a disszipatív légellenállási erő teljesítménye kicsi (ideális esetben persze akár mindkettő teljesül, de ne álmodjunk ekkorát). Tehát nekünk az
\[\frac{E}{P}\]
mennyiség a fontos, mert ez azt mutatja meg, hogy hányszor több energiája van az ingának kezdetben, mint amennyit másodpercenként elveszít. Tehát hogy hány másodpercig "tartana ki" a kezdeti összenergia, ha a disszipációs veszteség mindvégig a kezdeti ütemben "fogyasztaná". Bár a disszipáció tempója nem lesz állandó, hiszen a csillapodó, egyre lassabban mozgó golyóra egyre kisebbb légellenállási erő hat, de ez a bonyodalom a gondolatmenetünket nem érinti, mivel akár mekkora is az ingahossz, a disszipáció üteme mindig folyamatosan csökken. Tehát most ki kell fejeznünk, hogy (rögzített \(r\) esetén) hogyan függ az ingahossztól az \(E\) összes mechanikai energia valamint a \(P\), a légellenállási erő teljesítménye. Aztán megnézzük a kettő hányadosát.
Kezdjük tehát az \(E(\ell)\) függés feltérképezésével! Ha a helyzeti energia nullszintjét az inga legalsó helyéhez rögzítjük, akkor kezdetben (kitérítve nyugalmi helyzetben elengedéskor) a golyónak csak helyzeti energiája van, amit az alsó ponthoz képesti \(h\) magassága határoz meg:
vagyis a kezdeti helyzeti energia, ami egynben a golyó összes mechanikai energiája is:
\[E=mgh\]
\[E=mg\ell(1-\cos{\varphi})\]
Ha az inga \(\varphi\) félnyílásszöge kicsi, akkor a koszinuszfüggvényt Taylor-sorba fejtve az első két tag utániakat elhanyagolhatjuk, mivel az elsőkhöz képest nagyon kicsik:
\[\cos{\varphi}=1-\frac{1}{2}{\varphi}^2+\frac{1}{24}{\varphi}^4-\frac{1}{720}{\varphi}^6+...\]
ez alapján
\[-\cos{\varphi}\approx-1+\frac{1}{2}{\varphi}^2\]
amivel az összenergia:
\[E=mg\ell\left(\frac{\varphi^2}{2}\right)\]
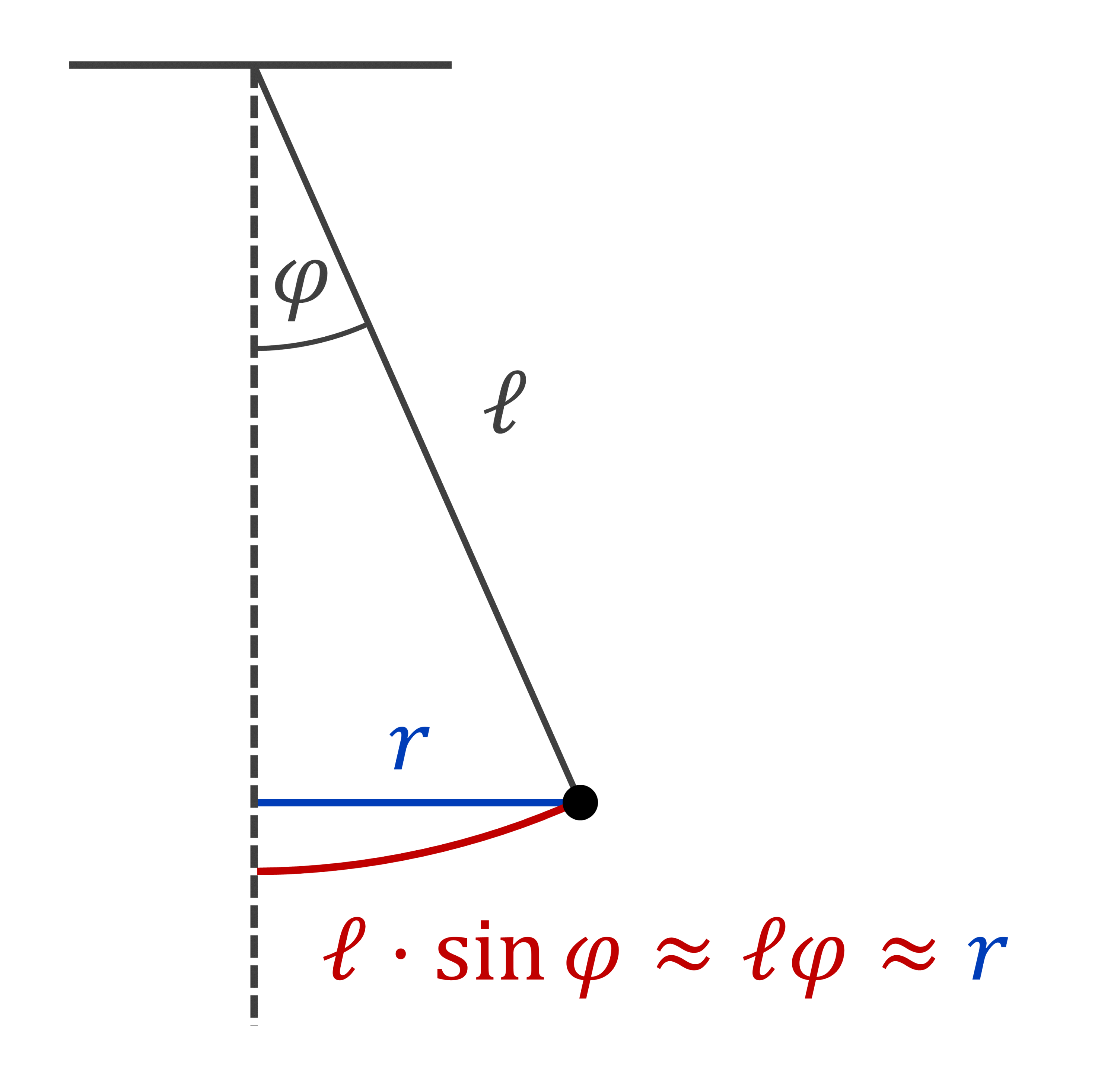
Az általunk rögzített \(r\approx \ell \cdot \sin{\varphi}\) vízszintes amplitúdó kis \(\varphi\) szögek esetén közelíthető a szinuszfüggvény sorfejtése segítségével:
\[\sin{\varphi}=\varphi-\frac{\ {\varphi}^3}{6}+\frac{\ {\varphi}^5}{120}-\frac{\ {\varphi}^7}{5040}...\]
tehát kicsi \(\varphi\) szögek esetén az első taghoz képest a többi tag már mind sokkal kisebb, így azok mind elhanyagolhatók. Ezért kis szögekre:
\[\sin{\varphi}\approx \varphi\]
ami miatt:
\[r\approx \ell \cdot \sin{\varphi}\approx \ell \cdot \varphi\]
így a helyzeti energia:
\[E\approx \frac{mg \ell \varphi}{2}\cdot \varphi\]
\[E\approx \frac{mgr}{2}\cdot \varphi\]
ahol most nekünk \(m\), \(g\), \(r\) konstansok, tehát az összenergia :
\[E\sim \varphi\]
Nekünk most az \(r\) vízszintes amplitúdó fixálva van (kostans),. Mivel a \(\varphi\) félnyílásszög és \(r\) között fennáll:
\[r\approx \ell \varphi\]
\[\varphi \approx \frac{r}{\ell}\]
Ezt beírva az energia iménti kifejezésébe
\[E=\frac{mgr}{2}\cdot \varphi\]
\[E=\frac{mgr^2}{2\ell}\]
ami a konstans tagok alapján azt jelenti, hogy az energia az \(\ell\) ingahosszal fordítottan arányos:
\[E\sim \frac{1}{\ell}={\ell}^{-1}\]
Most következhet a \(P(\ell)\) függés kiderítése! Egy erő teljesítménye mindig az erőnek és az erő irányú sebességkomponensnek a szorzata:
\[P=F\cdot v_{\parallel}\]
Mivel a légellenállási erő golyó alakú test esetén mindig a sebességgel pont ellentétes irányú (nincs "oldalirányú" része), ezért nekünk most a sebességvektor egésze erőirányú, vagyis a párhuzamos alsó index el is hagyható:
\[P=F\cdot v\]
A légellenállás nagyon kicsi sebességek esetén a sebességgel arányos, de a lengedező inga golyója már elég gyors ahhoz, hogy itt a sebesség négyzetével arányos erővel kell számolnunk:
\[F\sim v^2\]
Így a disszipációs teljesítmény:
\[P\sim v^3\]
De hogyan függ a golyó \(v\) sebessége az \(\ell\) ingahossztól (rögzített \(r\) vízszintes amplitúdó esetén)? Mivel az összenergia a legalsó ponban teljesen \(\displaystyle \frac{1}{2}mv^2\) mozgási energiává alakul, és az energiáról már tudjuk, hogy forrdítottan arányos az ingahosszal:
\[\frac{1}{2}mv^2=E\sim \frac{1}{\ell}\]
ebből gyököt vonva azt kapluk, hogy a golyó sebessége arányos az ingahossz gyökének reciprokával:
\[v\sim \frac{1}{\sqrt{\ell}}\]
Ezt beírva a disszipációs teljesítmény hosszfüggésébe:
\[P\sim v^3\]
\[P\sim \left(\frac{1}{\sqrt{\ell}}\right)^3\]
\[P\sim {\ell}^{-3/2}\]
Most már csak egyesítenünk kell az eddigieket:
\[\frac{E}{P}\sim \frac{{\ell}^{-1}}{{\ell}^{-3/2}}\]
\[\frac{E}{P}\sim \frac{{\ell}^{-1}}{{\ell}^{-1,5}}\]
\[\frac{E}{P}\sim {\ell}^{0,5}\]
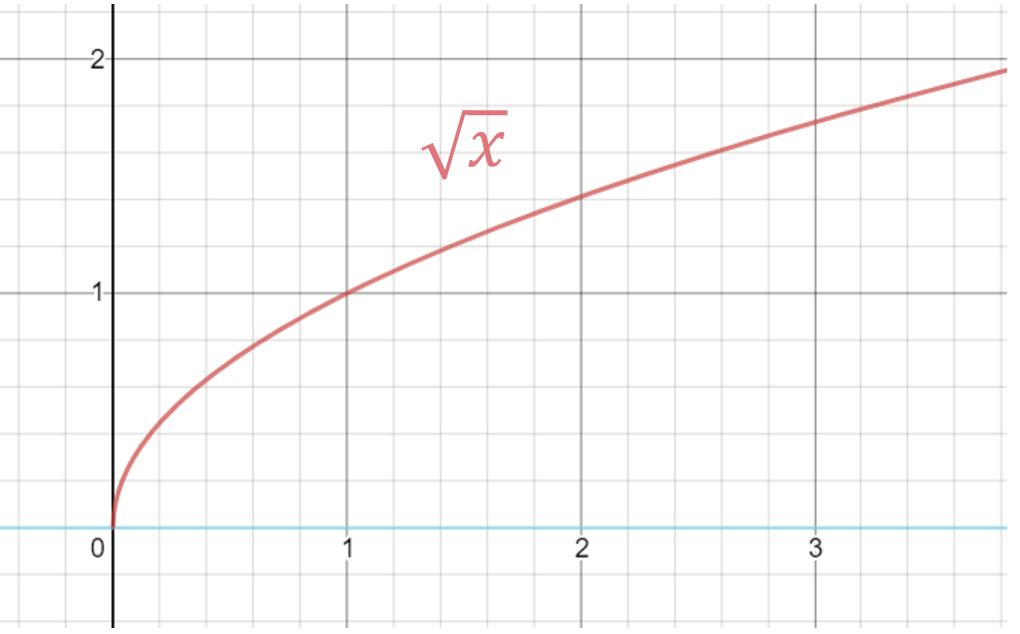
\[\frac{E}{P}\sim \sqrt{\ell}\]
Márpedig a gyökfüggvény monoton növekszik:
Vagyis azt kapuk, hogy rögzített vízszintes amplitúdó esetén annál lassabb ütemben veszíti az inga a mechanikai energiáját, minél nagyobb az ingahossz. Tehát tényleg a nagy hossza miatt tud az óriási inga sokáig lengedezni.
Miért szükséges, hogy az inga golyója nagy méretű legyen?
Nézzük meg, hogy függ az iménti \(\displaystyle \frac{E}{P}\) a golyó \(r\) sugarától (tehát most tekintsük kostansnak a golyó \(\varrho\) sűrűségét)! Azt várjuk, hogy a nagyobb sugár esetén nagyobb lesz. Először nézzük, hogy függ a golyó kezdeti helyzeti energiája a sugarától:
\[E=mgh\]
A tömeg kifejezhető a sűrűség definíciójából:
\[\varrho=\frac{m}{V}\]
\[m=\varrho \cdot V\]
ahol a golyó térfogata a gömbként:
\[V=\frac{4}{3}r^3\pi\]
Ezeket beírva:
\[E=\varrho\cdot \frac{4}{3}r^3\pi \cdot g\cdot h\]
vagyis a szmunkra fonros arányosságot nézve:
\[E\sim r^3\]
Nézzük most adott \(v\) sebességű haladás esetén a légellenálási erő teljesítményét:
\[P=F\cdot v\]
A légellenállási erő a közegként szolgáló levegő \(\varrho_L\) sűrűségétől, a test \(k\) alaki tényezőjétől, a testnek a sebesséégre merőleges \(A\) kersztmetszetétől és a sebesség négyzetétől függ:
\[F=\frac{1}{2}k\varrho_{\mathrm{L}} A_{\bot}v^2\]
ahol a gömb \(A_{\bot}\) merőleges keresztmetszete a kör területe:
\[A=\pi r^2\]
Ezt beírva:
\[P=\frac{1}{2}k\varrho_{\mathrm{L}} \pi r^2v^2\cdot v\]
\[P=\frac{1}{2}k\varrho_{\mathrm{L}} \pi r^2v^3\]
Mivel most minket a sugártól való függés érdekel, a többit konstansnak tekintve az arányosság:
\[P\sim r^2\]
Az eredményeket beírva:
\[\frac{E}{P}\sim \frac{r^3}{r^2}\]
\[\frac{E}{P}\sim r\]
Vagyis tényleg jobb a nagyobb sugarú gömb. (Ezt szokás úgy megfogalmazni, hogy a tömeg a sugár függvényében "gyorsabban", a harmadik kitevővel nő, mint ahogyan a légellenállás, ami "csak" a sugár második kitevőjével.)
Miért ólomból van az inga golyója?
Most tekintsük adottnak a golyó \(r\) sugarát! Ha például vasból és ólomból készítünk ugyanakkora sugarú tömör golyókat, akkor a kezdeti
\[E=\varrho\cdot \frac{4}{3}r^3\pi \cdot g\cdot h\]
helyzeti energia az ólomgolyó esetében nagyobb lesz, mert az ólom sűrűsége \(\displaystyle \left(\varrho_{\mathrm{Pb}}=11\ 340\ \mathrm{\frac{kg}{\ m^3}}\right)\) nagyobb, mint a vasé \(\displaystyle \left(\varrho_{\mathrm{Fe}}=7874\ \mathrm{\frac{kg}{\ m^3}}\right)\). A légellenállási erő valamint annak teljesítménye viszont azonos lesz a két golyó esetén, hiszen a sugaruk azonos:
\[P=\frac{1}{2}k\varrho_{\mathrm{L}} \pi r^2v^3\]
Az ólom ugyan nem a legnagyobb sűrűségű, ismer anyag, hiszen számos fém nehezebb nála, de azok vagy rettentően drágák (arany, platina, ozmium, iridium), vagy a mechanikai tulajdonsága nem jó (a higany sűrűsége \(\displaystyle \left(\varrho_{\mathrm{Hg}}=13\ 534\ \mathrm{\frac{kg}{\ m^3}}\right)\), de szobahőmérsékleten folyékony, így a gömb alakhoz erős tartályt kellene neki készíteni, ami bonyodalom).
Miért gömb alakú az inga nehezéke?
A gömbalak szimmetrikus, minden irányban egyforma, ezért a közegellenállási erő mindig pontosan a sebességgel ellentétes lesz. Ez amiatt fontos, mert ha a légellenálási erőnek lenne a sebességre merőleges ("oldalirányú ") komponense, annak lenne forgatónyomatéka a középső, függőleges tengelyre vonatkoztatva, így az impulzusnyomatékot adna a mozgó nehezéknek, márpedig ez az, amit el kell kerülnünk, hiszen az impulzusnyomatéktól eleve rozettaszerűen forogni fog a lengési sík, mi viszont most nem ezt az effektust, hanem a Coriolis-erőt tanulmányozzuk.