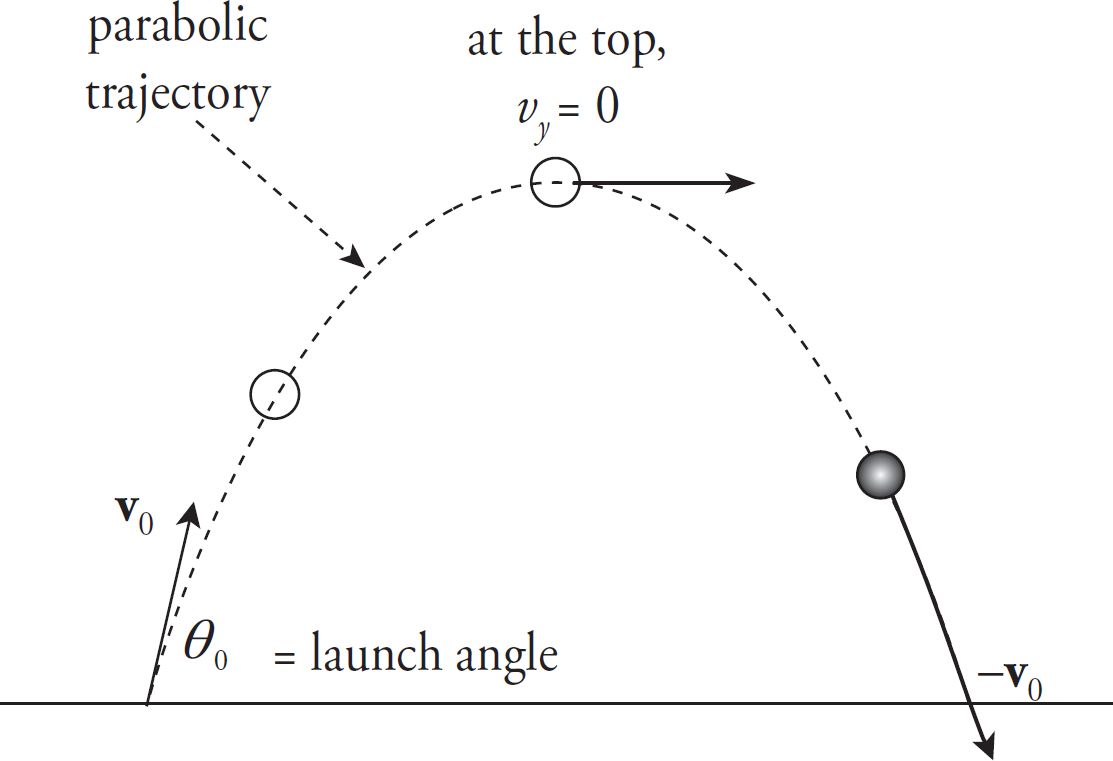
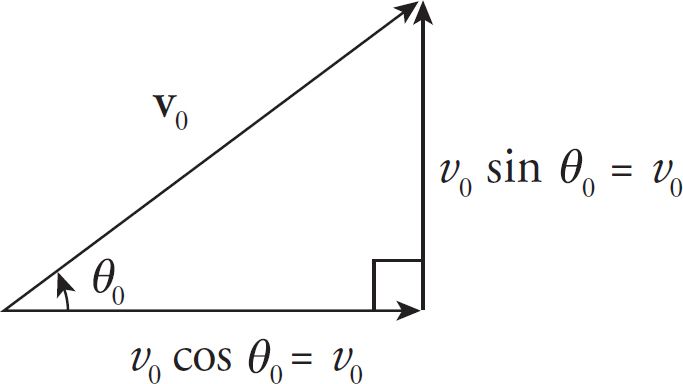In general, an object that moves near the surface of the Earth will not follow a straight‑line path (for example, a baseball hit by a bat, a golf ball struck by a club, or a tennis ball hit from the baseline). If we launch an object at an angle other than straight upward and consider only the effect of acceleration due to gravity, then the object will travel along a parabolic trajectory.
To simplify the analysis of parabolic motion, we analyze the horizontal and vertical motions separately, using the Big Five. This is the key to doing projectile motion problems.
| Horizontal motion: | Vertical motion: |
| $\Delta x=v_{0x}t$ | $y=y_0+v_{0y}t-\displaystyle \frac{1}{2}gt^2$ |
| $v_x=v_{0x}$ (constant!) | $v_y=v_{0y}-gt$ |
| $a_x=0$ | $a_y=-g=-10\ \mathrm{\displaystyle \frac{m}{\ s^2}}$ |
The quantity $v_{0x}$, which is the horizontal (or $x$) component of the initial velocity, is equal to $v_0 \cos{\theta_0}$, where $\theta_0$ is the $\textbf{launch angle}$, the angle that the initial velocity vector, $\textbf v_0$, makes with the horizontal. Similarly, the quantity $v_{0y}$, the vertical (or y) component of the initial velocity, is equal to $v_0 \sin{\theta_0}$.