A potenciális energia
A potenciális energia és helyzeti energia fogalmát a gravitációs mezőnél már bevezettük.
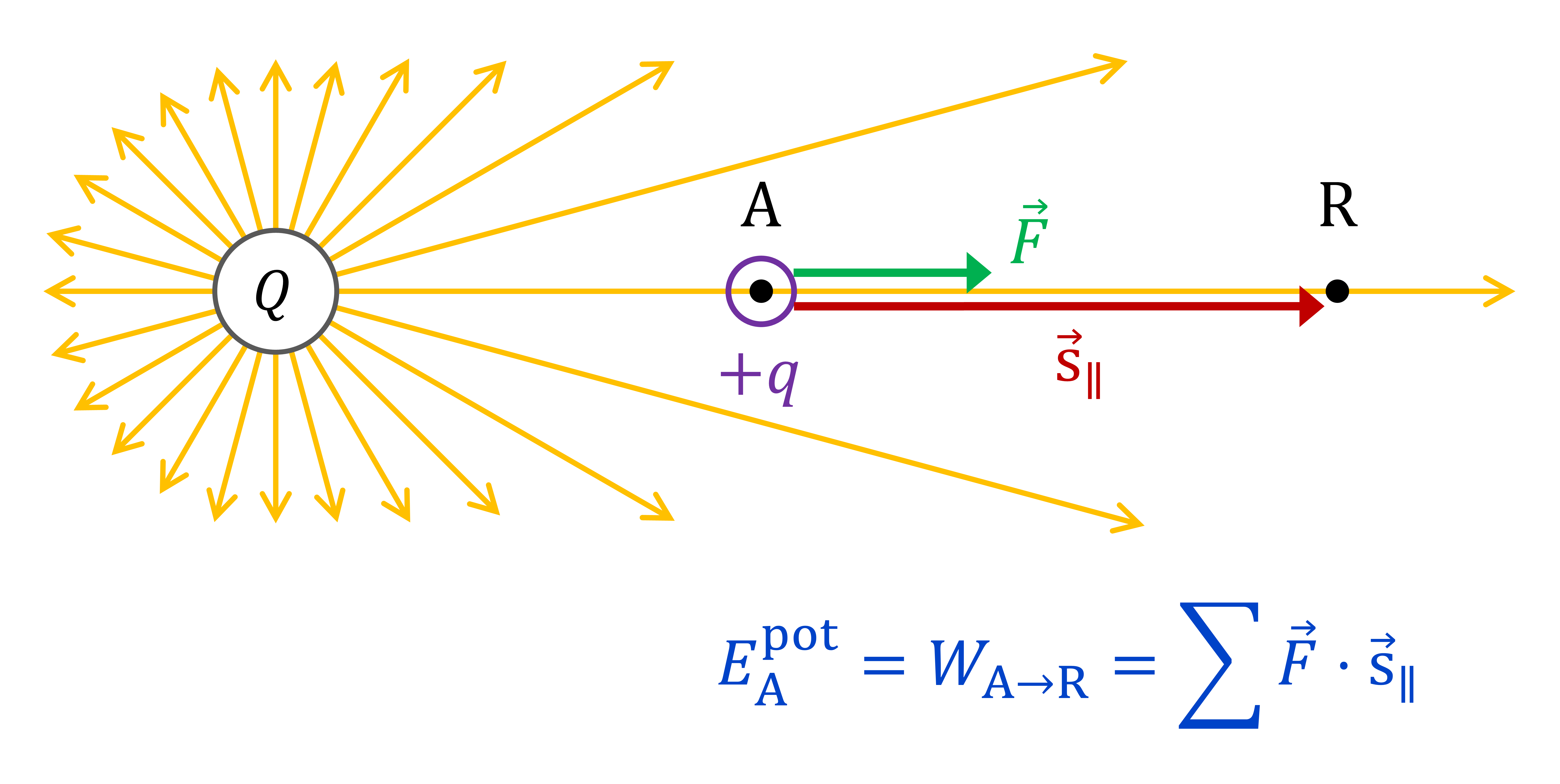
Amikor egy töltés potenciális energiáját akarjuk meghatározni az \(\mathrm{A}\) pontban, vagyis \(E^{\mathrm{pot}}_{\mathrm{A}}\)-t, akkor ugyanazt az eljárást követjük, amit a helyzeti energia esetében tettünk:
- választunk egy helyet, ahol a töltés potenciális energiája nulla és azt elnevezzük \(\mathrm{R}\) referenciapontnak
- megvizsgálunk egy folyamatot, melyben a töltés elmozdul az \(\mathrm{A}\) pontból az \(\mathrm{R}\) referenciapontba
- az elektromos mező munkája az \(s_{\mathrm{A}\to \mathrm{R}}\) mozgatás során megadja az \(E^{\mathrm{pot}}_{\mathrm{A}}\)potenciális energiát
Egy \(q\) töltés \(\mathrm{A}\) pontbeli elektromos potenciális energiáját \(E^{\mathrm{pot}}_{\mathrm{A}}\)-val jelöljük, és az elektromos erő munkáját értjük alatta, miközben a töltés elmozdul az \(\mathrm{A}\) pontból egy átalunk önkényesen választott \(\mathrm{R}\) referenciapontba, amelyben definíció szerint minden töltés potenciális energiája nulla:
$$E^{\mathrm{pot}}_{\mathrm{A}}=\frac{W_{\mathrm{A\to R}}}{q}$$
Ha az \(\mathrm{A}\) pontban lévő \(g\) töltés előjlét meg változtatjuk, ettől a potenciális energiája is ellentétes előjelűre változik, hiszen őt mozgatva a referenciapontba, a rá ható erő mindenhol ellentétes irányú lesz az eddigihez képest, így az erő munkája előjelet vált:
Hogyan változik a potenciális energia különféle irányú elmozdulások esetén?
Vajon ha egy pozitív töltés elmozdul elektromos mezőben különféle irányokba, akkor hogyan változik a potenciális energiája? Nézzünk egyszerű, speciális eseteket:
- a térerősség irányában
- a térerősséggel ellentétes irányban
- a térerősségre merőlegesen
Pozitív töltésre mindig \(\vec{E}\) térerősség irányú erő hat, hiszen a térerősség definíciója: az egységnyi töltésre ható erő:
\[\vec{E}=\frac{\vec{F}}{q}\]
amiből
\[\vec{F}=\vec{E}\cdot q\]
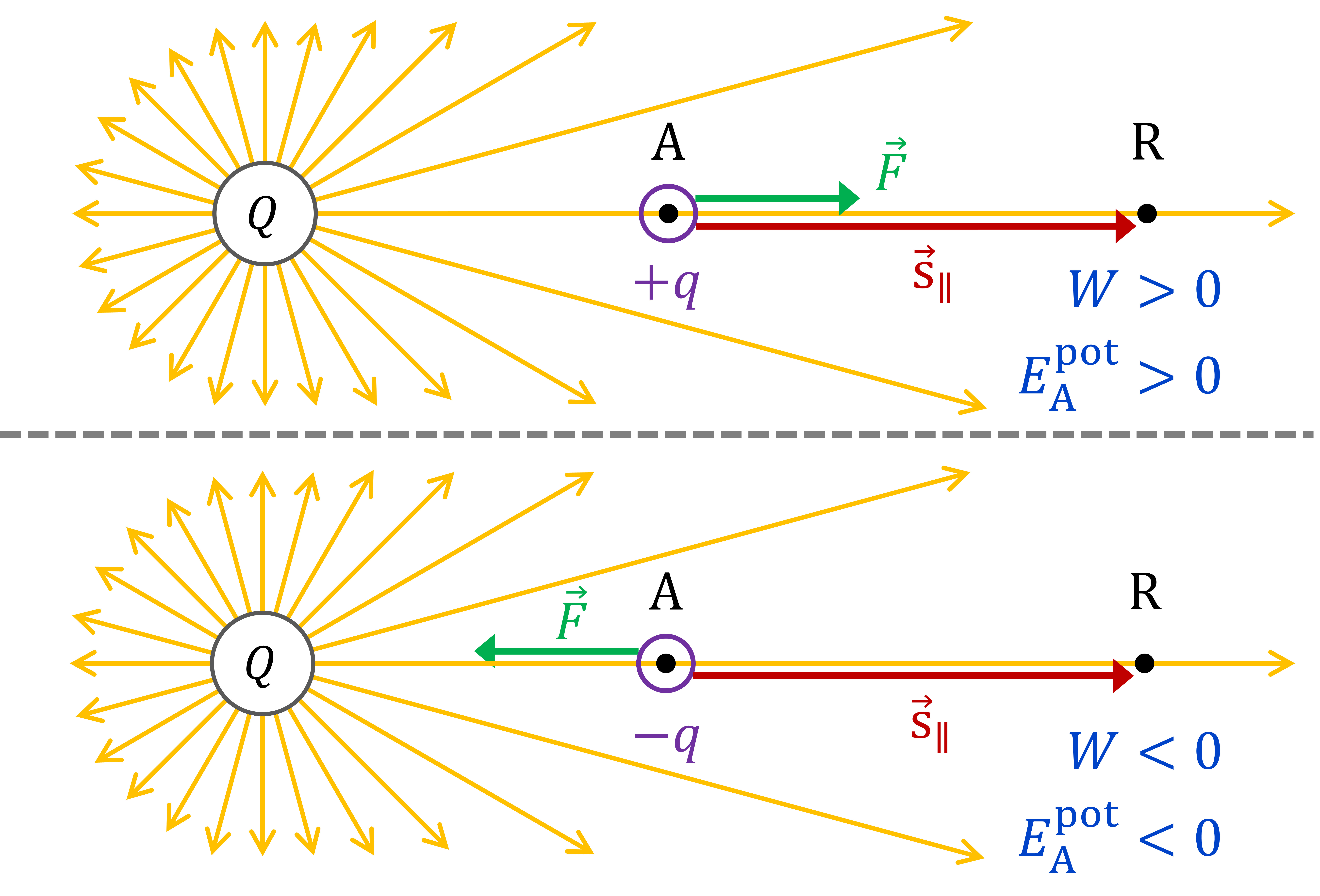
Ez alapján az 1. esetben az elektromos erő munkavégzés pozitív, ugyanis az erő is térerősség irányú és az elmozdulás is, márpedig a munka pozitív, ha az erő és a vele párhuzamos elmozduláskomponens egyirányúak. A 2. esetben az elektromos mező munkája negatív, hiszen az erővel ellentétes irányba mozgattuk a töltést. A 3. esetben pedig az elektromos mező munkája nulla, hiszen a térerősségre merőleges elmozdulás esetén az erő és az elmozdulás egymásra merőlegesek, így az elmozdulásnak nincs olyan \(s_{\parallel}\) komponense, mely az erővel párhuzamos. Ezek alapján:
Pozitív töltés potenciális energiája a térerősség irányába haladva csökken, a térerősséggel ellentétesen haladva növekszik. Negatív töltésé a térerősség irányába haladva növekszik, a térerősséggel ellentétesen haladva csökken. A térerősségre merőlegesen haladva minden töltés potenciális energiája változatlan marad.
Mivel az elektrosztatikus mező erővonalai a pozitív töltésekből indulnak ki, és a negatív töltésekben végződnek, ebből következően egy áramforrás pozitív pólusánál mindig magasabb a potenciális eneriája, mármint a pozitív töltésnek. Ha ugyanis az eddigi \(\mathrm{A}\) pontba nem pozitív \(q\) töltést helyezünk, hanem egy negatív töltést, akkor őt elmozgatva a referenciapontba, a mező munkája ellentétes előjelű lesz az eddigihez képest, hiszen a negatív töltésre ellentétes irányú erő hat, mint az eddigi pozitív töltésre.
A potenciál
Végezzünk el egy gondolatkísérletet: helyezzünk az \(\mathrm{A}\) pontba először egy pozitív \(q\), majd szintén pozitív, de 2-szer illetve 3-szor nagyobb töltést, és gondoljuk végig a potenciális energiáikat! vagyis képzeletben mozgassuk el őket az \(\mathrm{R}\) referenciapontba, és nézzük meg közeben a mező munkáját.
A 2-szer illetve 3-szor nagyobb töltésre az elmozdulás kötben mindvégig ugyanolyan irányú, csak 2-szer, 3-szor nagyobb erő hat, mint az eredeti \(q\) töltésre, így a munkavégzés is 2-szer, 3-szor nagyobb lesz. Vagyis a 2-szer 3-szor nagyobb töltésnek a potenciális energiája 2-szer, 3-szor nagyobb, tehát a potenciális energia egyenesen arányos a próbatest töltésével:
\[E^{\mathrm{pot}}_{\mathrm{A}}\sim q\]
Ha két mennyiség egyenesen arányos, akkor a hányadosuk egy állandó (konstans) érték:
\[\frac{E^{\mathrm{pot}}_{\mathrm{A}}}{q}= \mathrm{konst}\]
Ez a konstans tehát független attól, hogy mekkora töltést helyezünk oda, vagyis ez az elektromos mező \(\mathrm{A}\) pontját jellemzi. Mivel egy hányadost látunk (ami mindig "az egységnyi alsóra jutó felsőt" jelenti) ezért ez a konstans megmutatja, hogy mekkora az egységnyi töltésre jutó potenciális energia az \(\mathrm{A}\) pontban. Vagyis megmutatja, hogy mennyi az elektromos mező munkája, miközben egy egységnyi nagyságú pozitív töltés az \(\mathrm{A}\) pontból a referenciapontba mozdul el. Ezt a konstanst az \(\mathrm{A}\) pont potenciáljának hívjuk, és \(U_{\mathrm{A}}\)-val jelöljük:
\[U_{\mathrm{A}}=\frac{E^{\mathrm{pot}}_{\mathrm{A}}}{q}\]
A potenciál mértékegysége a definíciója alapján:
\[\left[U_{\mathrm{A}}\right]=\frac{\left[E^{\mathrm{pot}}_{\mathrm{A}}\right]}{\left[q\right]}\]
\[\left[U_{\mathrm{A}}\right]=\frac{\mathrm{J}}{\mathrm{C}}\]
De mivel az emberek lusták, és nem szeretnek törteket írni, ezért ezt elnevezték egy Volta nevű olasz fizikus tiszteletére \(\mathrm{volt}\)-nak, amit \(\mathrm{V}\)-vel rövidítünk:
\[\left[U_{\mathrm{A}}\right]=\mathrm{V}\]
Ekvipotenciális felületek
Amikor egy töltés a térerősségre merőlegesen mozog, akkor az elektromos mező munkája nulla, így a töltés potenciális energiája változatlan marad. Mivel a potenciál a pozitív egységtöltés potenciális energiája, ezért térerősségre merőleges elmozdulás során a potenciál is változatlan marad. Vagyis ilyenkor csupa olyan pontokba jutunk, ahol a potenciál a kiindulóponttal azonos.
Elektrosztatikus mezőben az azonos potenciálú pontok felületet alkotnak, melyet ekvipotenciálsi felületnek nevezünk. Egy ekvipotenciális felület minden pontjában merőleges a térerősségvektorra.
1. példa: homogén elektromos mező
Homogén elektromos mezőben az erővonalak egyenesek, az erre merőleges ekvipotenciális felületek pedig síkok
2. példa: centrális elektromos mező
Ilyen van például egy pontszerű töltés körül, vagy egy töltött fémgömb körül. Ilyenkor az elektromos erővonalak "sugárirányban" mindenfelé futnak, az elvipotenciális felületek pedig gömbök:
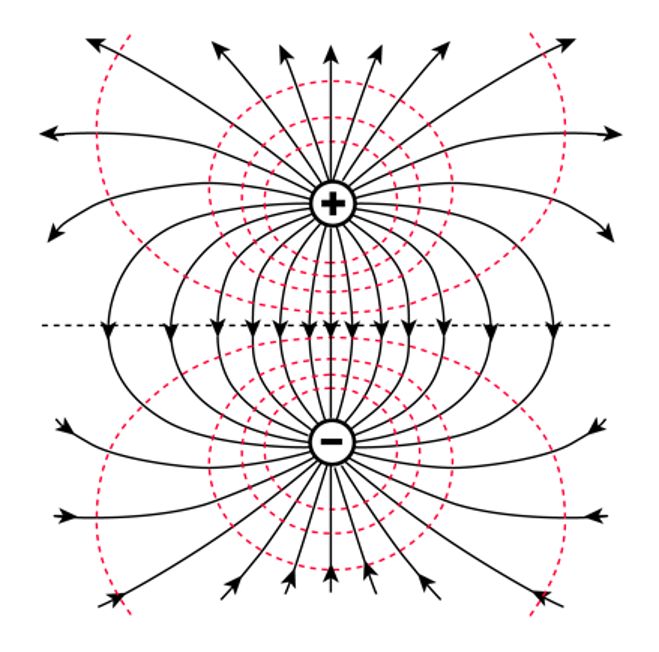
3. példa: két azonos nagyságú, ellentétes előjelű töltés egymás közelében (dipól)
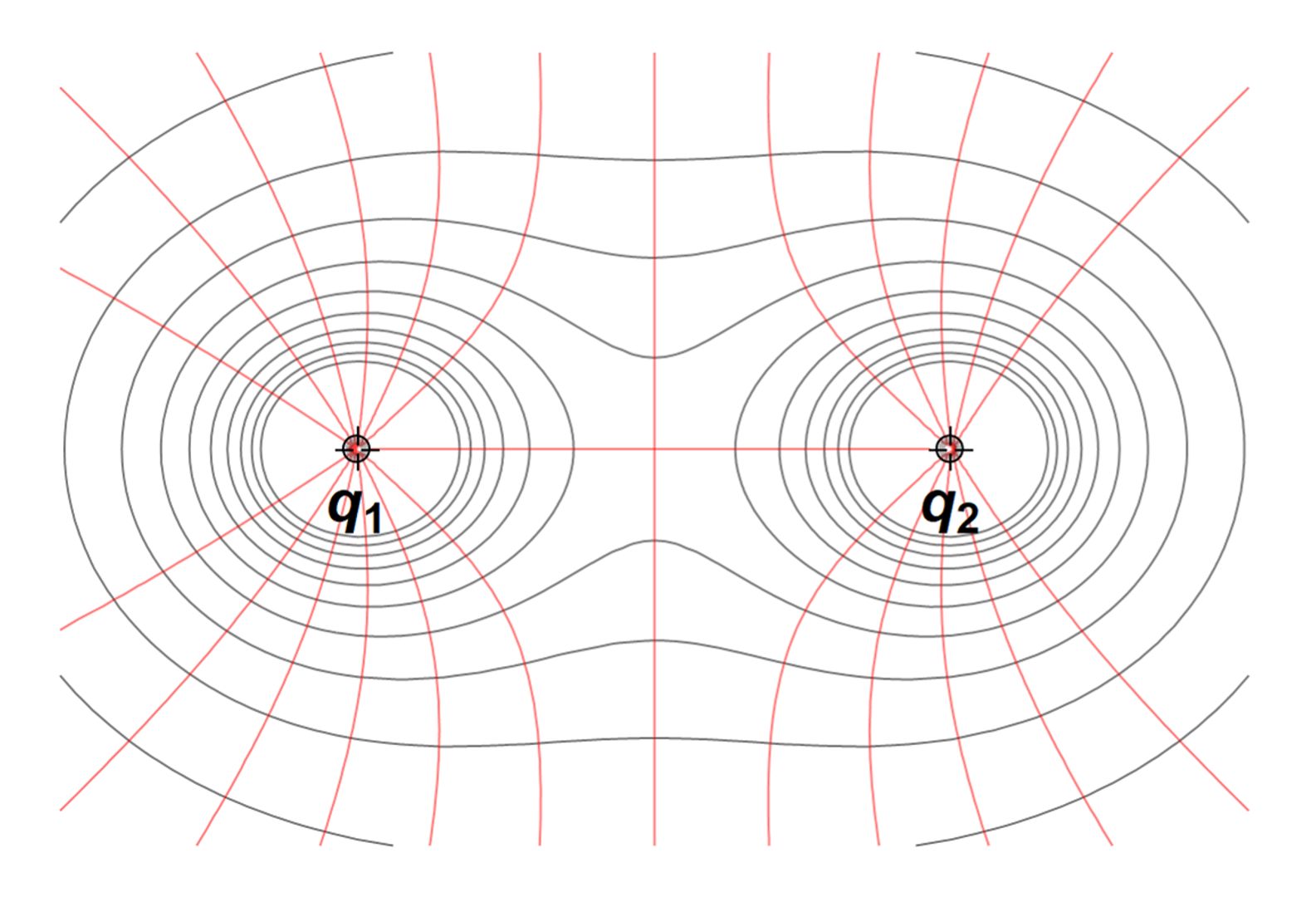
4. példa: két azonos töltés egymás közelében:
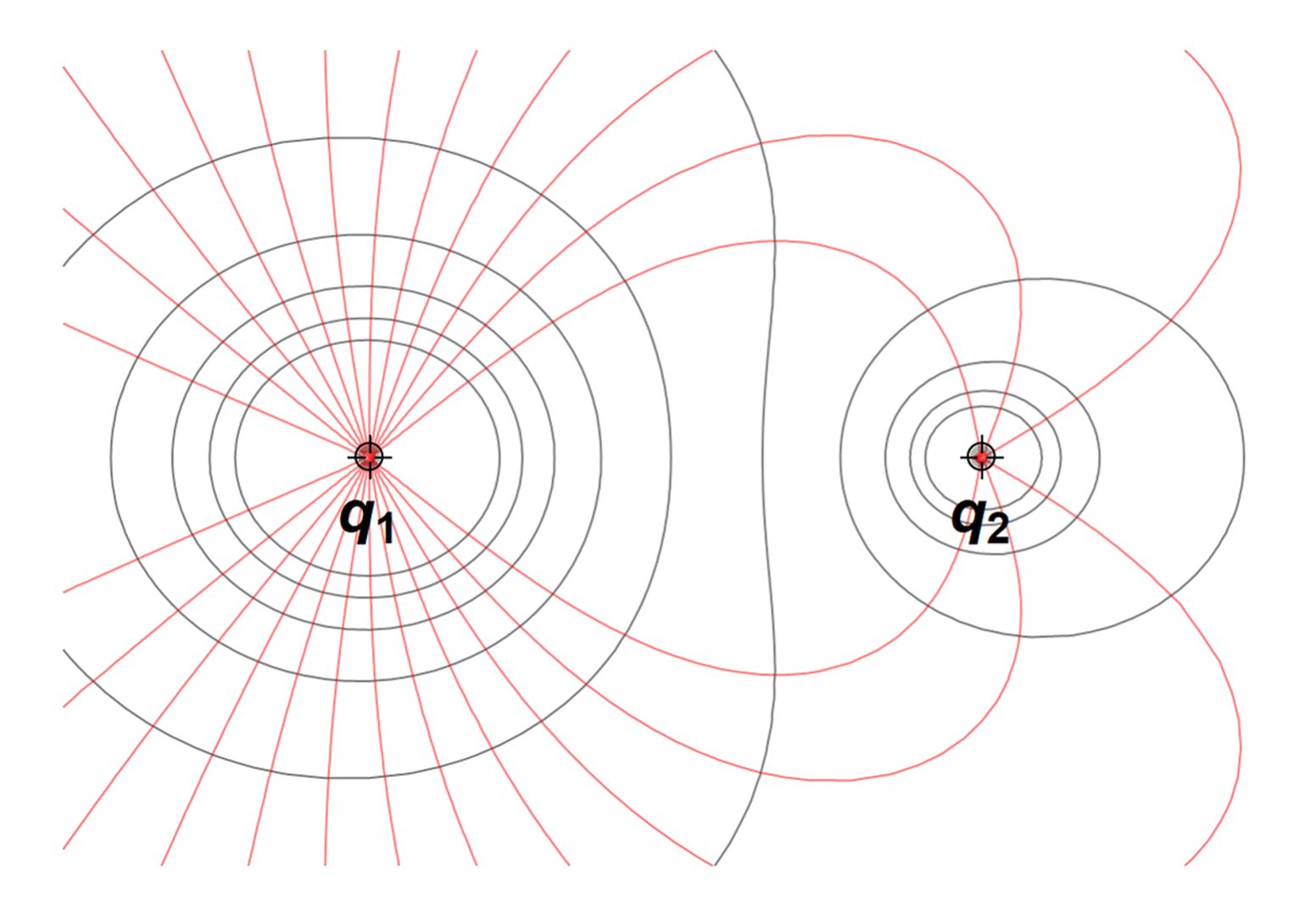
5. példa: két különböző nagyságú, ellentétes előjelű töltés egymás közelében
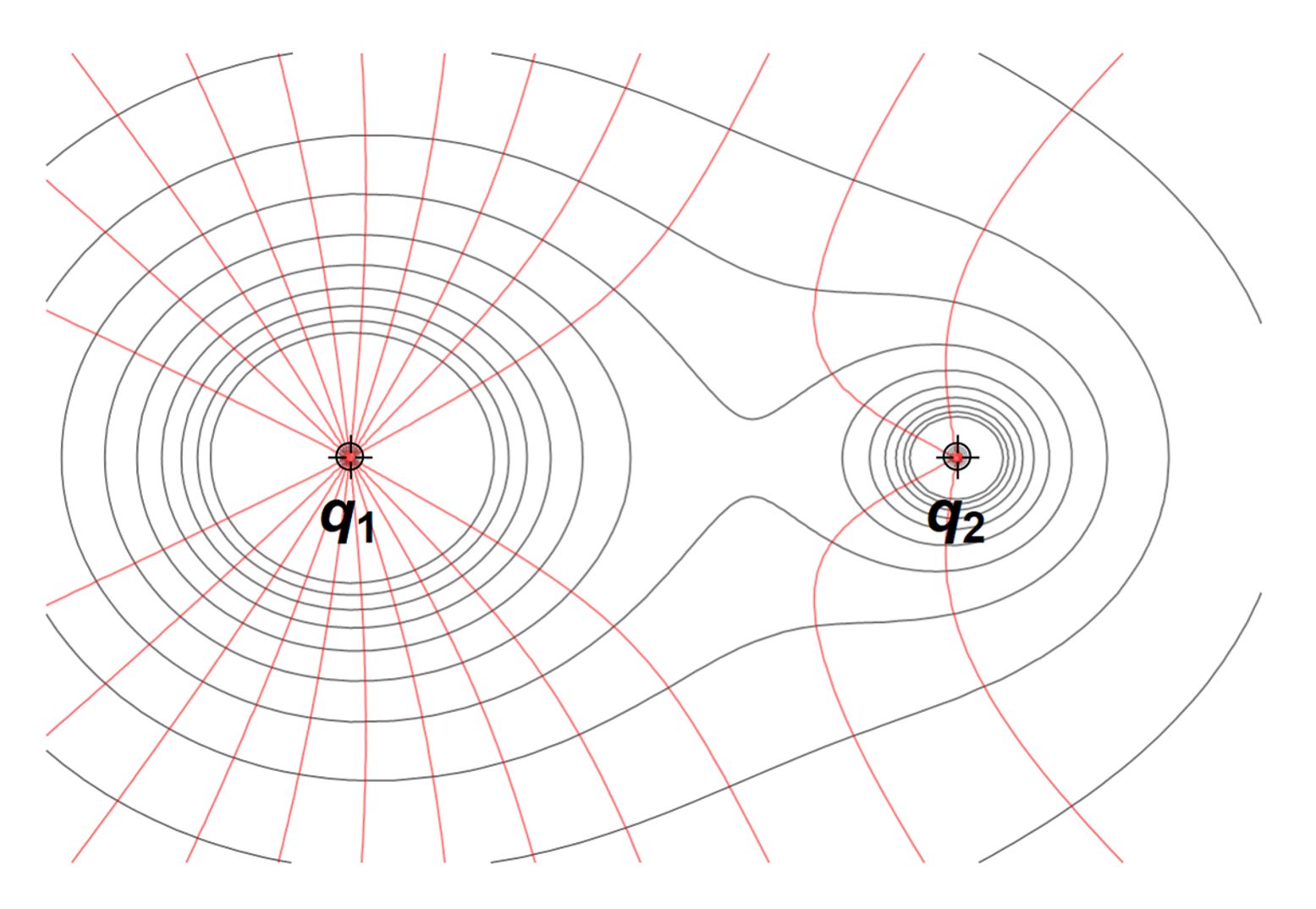
6. példa: különböző nagyságú, azonos előjelű töltések egymás közelében