Minden test (még a nagyon hidegek is) minden hőmérsékleten elektromágneses sugárzásokat bocsát ki, ezt hívjuk hőmérsékleti sugárzásnak. A kibocsátott (emittált) sugárzás sokféle frekvenciájú, hullámhosszú lehet (rádióhullám, mikrohullám, infravörös-sugárzás, látható fény, ultraibolya-sugárzás, röntgen- és gamma-sugárzás). A 19. század végén ezen elektromágneses komponensek nem is mindegyike volt ismert, ezért mérőműszerek sem álltak rendelkezésre a vizsgálatukhoz. De ez nem lehet akadálya a vizsgálódásnak, például adott idő alatt a kibocsátott sugárzás összes energiáját vizsgálhatjuk úgy, hogy azt ismert hőkapacitású testre bocsátjuk, és annak hőmérséklet-emelkedését mérve megkapjuk az elnyelődött sugárzás energiáját.
Alapfogalmak
Definiáljuk az \(e\) emisszióképességet úgy, hogy a test egységnyi felületű darabja által egységnyi idő alatt (a felületre merőleges irányban, egységnyi térszögben) kibocsátott (különféle hullámhosszúságú) elektromágneses sugárzások összes energiája. Az emisszióképességet részletezhetjük az egyes \(\lambda\) hullámhosszak szerint is, továbbá az emisszióképesség függ a \(T\) hőmérséklettől is, ezt ki szokás hangsúlyozni az alábbi függvény jelöléssel:
\[e=e(\lambda,\ T)\]
Ezután definiáljuk az \(a\) abszorpcióképességet: a test által elnyelt (abszorbeált) sugárzási energia és a testre eső sugárzási energia hányadosa, más szóval hányszorosát nyeli el a test a ráeső sugárzásnak, vagyis hányadrész az, amit nem ereszt át magán és nem ver vissza. A testek elnyelőképessége eltérhet a különböző hullámhosszakra, és akár a hőmérséklettől is függhet, ezért az abszorpcióképesség is függvénye \(\lambda\)-nak és \(T\)-nek:
\[a=a(\lambda,\ T)\]
A feketetest
Az abszorpcióképesség egyik határesete, ha egy test minden ráeső sugárzást elnyel, azaz rá nézve \(a=1\), ezt hívjuk abszolút feketetestnek, vagy röviden feketetestnek. Bár a feketetest idealizáció, a gyakorlatban jó közelítéssel megvalósítható, ha készítünk egy \(V\) térfogatú üreget, melynek belső falát (a nagyfokú fényelnyelés érdekében) feketére festjük vagy kormozzuk, és az üreg falára egy kisebb, \(A\) felületű lyukat fúrunk. Ekkor nem az üreg a feketetest, hanem a kisméretű lyuk, pontosabban szólva ez egy \(A\) felületű feketetest. A lyukra eső sugárzás ugyanis az üreg belső falán visszaverődve minimális eséllyel indul pont a lyuk irányába, szinte biztosan az üreg belső falának egy másik pontja felé fog haladni, vagyis csak a belső falon törénő sokszoros visszaverődés után "talál ki" a lyukon, amin bejött. Mivel az üreg fala fekete, ezért minden egyes visszaverődés erősen gyengíti a nyalábot (a fekete festék minimum 90%-át elnyeli a ré eső fénynek), úgyhogy mire több visszaverődés után végre "kitalálna" a lyukon, addigra már elhanyagolhatóan kicsire csökken a sugárzás erőssége.
Érdekes, hogy a sok visszaverődés miatt egy üreg falára fúrt kis lyuk már akkor is feketének látszik, ha az üreg belső fala nincs is feketére festve, hanem egyenesen fehér!
A Kirchhoff-törvény
Térjünk vissza az emisszióképesség s az abszorpcióképesség kapcsolatára. A különféle testek emisszióképessége és az abszorpcióképessége igen sokféle, eltérő érték lehet. Ezért kissé meglepő, amit Kirchhoff termodinamikai megfontolásokból 1860-ben levezetett, hogy ha a test sugárzási egyensúlyban van a környezetével, akkor az \(\displaystyle \frac{e}{a}\) hányados a test tulajdonságaitól függetlenül mindig ugyanannyi, csak a \(\lambda\) (illetve \(f\)) valamint a \(T\) függvénye:
\[\frac{e(f ,\ T)}{a(f ,\ T)}=\frac{c}{8\pi}\cdot u(f,\ T)\]
\[\frac{e(\lambda ,\ T)}{a(\lambda ,\ T)}=\frac{{\lambda}^2}{8\pi}\cdot u(\lambda,\ T)\]
Az \(u(\lambda,\ T)\) illetve \(u(f,\ T)\) függvény neve spektrális energiasűrűség, ami egy univerzális (minden testre érvényes) függvény, így érdemes lenne meghatározni, Kirchhoff-nak azonban magát a függvényt nem sikerült levezetnie. A feketetest viszont kapóra jön, hiszen az abszorpcióképessége (definíció szerint) egységnyi, így a feketetest emisszióképességét leíró \(e(\lambda,\ T)\) függvény megegyezik ezzel a keresett \(u(\lambda,\ T)\) spektrális energiasűrűség függvénnyel, és az emisszióképesség már kísérletileg vizsgálható. Tehát ha nem sikerül elméleti úton levezetni, attól még empirikusan meghatározhatjuk.
A Stefan-Boltzmann-törvény
1879-ben Stefan kísérleti úton azt találta, hogy egységnyi felületű (\(A=1\)) feketetest által kibocsátott különféle hullámhosszúságú sugárzások összteljesítménye a \(T\) abszolút (Kelvinben mért) hőmérséklet negyedik kitevőjével arányos:
\[\frac{P_{\mathrm{össz}}}{A}=\int_{0}^{\infty} u(\lambda,\ T)=\sigma T^4\]
Ezt Boltzmann 1884-ben le is vezette elméleti megfontolásokból, ezért ma már Stafan-Boltzmann-törvény a neve, a benne szereplő \(\sigma\) konstans alapvető természeti állandókból áll össze:
\[\sigma =\frac{2{\pi}^5 k^4}{15\ c^2 h^3}=5,67\cdot 10^{-8}\ \mathrm{\frac{W}{m^2\cdot K^4}}\]
Tehát a Stefan-Boltzmann-törvény az általunk keresett \(u(\lambda,\ T)\) függvény görbe alatti területét adja meg valamilyen $T$ hőmérsékleteken, de az \(u(f,\ T)\) függvény alakját továbbra sem ismerték.
A Wien-féle eltolódási törvény
A kísérletek során kiderült, hogy a függvény a frekvencia (illetve hullámhossz) szerint "púpos", azaz minden hőmérsékleten van egy olyan \(f_{\mathrm{max}}\) frekvencia (illetve egy \(\lambda_{\mathrm{max}}\) hullámhossz), melyből a legtöbbet sugároz a feketetest, és a hullámhossz tengelyen ettől távolodva (mind kicsi, mind nagy frekvenciák felé) a sugárzás intenzitása egyre kisebb. 1893-ban Wien elméleti megfontolásokból azt kapta, hogy a keresett \(u(f,\ T)\) függvényből kiemelhető egy \(f^3\) (a "frekvencia köbe") szorzótényező:
\[u\left(f,\ T\right)=f^3\cdot F\left(\frac{f}{T}\right)\]
Ebből aztán (annak segítségével, hogy a függvény maximumhelyén a derivált nulla kell legyen) levezette, hogy a maximális intenzitású hullámhossz fordítottan arányos a hőmérséklettel:
\[\lambda_{\mathrm{max}}\cdot T=\mathrm{konst.}=2,9\cdot 10^{-5}\ \mathrm{m\cdot K}\]
Ezt hívjuk Wien-féle eltolódási törvénynek. Eszerint a hőmérséklet növelésével \(\lambda_{\mathrm{max}}\) eltolódik a rövidebb hullámhosszak felé. Nagyon kis hőmérsékleten (néhány Kelvinen) leginkább mikrohullámú a hőmérsékleti sugárzás (lásd kozmikus háttérsugárzás), aztán szobahőmérsékleten már jellemzően infravörös (lásd éjjellátó infrakamera), aztán a 6000 Celsius felszíni hőmérsékletű Nap már leginkább látható fényt sugároz, a jóval forróbb csillagok pedig már ultraibolyában pompáznak.
Azonban az \(\displaystyle F\left(\frac{f}{T}\right)\) függvényt továbbra sem sikerült elméleti úton levezetni, így az \(u(f,\ T)\) függvényről csak (nem könnyű) mérésekkel lehetett ismeretekhez jutni. Mivel a különféle frekvenciatartományok eltérő műszereket igénelnek, így a teljes függvénynek egyszerre mindig csak valamely kisebb tartományát lehetett kimérni.
A Rayleigh-Jeans-törvény
Rayleigh 1900-ban megpróbálta statisztikus fizikai módszerekkel meghatározni a függvényt. Abból indult ki, hogy ha az üregben lévő sugárzás hasonló, mint a gáztartályban repkedő gázmolekulák. A sugárzástt kibocsátó atomokat harmonikus oszcillátoroknak tekintve (azaz mint egy rugóra rögzített elektromos töltés, melynek van sajátfrekvenciája, amivel tud rezegni, ilyen frekvenciájú sugárzést kibocsátani és elnyelni) az ekvipartíció tétele alapján egyensúlyban minden oszcillátor minden szabadsági fokán átlagosan
\[\varepsilon=\frac{1}{2}kT\]
energia van, vagyis a kinetikus és potenciális energia miatt minden oszcillátorra \(kT\) energia jut. A sugárzási térben pedig minden állóhullám szintén \(kT\) energiával kell rendelkezzen, mert az elektromos és mágneses mező két energiatárolási lehetőséget nyújt. Ennek eredményeként az alábbi, ún. Rayleigh-Jeans-formula adódott:
\[u(\lambda,\ T)=\frac{8\pi}{c^3}f^2\ kT\]
Ezzel az volt a gond, hogy egyre nagyobb frekvenciákon a feketetestnek eszerint egyre többet kellene sugároznia, ezért a teljes spektrumra nézve a kisugárzott összteljesítmény végtelen nagynak adódik. Mivel a végtelen sok sugárzás a nagy frekvenciájú tartomány miatt adódik, és a látható fény tartománynél au ultraibolya a nagyobb frekvenciájú tartomány, ezért a problémát Ehrenfest (hatásvadász módon) "ultraibolya-katasztrófának" nevezte el. Nyilvánvaló volt, hogy a levezetés hibás, de nem tudták, miért.
A Wien-féle sugárzási formula
Wien 1896-ban a Maxwell-féle sebességeloszlást hívta analógiaként, amiben adott mozgási energiájú gázmolekulák részaránya a növekvő sebességgel exponenciálisan csökken. Ebből kiindulva a következő formulát vezette le:
\[u(f,\ T)=c_1f^3\cdot e^{-c_2\frac{f}{T}}\]
ahol \(c_1\) és \(c_2\) konstansok, melyek úgy kell megválasztanunk, hogy a a formula a legjobb egyezést adja a mérésekkel.
Ez a függvény rögzített $T$ hőmérsékletnél a frekvencia függvényében a tapasztalattal egyezően "púpos" görbe, vagyis mind kicsi, mind nagy frekvenciáknál nullává válik. Ezzel ugyan megoldódott a Rayleigh-Jeans-féle "ultraibolya-kataszrófa", de volt egy nagy gond vele, amiből egyértelmű volt, hogy még nem ez a helyes hőmérsékletisugárzási-törvény. Ehhez át kell állítani az agyunkat, ugyais eddig arra koncentráltunk, hogy egy rögzített $T$ hőmérséklet esetén mennyit sugároz a feketetest a különféle frekvenciákból. Most az \(u(f,\ T)\) kétváltozós függvénynél képzeletben rögzítsük a frekvenciát, és nézzük meg, mennyit sugároz a feketetest ebből az adott frekvenciából különféle $T$ hőmérsékleteken! A Wien-féle sugárzási formula magas hőmérsékleten azt jósolta, hogy a feketetest emisszióképessége nem függ a hőmérséklettől.
A hőmérsékletfüggetlenséget úgy is fogalmazhatjuk, hogy hiába melegítjük a feketetestet, attől nem bocsát ki több sugárzást. Ez eleve nem volt túl hihető, aztán kíséreltileg is cáfolták: 1900-ra Rubens és Kurlbaum pontosabb mérései azt adták, hogy a kis frekvenciájú infravörös tartományban (ami megfelel a formulában a nagy hőmérsékletű esetnek) a spektrális energiasűrűség nem konstans, hanem egyenesen arányos a hőmérséklettel, ami ellent mondott a Wien-féle sugárzási formulának.
A Planck-formula
Volt tehát két formula, melyek vagy a kis, vagy a nagy frekvenciákon írták le helyesen a feketetest-sugárzást. Planck megpróbálta felírni a minden tartományban helyes formulát, de egyszerre arra is törekedett, hogy necsak matematikai bűvészkedés révén kapja meg, hanem fizikai alapjai is legyenek a levezetésnek. Ehhez a sugárzási tér entrópiáját kezdte vizsgálni, mert arra már voltak alapvető összefüggések (konkrétabban az entrópiának a belső energia szerint második deriváltját nézte). Az entrópiával azonban az volt a baj, hogy ott egy állapot \(W\) termodinamikai valószínűségét az őt megvalósító lehetséges mikroállapotok száma határozza meg, így az entrópiához ismerni kellene a lehetséges mikroállapotok számát:
\[S=k_{\mathrm{B}}\cdot \ln W\]
Csakhogy itt végtelen számú esettel volt dolgunk, hiszen az üreg falában lévő oszcillátorok végtelen sokféle frekvenciát bocsátottak ki (mivel folytonosan, azaz végtelen sűrűn voltak a lehetséges, kisugározható, elnyelhető frekvenciák).
Planck azon volt, hogy az entrópia analíziséhez a mikroállapotok számát "megszámlálhatóvá", vagyis véges mennyiségűvé tegye, ezért ennek érdekében (általa hangsúlyozottan) "tisztán matematikai segédeszközként" azzal a feltevéssel élt, hogy az üreg falában lévő (a sugárzást kibocsátó és elnyelő) oszcillátorok energiája nem lehet akármekkora, hanem csak egy kicsi \(\varepsilon\) energiaértéknek az egész számú többszöröse. Tehát egy ilyen oszcillátor energiája az n-edik állapotában:
\[E_n=n\cdot \varepsilon\]
amiből következően az általa kisugárzott (vagy elnyelt) elektromágneses hullám energiája is csak az oszcillátor lehetséges energiáinak különbsége lehet, vagyis:
\[\Delta E=n\cdot \varepsilon\]
Feltételezte továbbá, hogy egy ilyen "elektromágneses energiaadagocska" az \(f\) frekvenciával arányos:
\[\varepsilon=hf\]
Ahhoz hogy a formulája pontosan visszaadja az empirikus görbét, az itt megjelenő \(h\) arányossági tényezőt a megfelelő módon kell megválasztani. Ma ezt az Planck-állandónak hívjuk, értéke \(h=6,626\cdot 10^{-34}\ \mathrm{J\cdot s}\). Az energia·idő dimenziója alapján a klasszikus mechanika "hatás" mennyiségéhez hasonlít, ezért "hatáskvantum"-nak is nevezzük.
A fenti feltevéseken túl az ekvipartíci helyett szükség volt még a Boltzmann-elszlásra is segítségével Planck az alábbi formulát vezette le, mely már tökéletesen illeszkedett a kísérleti eredményekhez:
\[\boxed{u(f,\ T)=\frac{8\pi h}{c^3}f^3 \frac{1}{e^{\frac{hf}{kT}}-1}}\]
illetve ugyanez hullámhosszal felírva:
\[\boxed{ u(\lambda,\ T)=8\pi ch \frac{1}{{\lambda}^5} \frac{1}{e^{\frac{hc}{\lambda kT}}-1}}\]
A Planck-féle sugárzási törvénnyel tényleg összeállt minden, ugyanis a deriválásával előáll a Wien-féle eltolódási törvény, míg integrálásával a Stefan-Boltzmann-törvény.
A sugárzási törvények (Wien, Rayleigh-Jeans, Planck) összehasonlítása
A hőmérsékleti sugárzást leíró törvények kétváltozós függvények (az egyik változójuk a \(T\) hőmérséklet, a másik pedig a \(\lambda\) hullámhossz vagy az \(f\) frekvencia), ezért az ábrázolásukra két fő lehetőség van:
- ha mindkét változót figyelembe akarjuk venni, akkor felületként kellene ábrázolni
- ha csaz az egyik változó hatását akarjuk megmutatni, akkor egyszerűbb a helyzet, mert síkban (x-y koordinátarendszerben) is ábrázolhatjuk, a másik változót állandó értéken tartva
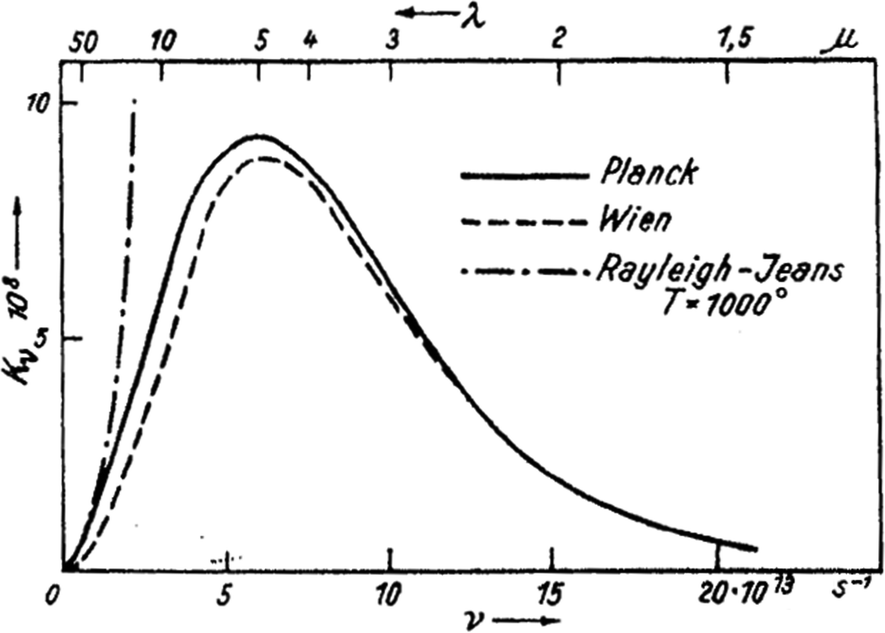
A kétváltozós, felületen történő verzió nem szokás, hanem a hőmérséklet állandósága mellett a hullámhossz illetve frekvencia változójú függvények a gyakoriak. Ezen így néznek ki a versengő sugárzási törvények (a vízszintes tengelyen a \(\nu\) a frekvencia régebbi jele, a \(K\) pedig a sugárzás fajlagos intenzitása).
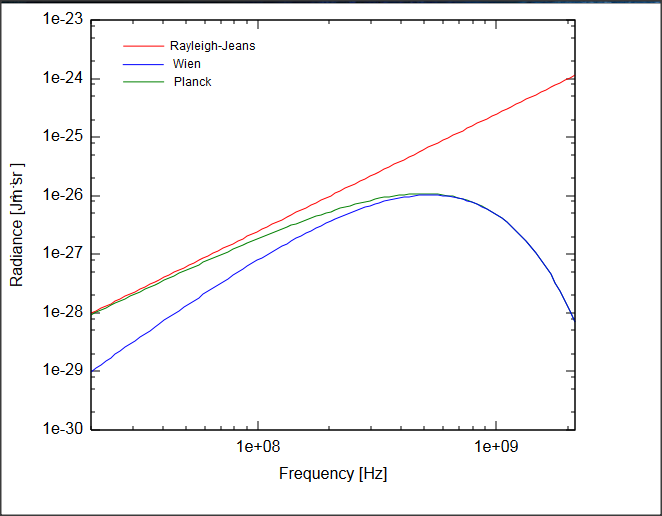
Tehát a Rayleigh-Jeans-törvény csak kis frekvenciákon (nagy hullámhosszokon) jó, máshol teljesen rossz. A Wien-féle formula frekvenciafüggése azonban minden frekvenciatartományban meglehetősen jó; csak kicsit tér el a mérésektől, melyekr a Planck-féle formula tökéletesen ileszkedik. A kis eltérést jobban láthatóvá tehetjük, ha a skálák logaritmikusak:
A Wien-féle törvénynek nem is ez a komoly problémája, az az állandónak tartott frekvencia esetén a hőmérsékletfüggést mutató grafikonon jelentkezik: itt alacsony frekvenciákon a hőmérséklet szerint konstans (vízszintes) a görbe (azaz a kibocsátott hőmérsékleti sugárzás erőssége a Wien-formula szerint itt nem függ a hőmérséklettől), míg a valóságban a hőmérséklettel egyenesen arányosságban van (minden frekvencián).
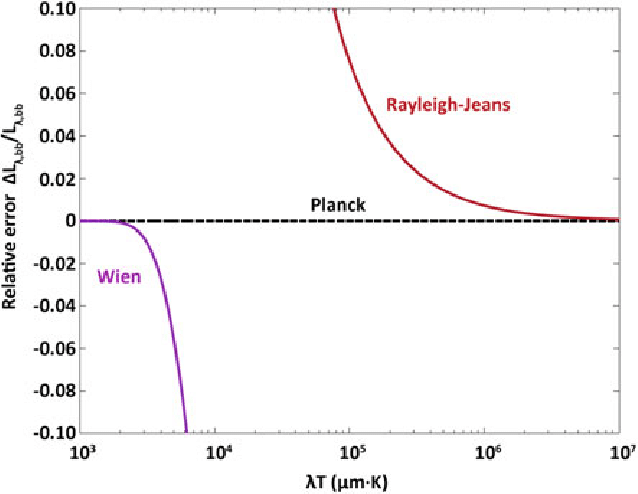
Ennek szemléltetésére szolgál, ha a vízszintes tengelyre nem a hullűmhosszot vagy a frekvenciát, hanem a \(\lambda \cdot T\) mennyiséget (a hullámhossz és a hőmérséklet szorzatát) tesszük (szintén logaritmikus skálán), a függőleges tengelyre pedig a relatív ("százalékos") eltérést a mért értékektől. Ilyenkor valóban az adódik, hogy a Wien-törvény csak alacsony hullámhosszokon (nagy fekvenciákon) jó, a Rayleigh-Jeans-törvény pedig csak nagy hullámhosszokon (alacsony frekvenciákon).
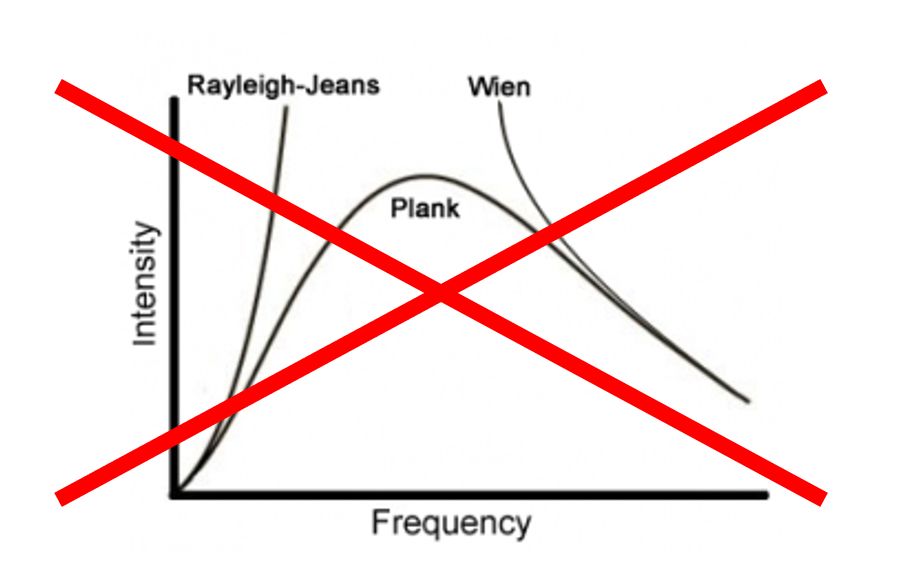
Időnként mindezt, hogy a Wien-törvénnyel baj van alacsony frekvenciákon, hibásan a szokásos frekvencia (hullámhossz) változójú grafikonon próbálják megjeleníteni:
Tudománytörténeti érdekességek
Planck oszcillátoros feltételezésével egycsapásra megszületett a kvantumelmélet, de maga Planck nem gondolta "fizikai valóságnak", hogy az elektromágneses hullámok energiája ilyen kis adagokból áll (kvantumos), hanem ezt a feltételezést csupán matematikai segédeszköznek tekintette.
Azt, hogy az elektromágneses sugárzás "kvantált" (adagos), mások is nehezen fogadták el. Einstein már 1905-ben publikálta a fotoeffektus értelmezését, melyben a fém egy elektronja mindig \(hf\) adagnyi energiát képes elnyelni az elektromágneses sugárzási térből, de csak 1921-ben kapott érte Nobel-díjat. Egy történet e két dátum közötti "félidőből", 1913-ból: Max Planck, Walter Nernst, Heinrich Rubens és Emil Warburg a Porosz Tudományos Akadémia tagjainak sorába ajánlották Einsteint, az ajánlásban a munkásságát méltató sorok mellett az is szerepelt, hogy „spekulációiban néha szeret túllőni a célon, mint például a fénykvantumhipotézisében, ezt azonban nem szabad a terhére felróni”.