Valójában két pontszerű test rugalmas ütközéseit fogjuk kivesézni.
Jelöljük úgy a mennyiségeket, hogy az egyik test (mondjuk a balról érkező) legyen az 1-es, a másik test (a jobbról érkező) pedig pedig a 2-es. Ez alapján a tömegek \(m_1\) és \(m_2\) jelűek lesznek. Továbbá az ütközés előtti sebességeket mindkét testnél jelölje \(v\) betű (azaz a kezdősebességek \(v_1\) és \(v_2\)), az ütközés utáni sebességeket pedig mindkét testnél jelölje \(u\) betű (azaz a végső sebességek \(u_1\) és \(u_2\), mert ez hasonlít a \(v\)-re, de arra is utal, hogy ezek az ütközés "utáni" sebességek, és így nem kell további indexeket használni, vagy "vesszős" mennyiségeket bevezetni).
Az ábrán a sebességvektorok irányait nem kell komolyan venni, hiszen a tárgyalásunk teljesen általános lesz, vagyis nemcsak olyan eseteket fed majd le, amikor a földi megfigyelő szerint kezdetben a testek =balról és jobbról" közelítenek egynáshoz, hanem például azt is, amikor az egyik test "üldözi" a másikat, míg utoléri. Ugyanígy az ütközlés utáni sebességvektorok irányát sem kell komolyan venni, hiszen jól tudjuk, hogy ütközés után nem feltétlenül "ugranak szét" a testek (gondoljunk az ember testébe illetve homokzsákba befúródó, és abban megálló piszolygolyóra, vagy a gépjármű szélvédőjével ütköző, és a jármű sebességét "átvevő" szúnyogra). A sebességvektorok irányát a sebesség előjele határozza meg: a pozitív érték azt jelenti, hogy az általunk választott pozitív iránnyal megegyező irányú, a negatív pedig azzal ellentétest.
Tekintsük adottnak az \(m_1\) és \(m_2\) tömegeket, valamint a kezdeti \(v_1\) illetve \(v_2\) kezdeti sebességeket, és próbáljuk meg ezekkel kifejezni az ütközés utáni \(u_1\) illetve \(u_2\) végső sebességeket!
Rugalmas ütközésben nemcsak a rendszer összes lendülete, hanem az összes mozgási energiája is megmarad. Írjuk fel először a teljes lendület megmaradását:
\[m_1v_1+m_2v_2=m_1u_1+m_2u_2\]
Ezt rendezzük is át úgy, hogy az azonos tömegek azonos oldalon legyenek:
\[m_1v_1-m_1u_1=m_2u_2-m_2v_2\]
Emeljük ki a tömegeket:
\[m_1(v_1-u_1)=m_2(u_2-v_2) \tag{1}\]
Írjuk fel az összes mozgási energia megmaradását:
\[\frac{1}{2}m_1v_1^2+\frac{1}{2}m_2v_2^2=\frac{1}{2}m_1u_1^2+\frac{1}{2}m_2u_2^2\]
Szorozzuk meg az egyenletet 2-vel:
\[m_1v_1^2+m_2v_2^2=m_1u_1^2+m_2u_2^2\]
és itt is vigyük az azonos tömegeket tartalmazó tagokat egy oldalra, majd emeljük ki a tömegeket:
\[m_1v_1^2-m_1u_1^2=m_2u_2^2-m_2v_2^2\]
\[m_1(v_1^2-u_1^2)=m_2(u_2^2-v_2^2) \tag{2}\]
Osszuk el ezt a \((2)\)-es egyenletet a lendületmegmaradásból kapott \((1)\)-es egyenlettel:
\[\frac{m_1(v_1^2-u_1^2)}{m_1(v_1-u_1)}=\frac{m_2(u_2^2-v_2^2)}{m_2(u_2-v_2)}\]
A tömegek kiesnek:
\[\frac{v_1^2-u_1^2}{v_1-u_1}=\frac{u_2^2-v_2^2}{u_2-v_2}\]
A számlálóban felhasználjuk, hogy
\[a^2-b^2=(a+b)\cdot (a-b)\]
\[\frac{\left(v_1+u_1\right)\cdot \left(v_1-u_1\right)}{v_1-u_1}=\frac{\left(u_2+v_2\right)\cdot \left(u_2-v_2\right)}{u_2-v_2}\]
Egyszerűsítés után:
\[v_1+u_1=u_2+v_2\]
\[v_1-v_2=u_2-u_1 \tag{3}\]
(Eszerint a két test relatív sebessége nem változik meg rugalmas ütközésben, hanem "megmarad". Ennek a rugalmatlan ütközéseknél legy majd jelentősége.)
Fejezzük ki ebből az egyenletből a két ismeretlen (\(u_1\) és \(u_2\)) közül az egyiket, mondjuk az \(u_2\) sebességet:
\[u_2=v_1+u_1-v_2\]
és helyettesítsük be a lendületmegmaradásból fent kapott egyenletbe:
\[m_1(v_1-u_1)=m_2(u_2-v_2)\]
\[m_1(v_1-u_1)=m_2(v_1+u_1-v_2-v_2)\]
\[m_1v_1-m_1u_1=m_2v_1+m_2u_1-2m_2v_2\]
\[(m_1-m_2)v_1+2m_2v_2=(m_1+m_2)u_1\]
\[\boxed{u_1=\frac{2m_2}{m_1+m_2}v_2+\frac{m_1-m_2}{m_1+m_2}v_1}\]
Ehhez hasonlóan levezetve a másik ismeretlen sebességre ez adódik:
\[\boxed{u_2=\frac{2m_1}{m_1+m_2}v_1+\frac{m_2-m_1}{m_1+m_2}v_2}\]
Feltűnhet, hogy az \(u_1\) és \(u_2\) ismeretlenekre kapott formulák kísértetiesen hasonlítanak egymásra. Ez, ha belegondolunk, érthető is, hiszen az elején sehogy se volt megkülönböztetve az egyik test a másiktól (túl azon, hogy az egyiket 1-esnek, a másik a 2-esnek tituláltuk), emiatt a két képlet csupán abban különbözik, hogy az 1-es illetve 2-es alsó indexek fel vannak cserélve bennük.
Az alábbiakban megvizsgáljuk ezeket néhány speciális esetben (bizonyos tömegarány és bizonyos kezdősebességek esetén).
1. spec.: Álló céltárgy, azonos tömegek
A kiindulási feltevéseink matematikai megfogalmazása:
\[m_1=m_2=m\]
\[v_2=0\]
Ilyen például, amikor egy álló billiárdgolyónak nekiütközik egy vele azonos tömegű másik billiárdgolyó (centrálisan). Helyettesítsük be ezeket a specialitásokat az általános megoldásba:
\[u_1=\frac{2m_2}{m_1+m_2}v_2+\frac{m_1-m_2}{m_1+m_2}v_1\]
\[u_1=\frac{2m}{m+m}\cdot 0+\frac{m-m}{m+m}v_1\]
\[u_1=0+\frac{0}{2m}v_1\]
\[u_1=0\]
A "bombázó" golyó végsebessége:
\[u_2=\frac{2m_1}{m_1+m_2}v_1+\frac{m_2-m_1}{m_1+m_2}v_2\]
\[u_2=\frac{2m}{m+m}v_1+\frac{m-m}{m+m}v_2\]
\[u_2=\frac{2m}{2m}v_1+\frac{0}{m+m}v_2\]
\[u_2=v_1\]
Vagyis a "bombázó" billiárdgolyó teljesen megáll, a kezdetben álló pedig átveszi a bombázó sebességét. Úgy is hívják ezt, hogy "sebességcsere", amit a slow-mo kameráknak hála meg is nézhetünk lassítva.
Nemcsak billiárdgolyók tudják ezt, hanem a profik is, ha mindent beleadnak...
2. spec.: Falnak ütköző test rugalmas ütközése
A fal az ütközéskor nem mozdul el, ami azt jelenti, hogy a neki ütköző test által rá ható erő lényegében nulla gyorsulást okoz a falon. Ez az
\[F=m\cdot a\]
Newton II. törvény szerint akkor lehetséges, ha a test \(m\) tömege végtelen nagy. Legyen a "bombázó" részecske az \(m_1\) tömegű, ekkor:
\[m_2=\infty\]
A fal kezdetben (is) áll, így:
\[v_2=0\]
Írjuk be a fenti specialitásokat az általános egyenletbe:
\[u_1=\frac{2m_2}{m_1+m_2}v_2+\frac{m_1-m_2}{m_1+m_2}v_1\]
\[u_1=\frac{2m_2}{m_1+m_2}\cdot 0+\frac{m_1-m_2}{m_1+m_2}v_1\]
\[u_1=\frac{m_1-m_2}{m_1+m_2}v_1\]
A jobb oldalon a nevezőben is és a számlálójában is az van, hogy a végtelen nagy \(m_2\) mellett az \(m_1\) elhanyagolhatóan kicsi, így elhagyható:
\[u_1=\frac{-m_2}{m_2}v_1\]
\[u_1=-v_1\]
Azt kaptuk, hogy a fallal rugalmasan ütköző test az eredeti nagyságú sebességével pattan vissza, ahogy ezt a mindennapi tapasztalatainkból is tudjuk. ersze a valóságban makroszkopikus testeknél mindig van (nem is olyan kevés) disszipáció, például még egy jó keményre fújt labda, ha a földre ejtjük, nem jut vissza az eredeti magasságába, csak annak mondjuk 70%-ára.
Egy furcsaság
A bombázó részecske impulzusa (lendülete) megváltozott, tehát a partnere (a fal) át kellett, hogy vegyen tőle valamennyi impulzust, ugyanakkor a fal mozgási energiája a kezdetivel azonos maradt,. Hogyan lehetséges, hogy "a fal impulzust átvett, viszont mozgási energiát nem"? Ennek hátterében az áll, hogy a mozgási energia "erősebben" függ a sebességtől (annak négyzetével arányos), mint a lendület (ami "csak" a sebességgel arányos). A lendületmegmaradás alapján a fal a nagy tömege miatt csak kis sebességre tesz szert (amit nem érzékelünk), a mozgási energiájában pedig ennek a nagyon kicsi sebességnek a négyzete szerepel, ami azt jelenti, hogy a fal mozgási energiája még ehhez képest is nagyon kicsi lesz.
3. spec.: Azonos tömegű, azonos sebességgel szembetalálkozó testek
A specialitásaink matematikai formában:
\[m_1=m_2=m\]
\[v_1=v\]
\[v_2=-v\]
Ezeket beírva az általános egyenletbe:
\[u_1=\frac{2m_2}{m_1+m_2}v_2+\frac{m_1-m_2}{m_1+m_2}v_1\]
\[u_1=\frac{2m}{m+m}(-v)+\frac{m-m}{m+m}v\]
\[u_1=\frac{2m}{2m}(-v)+\frac{0}{m+m}v\]
\[u_1=-v\]
Tehát a testek a kezdeti sebességükkel azonos nagyságú sebességgel pattannak vissza:
4. spec.: Azonos sebességgel szembetalálkozó testek rugalmas ütközésekor hogyan lehetséges, hogy az egyik megálljon?
A testek sebessége azonos, de szemben érkeznek, ezért:
\[v_1=v\]
\[v_2=-v\]
A tömegeik viszont nem lehetnek azonosak, hiszen ez az előző speciális esetben volt, és akkor "szétlökődtek" a kezdeti sebességükkel. Tehát biztos, hogy
\[m_1\neq m_2\]
Legyen az 1-es test, amelyik az ütközés után megáll:
\[u_1=0\]
Írjuk be ezeket a specialitásokat az általános egyenletbe:
\[u_1=\frac{2m_2}{m_1+m_2}v_2+\frac{m_1-m_2}{m_1+m_2}v_1\]
\[0=\frac{2m_2}{m_1+m_2}(-v)+\frac{m_1-m_2}{m_1+m_2}v\]
\[\frac{2m_2}{m_1+m_2}v=\frac{m_1-m_2}{m_1+m_2}v\]
\[2m_2=m_1-m_2\]
\[m_1=3m_2\]
Tehát ha \(1:3\) a tömegarány, akkor azonos sebességgel összeütközve a nagyobb tömegű meg fog állni.
5. spec.: Az eredeti sebessége hányszorosára gyorsulhat fel egy test ha azonos sebességgel szembetalálkozik egy másikkal?
Ha szembe jönnek, azonos sebességgel, akkor
\[v_1=v\]
\[v_2=-v\]
Nézzük meg, milyen esetben lesz a lehető legnagyobb mondjuk az 1-es végsebessége, azaz az \(u_1\)!
\[u_1=\frac{2m_2}{m_1+m_2}v_2+\frac{m_1-m_2}{m_1+m_2}v_1\]
\[u_1=\frac{2m_2}{m_1+m_2}\cdot (-v)+\frac{m_1-m_2}{m_1+m_2}\cdot v\]
\[u_1=\frac{-2m_2}{m_1+m_2}v+\frac{m_1-m_2}{m_1+m_2}v\]
Összevonás után:
\[u_1=\frac{m_1-3m_2}{m_1+m_2}v\]
Az egyszerűség kedvéért válasszuk meg a tömeg mértékegységét úgy, hogy az \(m_2\) egységnyi tömegű legyen, a másik tömeg pedig legyen egyszerűen \(m\):
\[u_1=\frac{m-3}{m+1}v\]
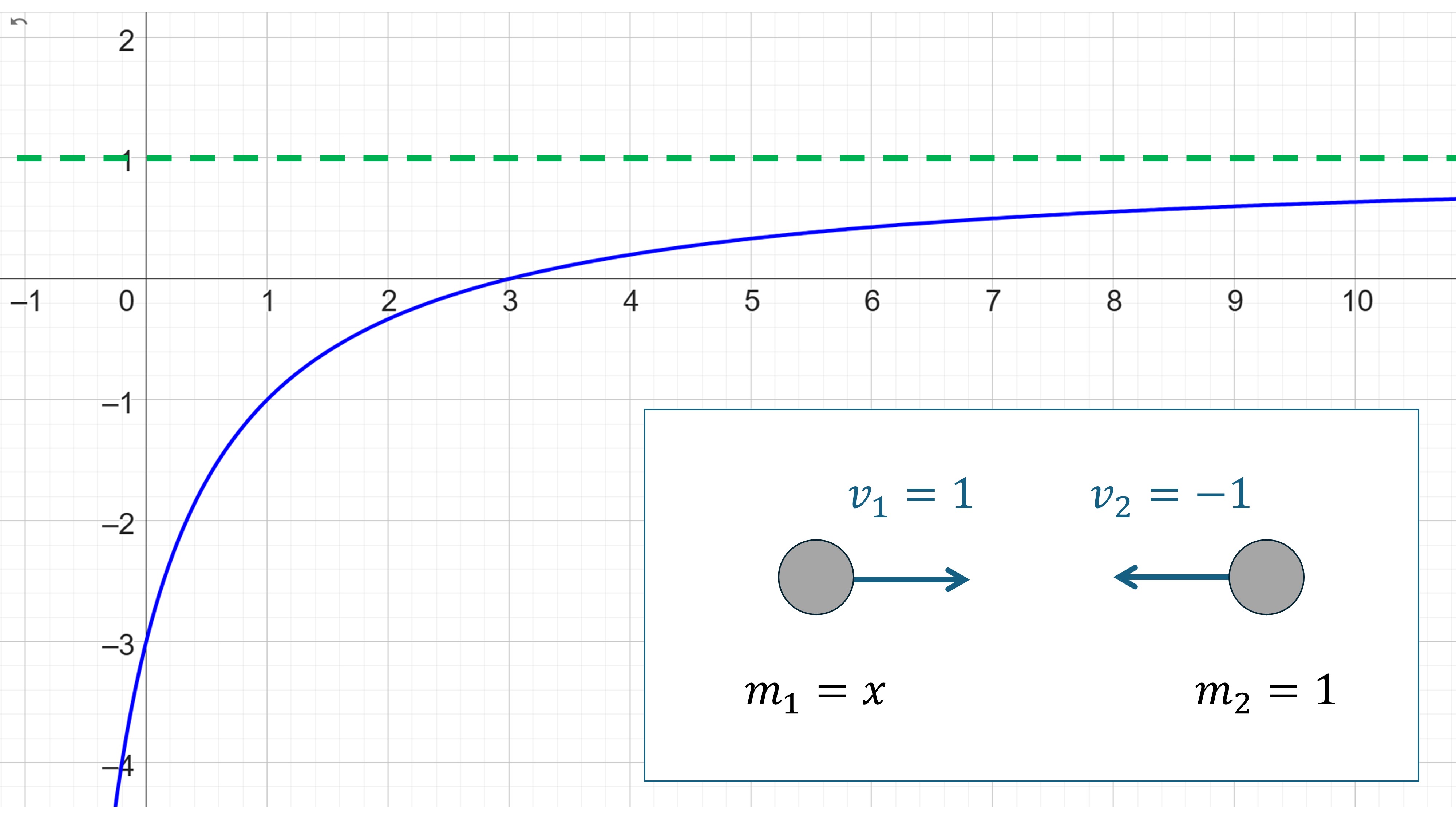
Mi a jobb oldai kifejezésnek a legnagyobb abszolút értékű, de negatív előjelű szélsőértékét keressük. Amiatt negatívot, mert azt szeretnénk, hogy a test visszapattanjon a másikról, azaz az eredeti sebességéhez képest ellentétes irányúra változzon a sebessége. Ezt valamelyik függvényábrázolóba (GeoGebra, WolframAlpha, Desmos) beírva:
azt kapjuk, hogy ennek a legnagyobb abszolút értékű negatív helye az \(m=0\) esetnél van, ekkor pedig a kialakuló maximális sebesség:
\[u_1=-3v\]
vagyis leggyorsabban a "végtelenül" kicsi tömegű testünk fog visszapattanni, méghozzá a kezdeti sebességének háromszorosával. (Természetesen az$m=\infty$ eset ugyanez, hiszen ekkor is az egyik test tömege végtelenszer nagyobb a másikénál, csak fordított szereposztással.)
Hogyan lehet ezt kivitelezni? Ha fogunk egy nagyobb tömegű golyót (pl. kosárlabda), ráhelyezünk egy jóval kisebb tömegűt (pl. goldlabda, teniszlabda, kis tömör gumilabda) és kezdősebesség nélkül leejtjük őket. Ekkor a zuhanás során súlytalanság állapotában lesznek, azaz nem nyomják egymást, de kezdetben kissé ránehezedett a felső az alatta lévőre, amitől kezdetben volt egy kis deformációjuk. A szabadesés során a kezdeti deformáció megszűnik ("relaxálódik"), ami kissé eltávolítja őket egymástól (még ha ezt szabad szemmel nem is látjuk). Így az alsó kicsit korábban ér a talajra, és ha elég gyorsan lezajlik a padlóról visszapattanása, és eléggé rugalmas, akkor már a becsapódás sebességével indul el felfelé, amikor majd "szembe találkozik" a felette lévő, zuhanó mások golyóval. Tehát nagyjából teljesül, hogy azonos nagyságú, de ellentétes irányú sebességekkel ütköznek egymásnak. Az iménti levezetés szerint ha a fenti golyó tömege jóval kisebb, mint az alsó golyó tömege, akkor közel háromszoros sebességgel fogja "fellőni" a nagy alsó a kicsi felsőt. Ezt kivitelezhetjük úgy, hogy az alsó egy (nehezebb) kosárlabda, a felső pedig egy kicsi, tömör gumilabda vagy pingponglabda. Ekkor közel 3-szoros sebességgel felfelé elindulva
\[\frac{1}{2}mv^2=mgh\]
alapján elvileg 9-szer magasabbra repülne fel, mint ahonnan elejtettük. Természetesen a valóságban az alsó labda a talajjal ütközés után kisebb sebességgel indul felfelé, mint amennyivel elérte a talajt, és a szembetalálkozáskor sem tökéletesen rugalmas az ütközés, így a 9-szeres magasság csak egy elérhetetlen elméleti határ. De van, akinek már ennek töredéke is sokkoló:
2020-ban kosárlabdával és sörrel TikTok-őrület lett ugyanebből Basketball Beer Challenge néven: