A Rutherford-féle aranyfóliás kísérlet

 Előzmény 

Thomson az elektron 1897-es felfedezését követően 1904-ben megalkotta atommodelljét, melyben az atom egy pozitív töltésű gömb ("kalács"), amiben, illetve aminek felületén találhatók a negatív töltésű, kisebb méretű elektronok, a "mazsolák". Akkoriban az atomok méretének nagyságrendjét már tudták, ami \(10^{-10}\ \mathrm{m}\). Ha az atom pozitív golyójához közel halad el egy pozitív töltésű részecske, akkor az elektromos taszítás miatt a pályája elgörbül, azaz a bombázó töltés irányt vált; a külső szemlélő számára "szóródik", még akkor is, ha nem találkoztak, nem ütköztek össze. Akkoriban vált ismertté, hogy a radioaktív \(\alpha\)-sugárzás pozitív töltésű részecskéi a hidrogénatom tömegénél 4-szer nehezebbek. Az elektrodinamikából levezethető, hogy ha egy ismert töltésű, tömegű és sebességő bombázó részecske (amilyen a radioakít alfa-részecske) egy ismert sugarú és töltésű részecske széle felé haladva eltérül, akkor az eltérülés mekkora \(\theta\) szögű lesz:

Kínálta magát, hogy egy efféle "szóráskísérlettel" próbáljunk az atom pozitív "kalácsáról" információhoz jutni. A gond az volt, hogy az alfa-sugárzás igencsak könnyen elnyelődött, már pár ceniméter levegőréteg, vagy egy vékony papírlap is teljesen elnyelte. Hát akkor az alfa-részecske repüljön vákuumban, és vegyünk valami nagyon vékony ráteget. Akkoriban az arany volt, amit nagyon vékony fóliává tudtak kalapálni: \(0,21\ \mathrm{\mu m}=210\ \mathrm{nm}\) vastagságú (kb. 1400 aranyatom vastag) hártyává (ez egyébként annyira nyelte csak el a sugárzást, mint \(1\ \mathrm{mm}\) vastag levegőréteg). Ennyire vékony fólián már az alfa-részecskék nagy része áthatolt, de ígéretesnek mutatkozott, hogy mérjük ki pontosan, hogy a bombázó részecskék hány %-a térül el adott szöggel, miután a céltárgy (target) vékony fólián áthaladt. Sok, különféle anyagú (arany, ezüst, réz, platina, ón, alumínium) és vastagságú fóliával kísérleteztek. A sugárforrás aktivitása \(30...80\ \mathrm{millicurie}\approx 1...3\ \mathrm{GBq}\) volt, azaz ból jövő alfa-részecske sebességét is sikerült kimérni, ami \(\displaystyle 2\cdot 10^7\ \mathrm{\frac{m}{s}}\)-nak adódott (a fénysebesség 6,7%-a).       
 

 A kísérleti berendezés 

Kis üvegcsőben radioaktív radon gáz volt az alfa-sugárforrás (amit korábban rádiumból állítottak elő). Ebből az őt körülvevő ólom árnyékolásra fúrt pici lyukkal egy vékony nyalábot engedtek ki, rá az aranyfóliára, mely körül körbeforgathatóan egy mikroszkóp helyezkedette el, aminek elejére \(\mathrm{ZnS}\) cink-szulfid lemezt erősítettek, ez ugyanis minden egyes becsapódó alfa-részecskétől felvillant (szcintilláció). Mindez felülnézetben:

Oldalnézetben:

Mivel az alpha-részecskéket pár centiméter levegő már elnyeli, az egész kamrából kiszivattyúzták vákuumgéppel a levegőt. A kis berendezés vázlatosan így nézett ki:

A kísérletezés éveken át tartott, és besötétített szobában kellett meredten bámulni a mikroszkóp lencséjébe, és a sötétben minden felvillanáskor húzogatni a strigulákat. Nem véletlen, hogy az idejét ezzel töltő Geiger elhatározta, gépesíteni kell ezt a szörnyű melót, ebből született később a Geiger-Müller-féle számlálócső (angol nyelvterületen Geiger counter).       
 

 Az eredmény 

Utólag nehéz az akkori fejekkel gondolkodnunk, hiszen mi már óvodás korunk óta tudjuk, hogy az atomok közepén egy 100 000‑szer kisebb méretű atommag nevű pici golyóba van sűrítve az atom tömegének elsöpró többsége. De ezt a kísérlet elején még nem tudták. Egyszerűen az volt a célkitűzés, hogy az alfa-rsézecskékkel "átvilágított" aranyatomok belső szerkezetéről valami információt nyerjenek a "bombázó" alfa-rsézecskék eltérüléseinek, "szóródásainak" tanulmányozásával. A várakozásoknak megfelelően az aranyfólián áthaladó alfa-részecskék legnagyobb része irányváltás nélkül haladt át az aranyfólián. De néha voltak oldalirányban eltérülő alfa-részecskék is. Részletesen kimérték, hogy különféle $\theta$ eltérülési szögeket az alfa-részecskék mekkora része szenved el, a relatív intenzitás szögfüggése

$$I\sim \frac{1}{\displaystyle \sin^4 \left(\frac{\theta}{2}\right)}$$

Az eredmény pont olyan, amit a centrális, taszító elektromos mező levezetésével kaphatunk. Egy konkrét szögnyi eltérülést szenvedő részecskék aránya nulla, hiszen végtelen sok lehetséges szög létezik. Valójában egy kis szögtartományba eltérült részecskéket tudunk mérni, és grafikonon az eredmény így néz ki::

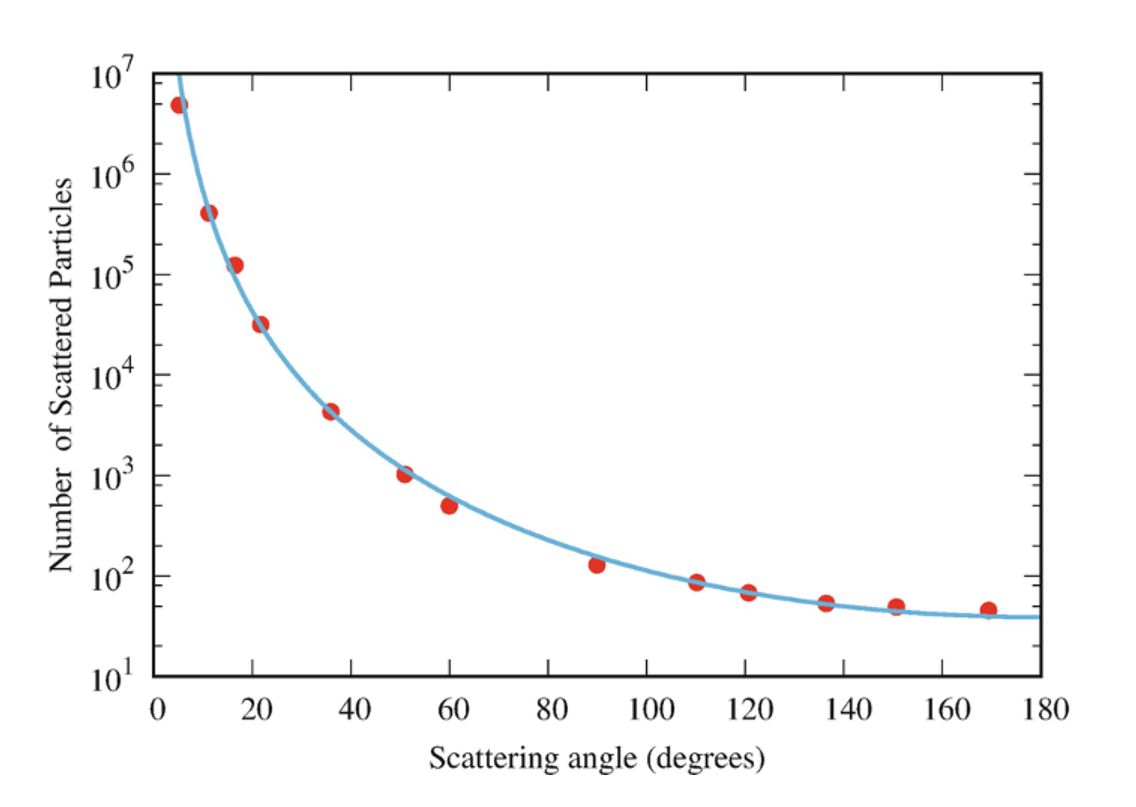
Látható, hogy a 180 fok körüli, ún. visszapattanó részecskék igen ritkák, több tízezer alfa-részecskéből csak egy fog visszapattanni. Az aranyatommag sugara $7\ \mathrm{fm}$, az $5\ \mathrm{MeV}$ energiájú alfa-részecskék maximálisan $45,5\ \mathrm{fm}$ mértékben közelítik meg az aranymag középpontját:

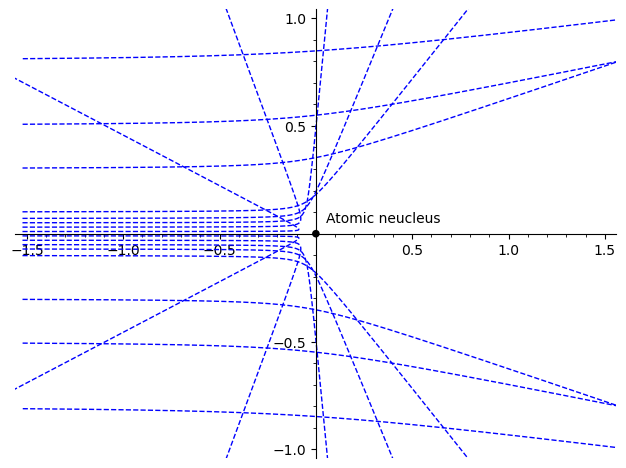
A fenti képet nézve azt gondolhatjuk, hogy "szinte minden alfa-részecske eltérül". Csakhogy az atommag 100 000‑szer kisebb, mint az atom, így a kép csak az atom nagyon kicsi középső részét mutatja. Az alfa-részecskék elsöprő többsége a képen szereplőknél sokkal (akár tízezerszer) messzebb repül el az atommag mellett, ezért azokat szinte semennyire nem téríti el az atommag taszítása.

Az ütközések tanulmányozásánál láttuk, hogy visszapattanás csak akkor lehetséges, ha a bombázó részecske kisebb tömegű annál, amit eltalál. Ez furcsa volt, hiszen az alfa-sugárzásról akkoriban már tudták, hogy héliumiont jelent, vagyis ennél nagyobb tömegű kell legyen az aranyatomban található valami, amiről visszapattant. Másrészt a Thomson-modellben az atom pozitív töltése "szét van kenve" az atomon belül, csakhogy egy ilyen "nagy méretű" pozitív töltés körül nem annyira erős az elektromos mező, hogy képes legyen az alfa-részecskét a hatalmas sebességéről lelassítani és visszalökni. Ez csak úgy lehetséges (mutatták a számítások), ha az aranyatomban lévő pozitív valami nagyon kicsi méretű. Ekkor ugyanis a belőle kiinduló elektromos erővonalak a közvetlen közelében kis felületen oszlanak el, így az erővonalsűrűséggel azonos $E$ elektromos térerősség nagy tud lenni, ami az alfa-részecskére nagy $F=E\cdot Q$ erőt tud kifejteni, ami a mozgó alfa-részecskén nagy $W=F\cdot s_{\bot}$ munkát tud végezni, hogy megállítsa és visszalökje. A számítások azt adták, hogy az aranyatomban lévő, pozitív töltésű "szórócentrum" az atomnál nagyságrendileg 100 000‑szer kisebb kell legyen, pedig az atom szinte teljes tömege ebben a picinyke golyóban van. Az atomban található, kicsiny, pozitív töltésű részt (a latin nucleus = mag) szó nyomán atommagnak nevezték el.