Coriolis francia fizikus (ejtsd: koriolisz) 1835-ben publikálta cikkét, melyben levezette, hogy ha egy vonatkoztatási rendszer az inerciarendszerekhez képest forog \(\vec{\omega}\) szögsebességgel, akkor a benne \(\vec{v}\) sebességgel mozgó test esetében fellép egy tehetetlenségi erő, melyet később róla Coriolis-erőnek neveztek el:
\[\vec{F}_{\mathrm{Cor}}=2m\left(\vec{v}\times \vec{\omega}\right)\]
amiben a jobb oldalon vektoriális szorzás szerepel, vagyis a Coriolis-erő nagysága, ha a $\vec{v}$ és az $\vec{\omega}$ által bezárt szög jele $\varphi$:
\[F_{\mathrm{Cor}}=2mv \omega \sin{\varphi}\]
Foucault 1851-es híres ingakísérletében az inga lengési síkja pont olyan ütember (32 órás periódusidővel) forgott körbe, amit a Coriolis-erős levezetés a 49. szélességi körön lévő Párizsra jósolt. Ezzel Foucault kísérletileg bizonytotta a Föld tengelyforgását.
A fenti egyenlet alapján a Coriolis-erő csak akkor lép fel, ha:
- a vonatkoztatási rendszer forog az inerciarendszerekhez képest (\(\vec{\omega}\) szögsebességgel)
- a test mozog a forgó vonatkoztatási rendszerben (\(\vec{v}\) sebességgel)
- a test \(\vec{v}\) sebességének és a vonatkoztatási rendszer \(\vec{\omega}\) szögsebességének van egymásra merőleges komponense
Nézzünk néhány speciális mozgás esetén a Coriolis-erőt!
1. Vízszintesen, észak-dél irányban mozgó test
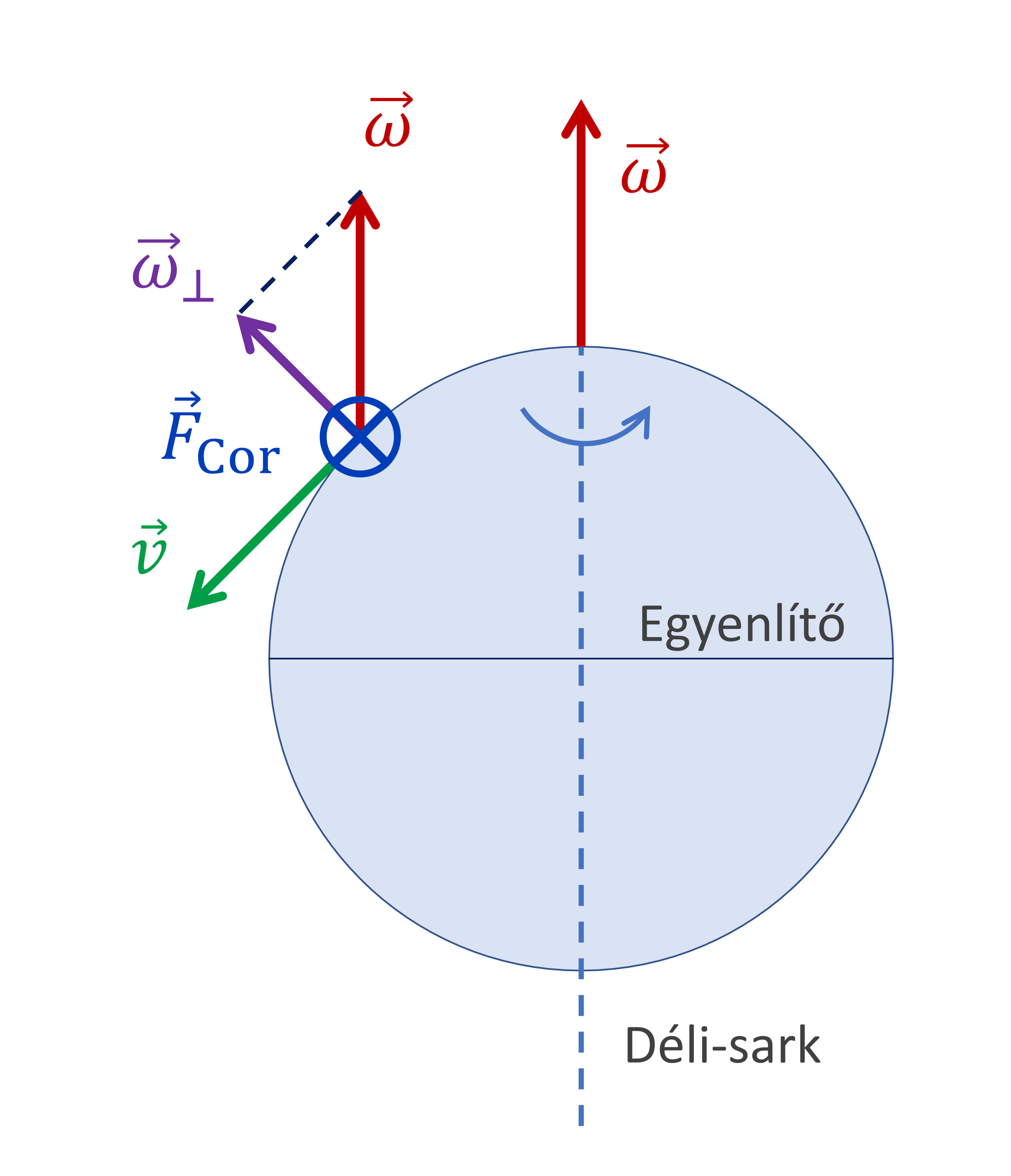
1.1 Az északi féltekén északi irányba mozgó test
Az északi féltekén a szögsebességvektornak a vízszintes sebességre merőleges komponense mindig a földfelszínhez képest függőlegesen felfelé mutat. Ha a test észak felé halad, akkor a Coriolis-erő keleti irányba hat (az ábrán a körben pötty, a vektor nyíl hegye néz felénk), azaz a menetirányhoz képest jobbra téríti el a testet:
1.2 Az északi féltekén déli irányba mozgó test
Ha a test az északi féltekén dél felé halad, akkor a Coriolis-erő nyugati irányba hat (az ábrán a körben X, a vektor nyilának végén a tollak néznek felénk), azaz a menetirányhoz képest szintén jobbra téríti el a testet:
Általában elmondható, hogy az északi féltekén a vízszintesen haladó testre mindig menetirány szerint jobbra eltérítő Coriolis-erő hat.
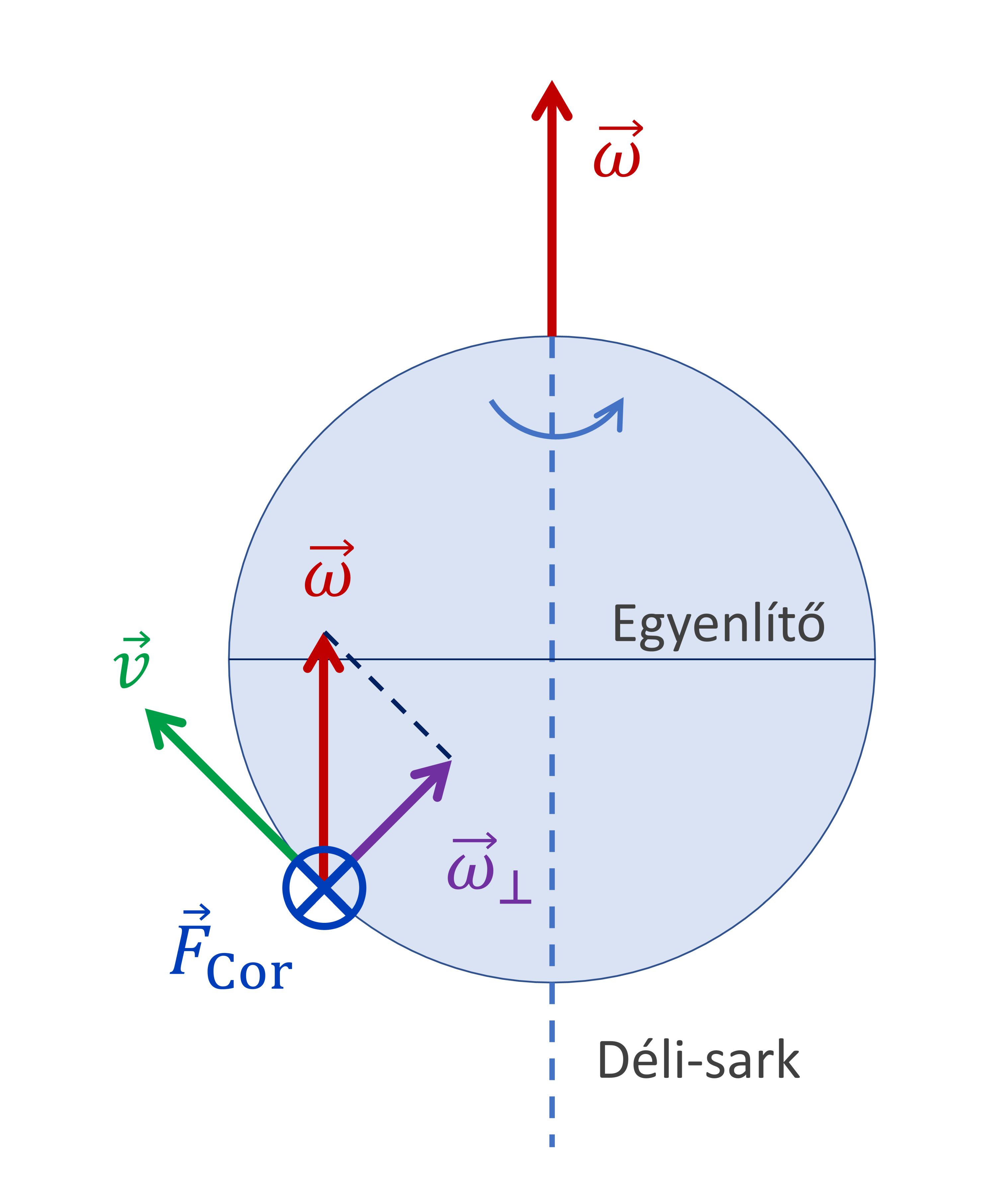
1.3 A déli féltekén északi irányba mozgó test
A déli féltekén észak-déli irányban mozgó testek esetén a szögsebességvektornak a sebességre merőleges komponense mindig függőlegesen lefelé (a Föld középpontja felé) mutat. Ha a test a déli féltekén észak felé halad, akkor a Coriolis-erő nyugati irányba hat, azaz a menetirányhoz képest balra téríti el a testet:
1.4 A déli féltekén déli irányba mozgó test
Ha a test a déli féltekén észak felé halad, akkor a Coriolis-erő keleti irányba hat, azaz a menetirányhoz képest szintén balra téríti el a testet:
Általában elmondható, hogy a déli féltekén vízszintesen mozgó testekre mindig a menetirány szerinti balra eltérító Coriolis-erő hat.
1.5 A pólusokon
A pólusokon nem tud északi vagy déli irányba haladni egy test. De mivel a vízszintesen haladó testet az északi féltekén mindenhol jobbra téríti el a Coriolis-erő, ezért az Északi-sarkon áthaladó testet is jobbra téríti el. A Déli-sarkon áthaladót pedig (bármilyen irányban is halad át a Déli-sarkon) balra téríti el a Coriolis-erő, ahogy az egész déli féltekén teszi.
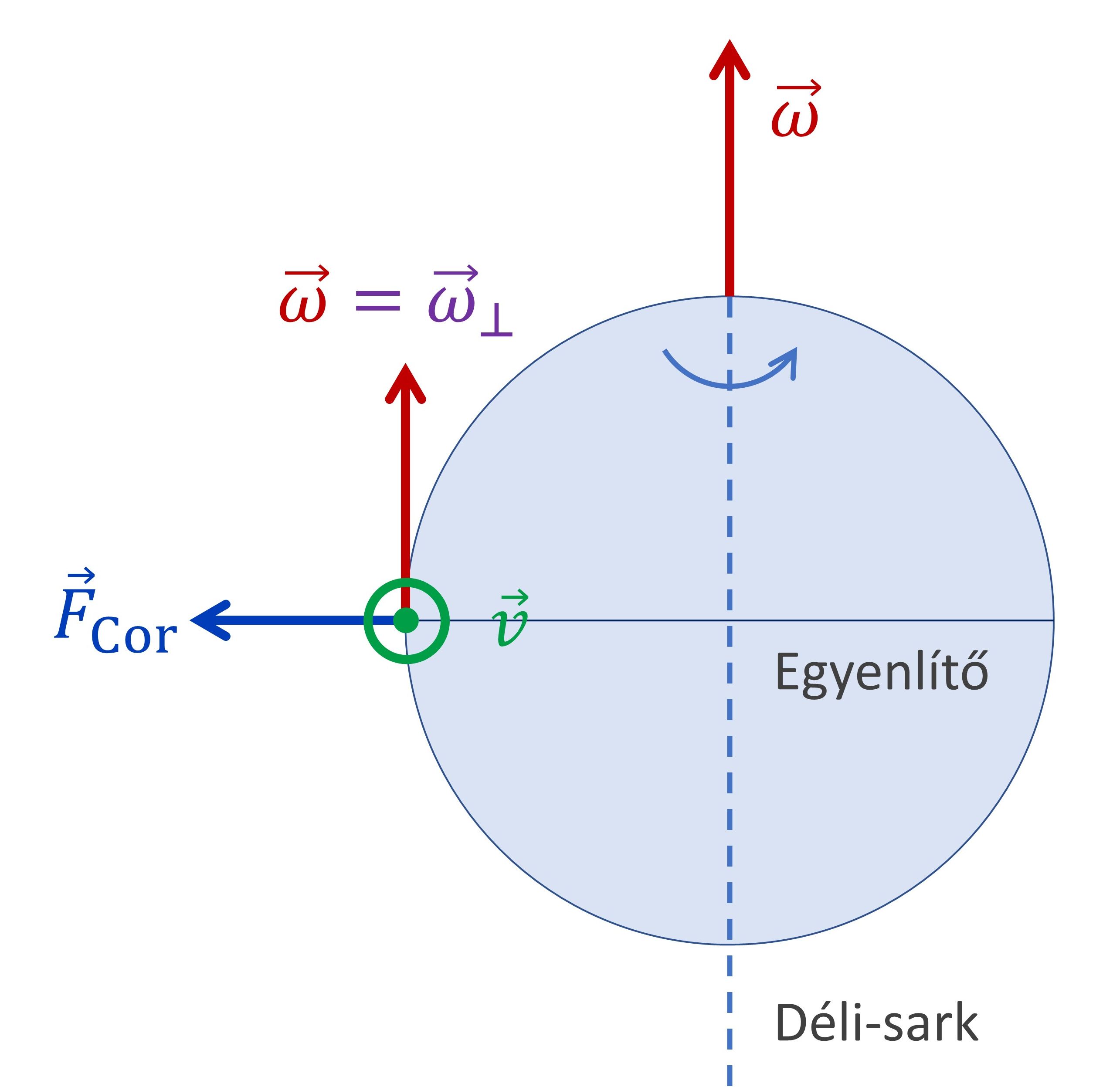
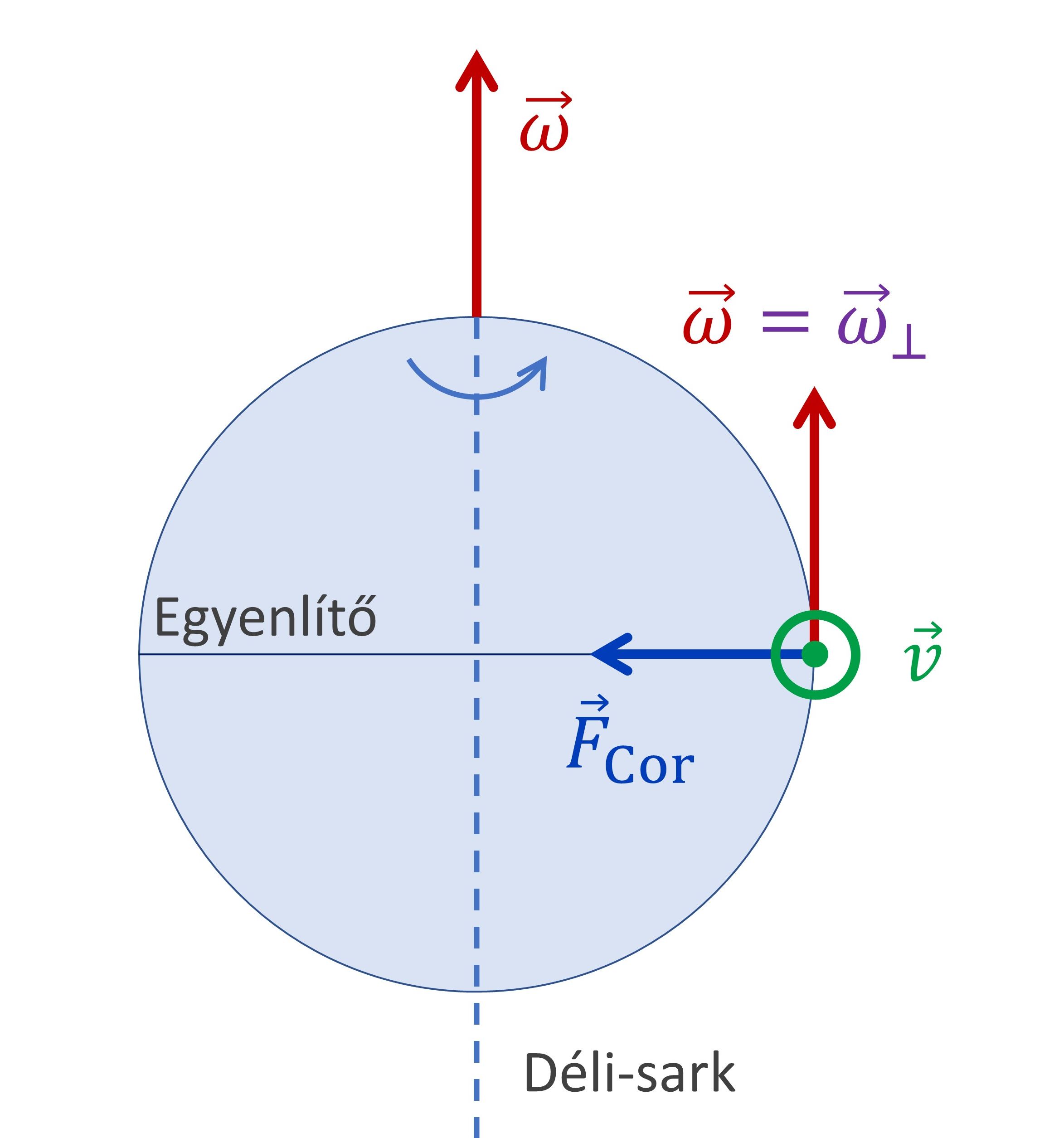
1.6 Az egyenlítőn északi illetve déli irányba haladó test
Ha az egyenlítőn északi vagy déli irányba halad a test, akkor a \(\vec{v}\) sebességvektora és a Föld \(\vec{\omega}\) szögsebességvektora párhuzamosak, így Coriolis-erő nem lép fel:
2. Vízszintesen, kelet-nyugati irányba haladó test
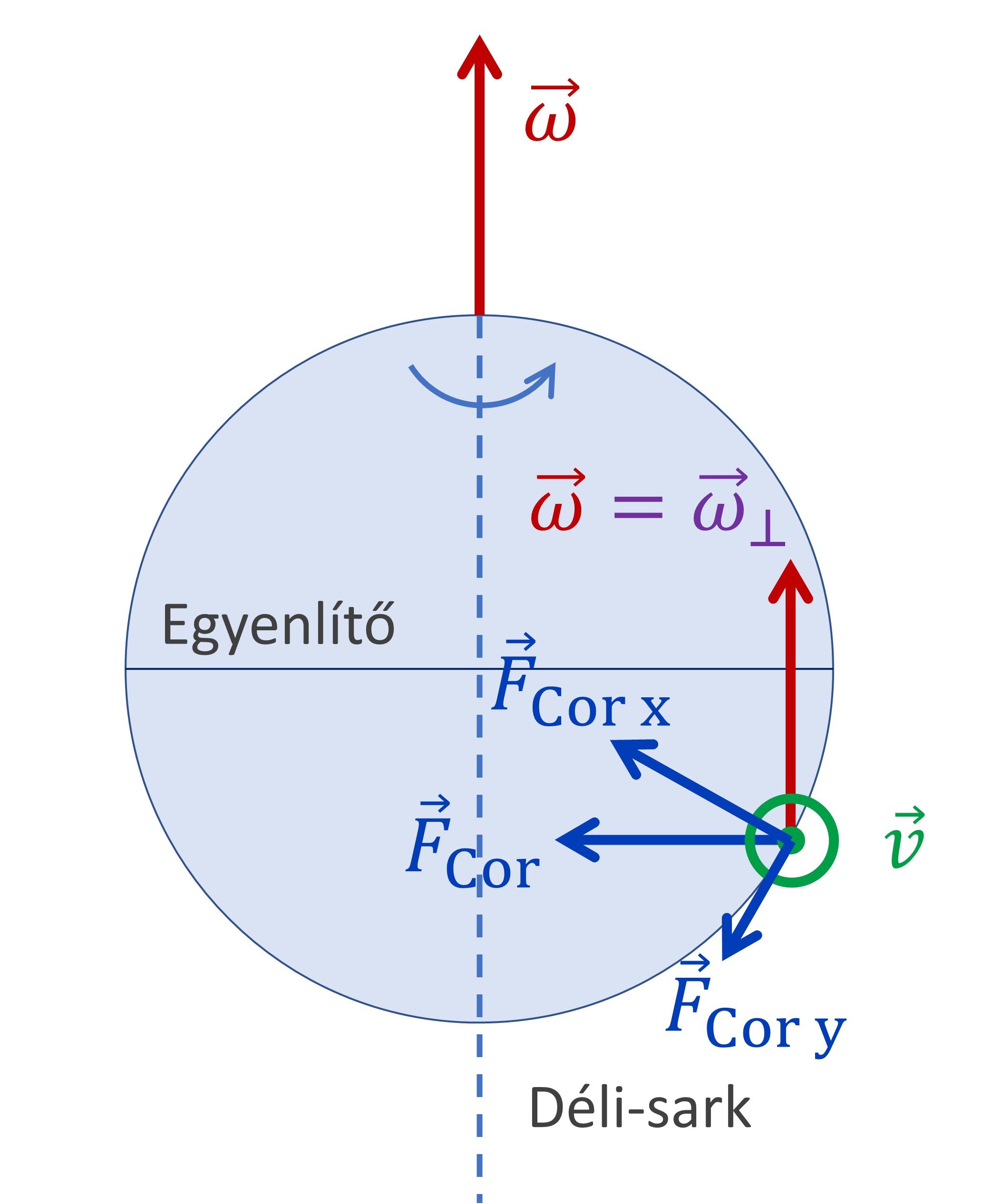
2.1 Az északi féltekén keleti irányba haladó test
Ilyenkor a Coriolis-erőnek lesz egy vízszintesen déli irányba ható komponense, és egy függőlegesen felfelé ható komponense:
2.2 Az északi féltekén nyugati irányba haladó test
Ilyenkor a Coriolis-erőnek lesz egy vízszintesen északi irányba ható komponense, és egy függőlegesen lefelé ható komponense:
2.3 A déli féltekén keleti irányba haladó test
Ilyenkor a Coriolis-erőnek lesz egy vízszintesen északi irányba ható komponense, és egy függőlegesen felfelé ható komponense:
2.4 A déli féltekén nyugati irányba haladó test
Ilyenkor a Coriolis-erőnek lesz egy vízszintesen déli irányba ható komponense, és egy függőlegesen lefelé ható komponense:
2.5 A pólusokon keleti, nyugati irányba haladó test
Ilyen nem lehetséges.
2.6 Az Egyenlítőn keleti irányba haladó test
Ilyenkor a Coriolis-erő függőlegesen felfelé hat, vagyis "emelőerőként" funkcionál:
2.7 Az Egyenlítőn nyugati irányba haladó test
Ilyenkor a Coriolis-erő függőlegesen lefelé hat, vagyis "lehúzóerőként" funkcionál:
3. Függőlegesen mozgó testre ható Coriolis-erő
3.1. Az északi féltekén felfelé mozgó test
Bla bla
3.2. Az északi féltekén lefelé mozgó test
Bla bla
3.3. A déli féltekén felfelé mozgó test
Bla bla
3.4. A déli féltekén lefelé mozgó test
Bla bla
4. A Coriolis-erő miatti eltérülés mértéke
Felmerülhet a kérdés, hogy a lassabban vagy a gyorsabban mozgó testet téríti-e el nagyobb mértékben a Coriolis-erő. Ehhez például haladjon egy test Budapesten keleti irányba, és nézzük a vízszintes eltérülését! Vízszintes eltérülést vízszintes erő tud okozni, vagyis a Coriolis-erőnek a vízszintes komponensét kell figyelembe vennünk, ahhoz viszont a vízszintesre merőleges szögsebességkomponens szükséges, tehát a függőlegesen felfelé mutató $\omega_{\bot}$. A Coriolis-erő vízszintes komponense déli rányba fog hatni.
Értelemszerűen hosszabb $s$ úton nagyobb $D$ eltérülés fog kialakulni, így értelmesebb az egységnyi $s$ útra első
$$\frac{D}{s}$$
eltérülést nézni. Számítsuk ezt ki!
A $v$ sebességgel kelet felé haladó test az $s$ utat
$$v=\frac{s}{t}$$
alapján
$$t=\frac{s}{v}$$
idő alatt teszi meg. Ugyan a Coriolis-erő elforgatja a sevességvektort, de ha csak rövid időtartamot nézünk, azalatt úgy vehetjük, hogy a $v$ sebességvektor csak lehanyagolható mértékben fordult el, vagyis a Coriolis-erő ezalatt állandó irányú. Állandó erő állandó gyorsulást okoz, ami miatt a megtett utat (a $D$ eltérülést) a négyzetes úttörvénnyel számíthatjuk:
$$D=\frac{a}{2}t^2$$
A Coriolis-erő okozta gyorsulás
$$F=m\cdot a$$
alapján
$$a=\frac{F_{\mathrm{Cor}}}{m}=\frac{2mv \omega}{m}=2v \omega$$
Ezt, és az időre kapott összefüggést beírva a négyzetes úttörvénybe:
$$D=\frac{a}{2}t^2$$
$$D=\frac{2v \omega}{2}\left(\frac{s}{v}\right)^2$$
$$D=\frac{ \omega s^2}{v}$$
Ebből az egységnyi $s$ útra jutó $D$ eltérülés:
$$\frac{D}{s}=\frac{\omega s}{v}$$
Vagyis az egységnyi útra eső eltérülés fordítottan arányos a $v$ sebességgel. Ennek a furcsa eredménynek a háttere az, hogy 2-szer nagyobb sebesség esetén ugyan 2-szer nagyobb a Coriolis-erő, ami nemcsak 2-szer nagyobb $a$ oldalirányú gyorsulást okoz, hanem azt is, hogy a test 2-szer rövidebb $t$ idő alatt fogja befutni az $s$ utat, márpedig a négyzetes úttörvény szerint az eltérülés az idő négyzetével arányos, így az időtartam feleződése 4-szeresen csökkkenti az eltérülést, míg a Coriolis-erő okozta gyorsulás csak 2-szeresre nő. Tömören: ugyan 2-szer nagyobb lesz az oldalirányú gyorsulás, de 4-szer rövidebb ideig fog érvényesülni, így fele akkora lesz az eltérülés.
5. Alkalmazások
5.1. A légáramlások furcsa irány
A földfelszín egyes területei eltérő hányadot nyelnek el a napsugárzásból, így az egyik terület jobban felmelegszik a másik területnél. Emiatt a földfelszín közelében különböző légnyomások alakulhatnak ki. Ha egy légtömeget az egyik oldalról nagyobb $p_1$ nyomás ér, mint a szemben lévő másik oldalról, akkor a nyomások miatt ébrefő $$F=p\cdot A$ erők különböznek, és az eredőjük a magasabb nyomású hely felől az alacsonyabb nyomású hely felé mutat (a negatív nyomásgradiens irányába).
Ilyenkor valamennyi levegő átáramlása az eltérő nyomású helyek között kiegyenlítheti a nyomáskülönbséget, amitől az imént még fennállt, légáramlást okozó hatás megszűnik. Ha szomszédos területek között nemcsak fennáll egy nyomáskülönbség, hanem az "folyamatosan újra is termelődik" (pl. elétrő mértékű folyamatos felmelegedés miatt), tehát egy kis átáramló levegő nem tudja megszüntetni a nyomáskülönbséget, olyankor azt gondolnánk, hogy a szél folyamatosan a magasabb nyomású hely felől fúj a kisebb nyomású hely felé. Csakhogy, a mozgó légtömegre Coriolis-erő is hat! Emiatt ha állandósul a szél sebessége, vagyis a levegőnek nincsen gyorsulása, az csak úgy lehetséges, hogy a levegőre ható erők eredője nulla. Két erő (a nyomáskülönbség miatti erő és a Coriolis-erő) csak úgy tudja kioltani egymást, ha azonos nagyságúak és elentétes irányúak. A nyomásülönbség miatti erő a nyomáscsökkenés felé mutat, így a Coriolis-erőnek a nyomásnövekedés irányába kell mutatnia. És mivel a Coriuolis-erő merőleges az áramló levegő sebességére, ezek csak úgy lehetségesek, ha a sebesség merőleges a nyomáskülönbség irányára.
5.2. A ágyúlövedékek
Az ágyúlövedékek is eltérülnek a Coriolis-erő miatt. Ez csak nagy távolságra tüzeléskor jelentős effektus.