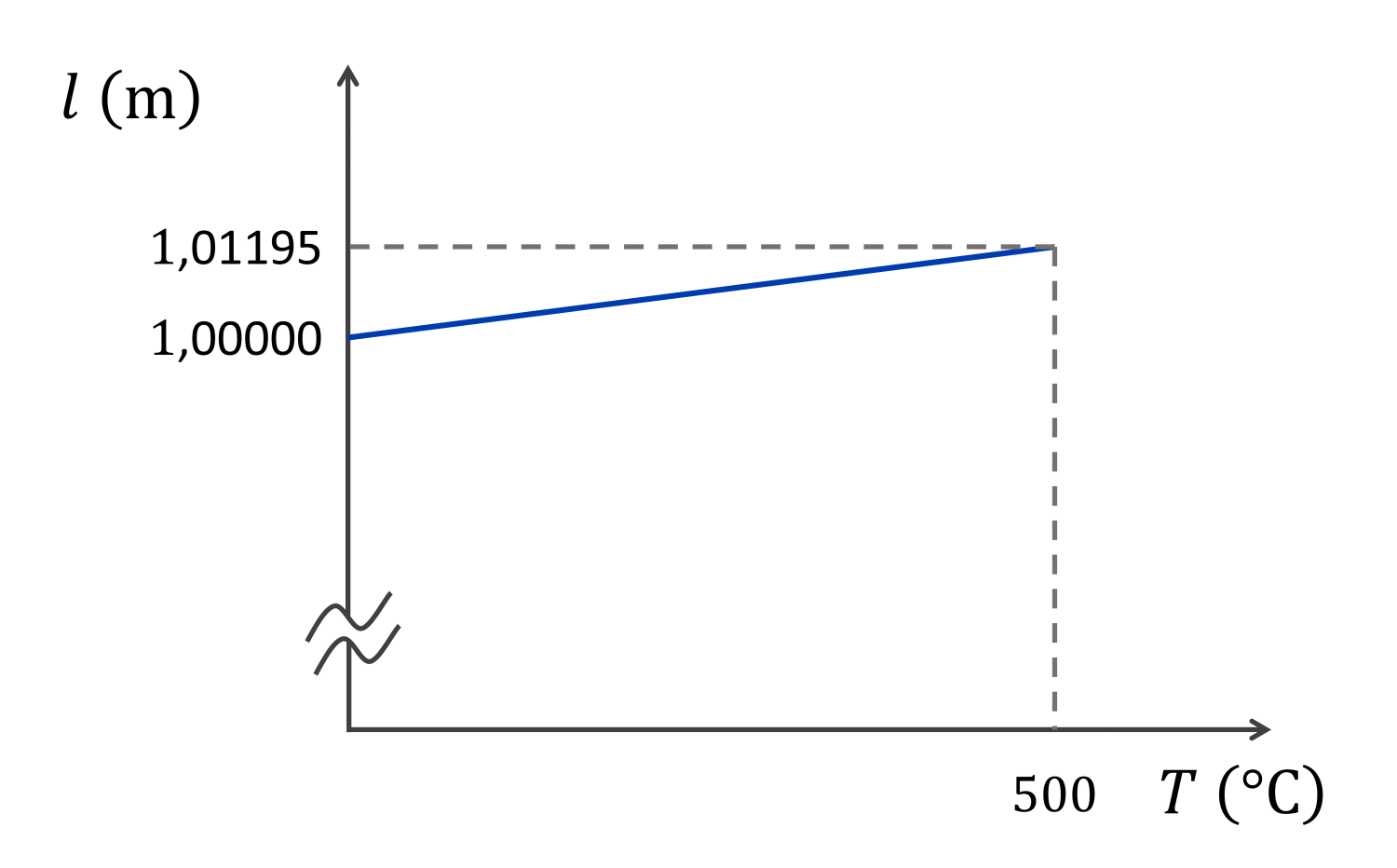
A tapasztalat szerint egy rúd hosszának hőmérséklettől való függvényének képe mindig (nem origón átmenő) egyenes:
Mi következik ebből? Hogy a függvény meredeksége állandó. Nézzük meg a hőtágulási törvényt, hogy abból milyen meredekség adódik!
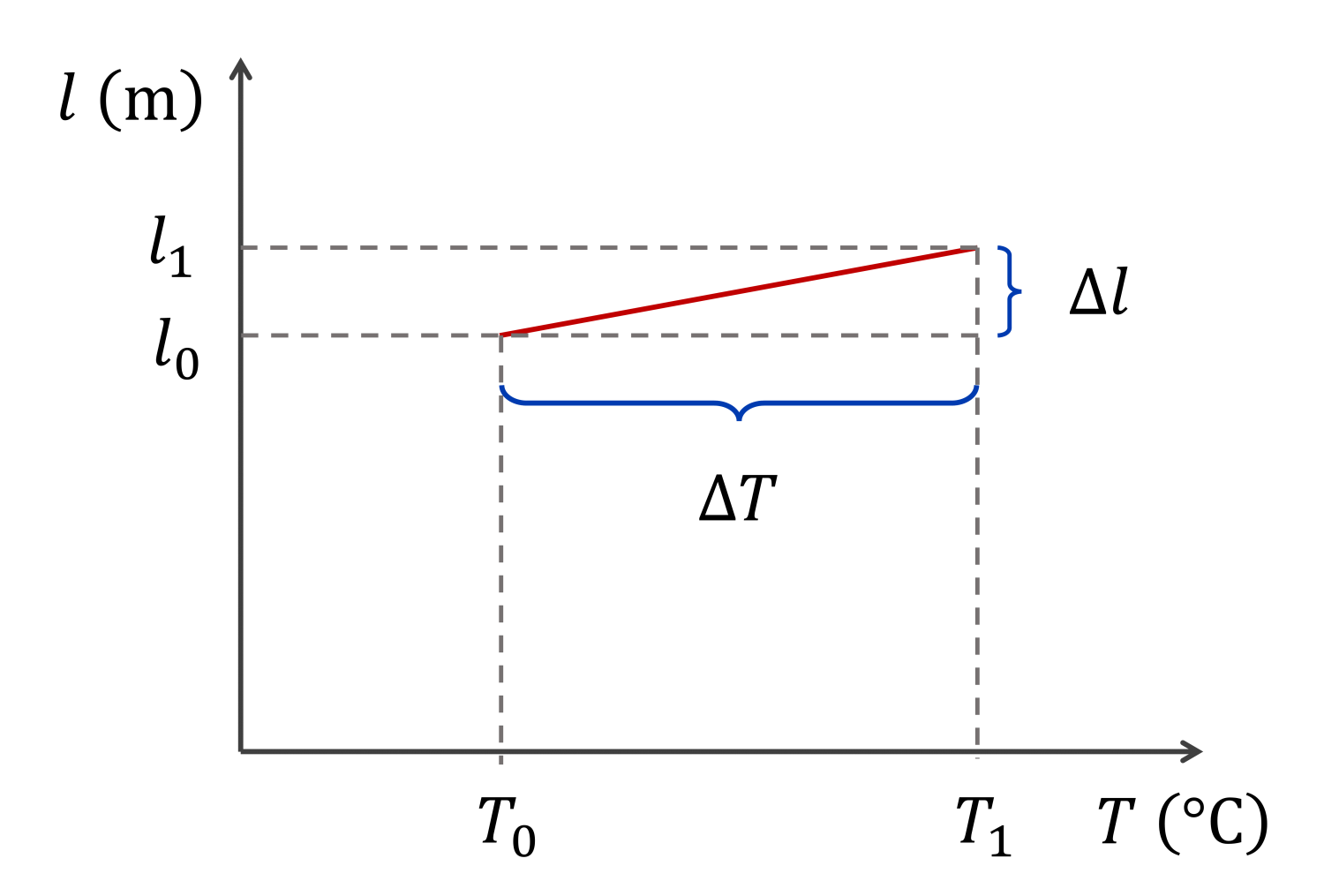
A meredekség általában azt jelenti, hogy egységnyi x-tengelyen vett változás hatására mekkora változás következik be az y-tengelyen mért értékben:
\[m=\frac{\Delta y}{\Delta x}\]
Vagyis a mi esetünkben, mivel a függőleges tengelyen a rúd $l$ hosszát ábrázoljuk, a vízszintesen pedig a $T$ hőmérsékletet:
\[m=\frac{\Delta l}{\Delta T}\]
Rendezzük ki ezt a kifejezést a lineáris hőtágulási törvényből:
\[\Delta l=l_0\cdot \alpha \cdot \Delta T\]
\[m=\frac{\Delta l}{\Delta T}=l_0\cdot \alpha \]
Azt kaptuk tehát, hogy az $l_0\cdot \alpha $ kifejezés állandó (mivel ez a hőtágulási görbe egyenesének meredeksége). Vagyis a lineáris hőtágulási törvényben szereplő $\alpha $ együttható nem állandó, hanem a hőmérséklettel változnia kell, hiszen ha különböző hőmérsékletekről kezdjük a melegítést, akkor különböző az \(l_0\) kezdeti hossz is.
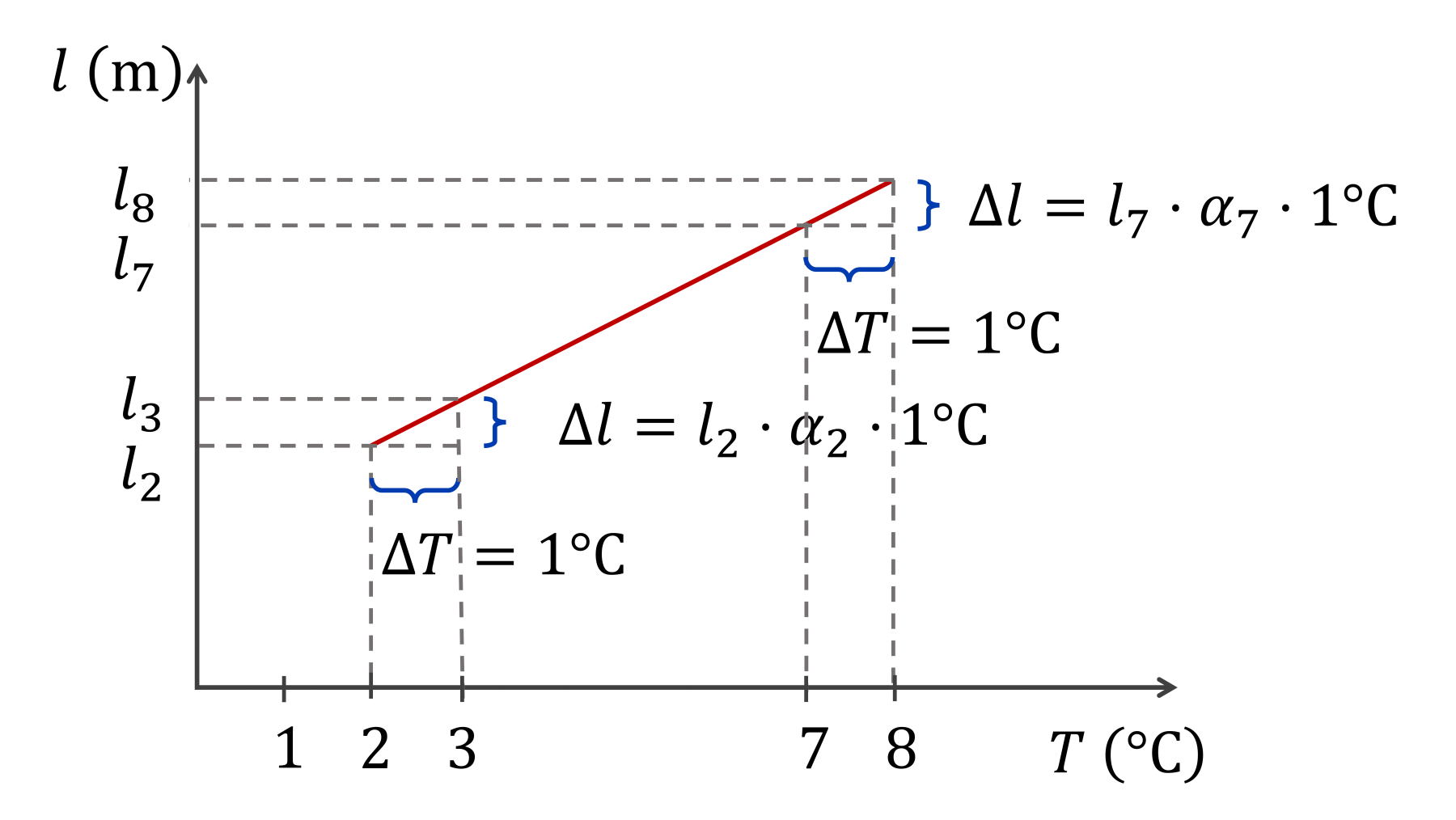
A fenti képen az egyszerűség kedvéért egységnyi hőmérsékletnövekedéssel melegítünk, először \(2\ \mathrm{{}^\circ C}\)-ról, aztán \(7\ \mathrm{{}^\circ C}\)-ról. Mivel a tágulási grafikon egyenes, ezért ugyanakkora jobbra lépésre ugyanakkora felfelé lépésnek kell bekövetkeznie. Mivel a törvény szerint a hosszváltozások
\[\Delta l=l_0\cdot \alpha \cdot \Delta T\]
A két folyamatban az \(l_0\) kezdeti hosszok egyértelműen eltérőek, ezért a \(2\ \mathrm{{}^\circ C}\)-ról induló folyamat kezdeti hosszát jelöljük \(l_2\)-vel, a \(7\ \mathrm{{}^\circ C}\)-ról induló folyamat kezdeti hosszát pedig \(l_7\)-tel. Így:
\[\Delta l=l_2\cdot \alpha \cdot \Delta T\]
\[\Delta l=l_7\cdot \alpha \cdot \Delta T\]
Ha a bal oldalak azonosak, akkor a jobb oldalaknak is azonosnak kell lenniük, amiből:
\[l_2\cdot \alpha \cdot \Delta T=l_7\cdot \alpha \cdot \Delta T\]
Ez viszont csak úgy lehetséges, ha az \(\alpha\) hőtágulási együtthatók is eltérőek. Ezért meg kell őket különböztetnünk az alsó indexben:
\[l_2\cdot \alpha_2 \cdot \Delta T=l_7\cdot \alpha_7 \cdot \Delta T\]
Általában azt írhatjuk, hogy a hosszváltozás:
\[\Delta l=l_0\cdot \alpha_0 \cdot \Delta T=l_1\cdot \alpha_1 \cdot \Delta T=l_{\mathrm{X}}\cdot \alpha_{\mathrm{X}} \cdot \Delta T\]
Emiatt a komolyabb táblázatokban a hőtágulási együtthatóhoz mindig odaírják, hogy az milyen kiindulási hőmérsékletre érvényes. Például:
Hogyan változik az \(\alpha\) a hőmérséklet növekedésével? Mivel melegítéskor az $l_0$ kezdeti hossz egyre nő, ezért az $\alpha $ egyre csökken.
Az \(\alpha \) hőmérsékletfüggésének következménye néhány hőtágulással kapcsolatos furcsaság, melyeket gyakran (tévesen) azzal szoktak magyarázni, hogy a hőtágulási függvény a valóságban nem tökéletesen egyenes, hanem eltér attól (kissé elhajlik, elgörbül), pedig a furcsaságok tökéletes egyenes esetén is fennállnak. Ezen a furcsaságok tárgyalása itt található.